Свойства линейного коэффициента корреляции

1. Линейный коэффициент корреляции может принимать значения в пределах от –1 до +1.

2. Если 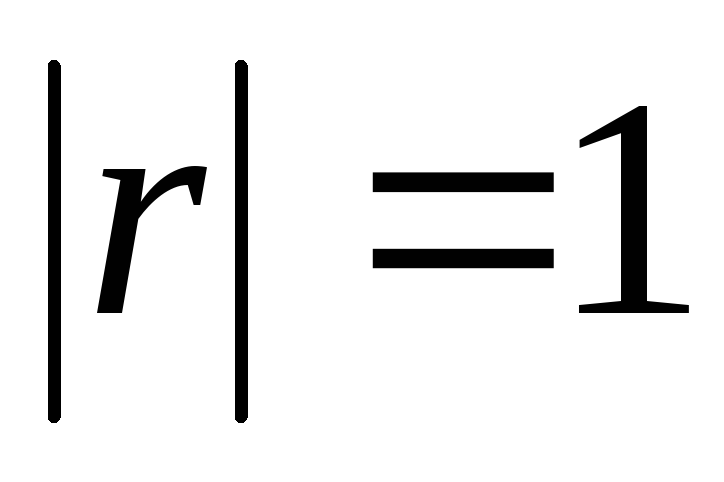, то связь между признаками функциональная, т. е. на результативный признак влияет только рассматриваемый факторный признак и больше ничего, еслиr = 0, то связь между признаками отсутствует.

3. Если r > 0, то связь между признаками прямая, еслиr < 0, то связь – обратная.

4. Выделяют следующие промежутки для r:

связь между признаками фактически отсутствует;

связь слабая;

связь умеренная;

связь сильная.

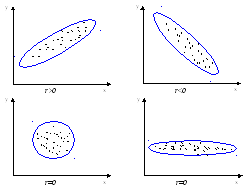
Рис. 2.Примеры расположения точек на графике и значений коэффициента корреляции

Для оценки существенности линейного коэффициента корреляцииrиспользуютt– критерий Стьюдента. При этом выдвигается гипотеза о равенстве коэффициента корреляции нулю.

Проверка гипотезы:

1. Вычисляют фактические значения t-критерия дляr:

(такая формула применяется при небольшом объеме выборки).

2. По таблице t-распределения Стьюдента с учетом принятого уровня значимост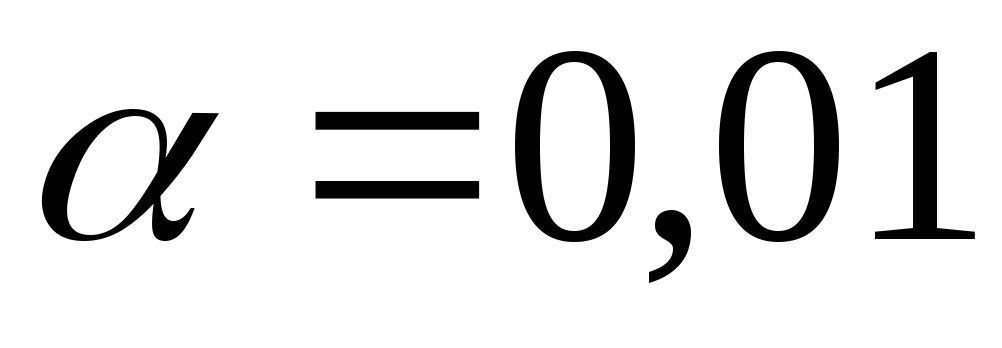иили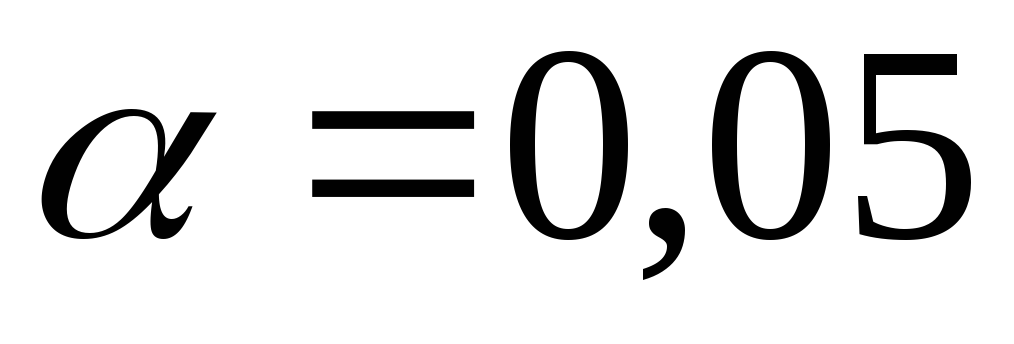и числе степеней свободы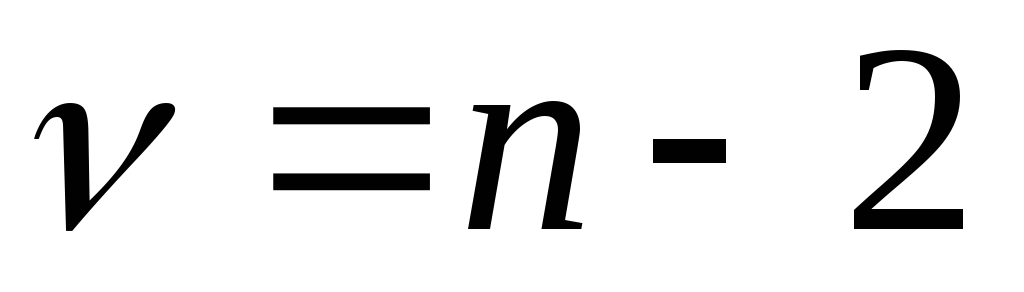определяют.

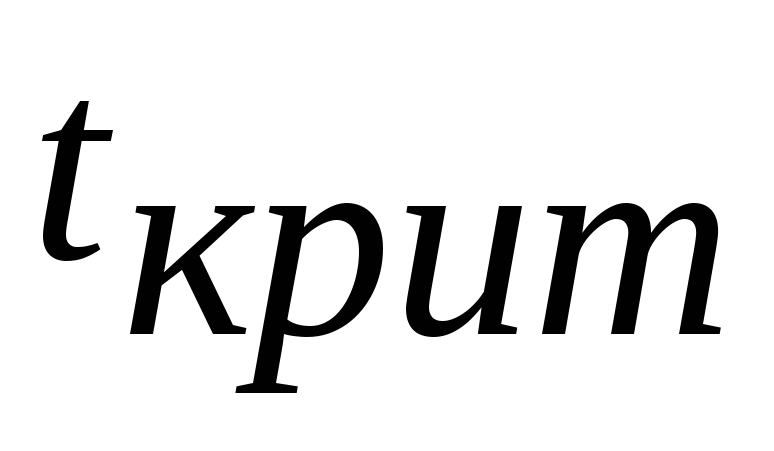3. Если 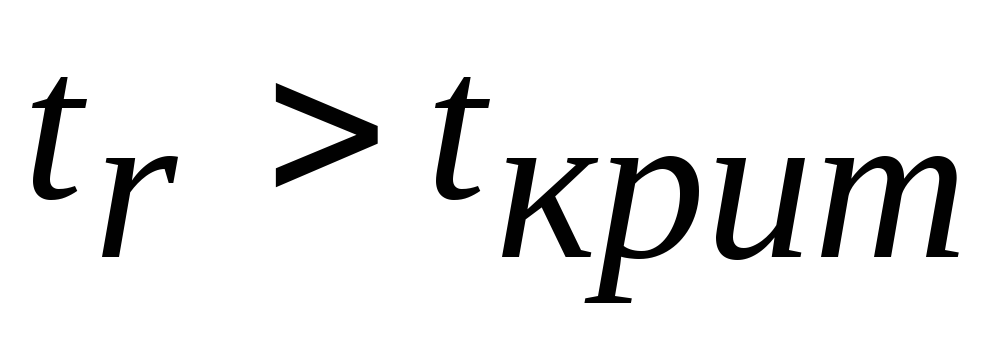, то гипотеза отвергается, что свидетельствует о значимости коэффициента корреляции.

Корреляционное отношениеопределяется по формулам:

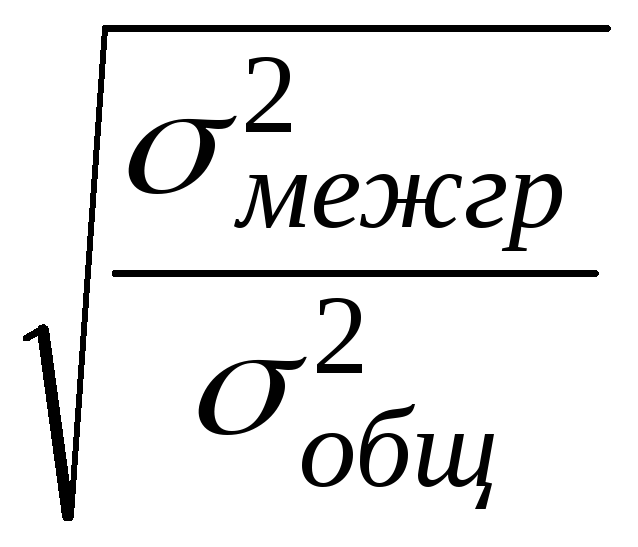η = илиη = ,

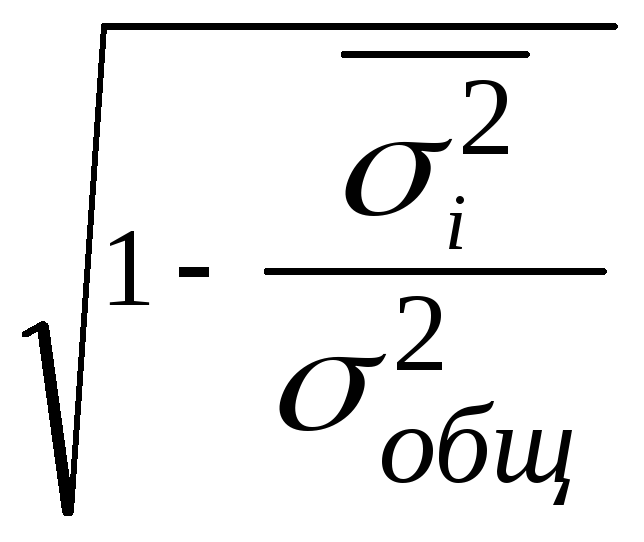где – межгрупповая дисперсия результативного признака, вызванная влиянием признака-фактора;

– общая дисперсия результативного признака;

– средняя из внутригрупповых дисперсий результативного признака.

Вычисление корреляционного отношения требует достаточно большого объема информации, которая должна быть представлена в форме групповой таблицы или в форме корреляционной таблицы, т. е. обязательным условием является группировка данных по признаку-фактору.

По несгруппированным данным эмпирическое корреляционное отношение может быть рассчитано по следующей формуле:

.

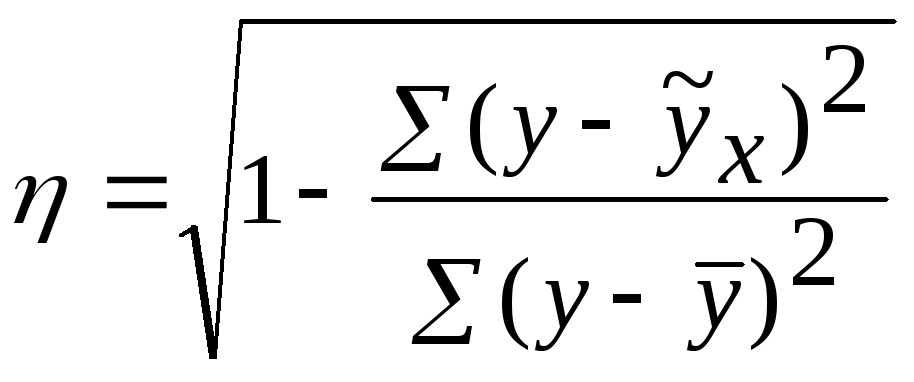где y– эмпирические (фактические) значения результативного признака;

– среднее значение результативного признака;

– выравненные значения результативного признака, вычисленные по аналитическому уравнению.

Корреляционное отношение в квадрате (), а для парной связи линейный коэффициент корреляции в квадрате () называюткоэффициентом детерминации(причинности), он отражает долю факторной дисперсии в общей дисперсии.

Коэффициент детерминации(D) показывает, на сколько процентов изменение среднего значения результативного признака определяется влиянием данного факторного признака.

В практике могут быть использованы и другие показатели для определения степени тесноты связи.

Элементарной характеристикой степени тесноты связи является коэффициент Фехнера:

,

где n_a – количество совпадений знаков отклонений индивидуальных величин факторного признакахи результативного признакауот их средней арифметической величины (например, «плюс» и «плюс», «минус» и «минус», «отсутствие отклонения» и «отсутствие отклонения»);

n_b – количество несовпадений знаков отклонений индивидуальных значений признаков от значения их средней арифметической.

Коэффициент Фехнера используют при небольшом объеме исходной информации. Он изменяется в пределах от –1 до 1.

Для определения тесноты связи как между количественными, так и между качественными признаками, при условии, что значения этих признаков можно проранжировать по возрастанию или убыванию, используется коэффициент корреляции рангов Спирмэна:

,

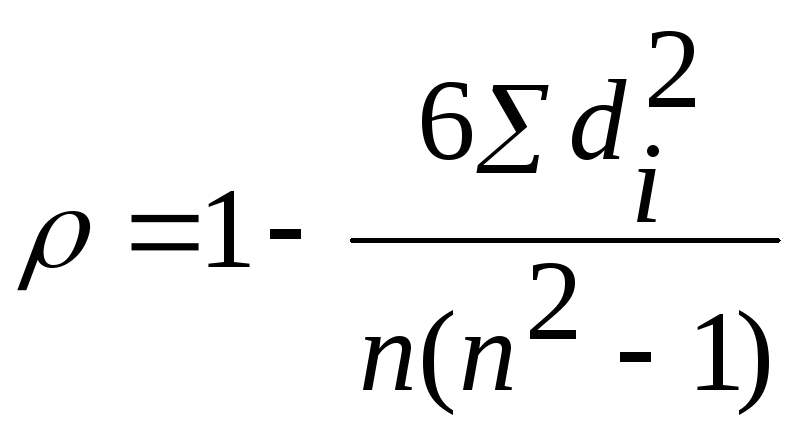где d_i – разность между величинами рангов признака-фактора и результативного признака;

n– число показателей (рангов) изучаемого ряда.

Он варьирует в пределах от –1 до 1.