Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока :

η_э 0,1-0,3 0,3-0,5 0,5-0,7 0,7-0,9 0,9-0,99

Сила связи Слабая Умеренная Заметная Тесная Весьма тесная

4. Показатели формы распределения

Для получения приблизительного представления о форме распределения строят графики распределения (полигон и гистограмму). В практике статистических исследований приходится встречаться с самыми различными распределениями. Однородные совокупности характеризуются, как правило, одновершинными распределениями. Многовершинность свидетельствует о неоднородности изучаемой совокупности. В этом случае необходима перегруппировка данных с целью выделения более однородных групп.

Выяснение общего характера распределения предполагает оценку степени его однородности, а также исчисление показателей асимметрии и эксцесса.

Ряды распределения могут иметь один и тот же центр группирования (показатели центра распределения) и одинаковые пределы варьирования признака (показатели вариации), однако при этом отличаться характером распределения единиц совокупности вокруг центра. Если большая часть совокупности расположена левее центра, имеет место левосторонняя асимметрия, если правее – правосторонняя.

Для оценки степени асимметричности применяют моментный и структурный коэффициенты асимметрии.

Моментный коэффициент асимметрии определяется по формуле:

А_S = 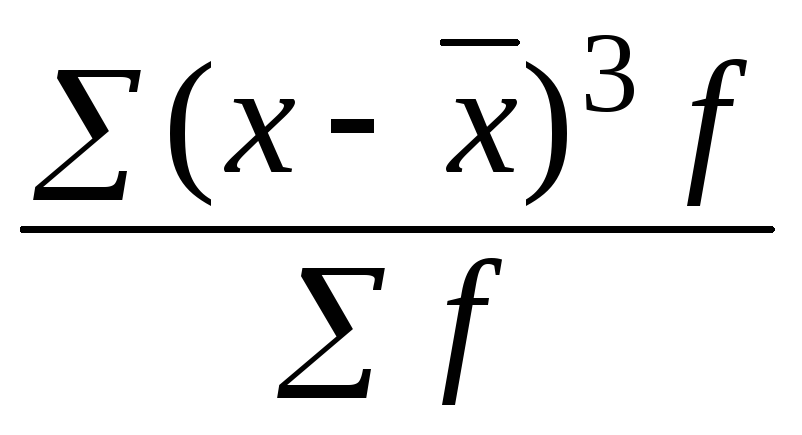: σ³.

На направление асимметрии указывает знак коэффициента: если А_S<0, то это левосторонняя асимметрия (ее называют также отрицательной асимметрией), при правосторонней (положительной) асимметрии А_S >0, если А_S = 0 – распределение симметричное. Чем больше абсолютная величина коэффициента, тем больше степень скошенности.

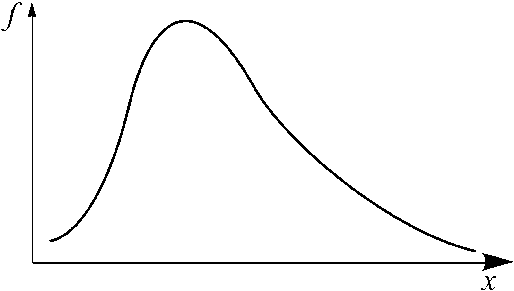
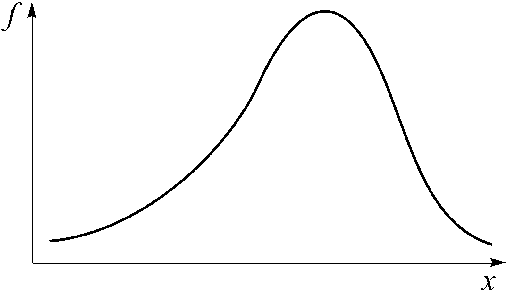
Рис. 2. А_S<0 левосторонняя асимметрия Рис. 3. А_S >0 правосторонняя асимметрия

Степень существенности асимметрии можно оценить с помощью средней квадратической ошибки коэффициента асимметрии, которая зависит от объема изучаемой совокупности и рассчитывается по формуле:

=,

где п – число единиц в совокупности.

Если отношение > 3, асимметрия считается существенной и распределение признака в генеральной совокупности не является симметричным, если < 3, то асимметрия признается несущественной, вызванной влиянием случайных обстоятельств.

Структурные показатели асимметрии характеризуют асимметричность только в центральной части распределения, т. е. основной массы единиц, и в отличие от моментного коэффициента не зависят от крайних значений признака. Наиболее часто применяют структурный коэффициент асимметрии, предложенный английским статистиком К. Пирсоном:

А_S = .

В симметричном распределении Для симметричных распределений рассчитывается показатель эксцесса (островершинности):

Е_Х = (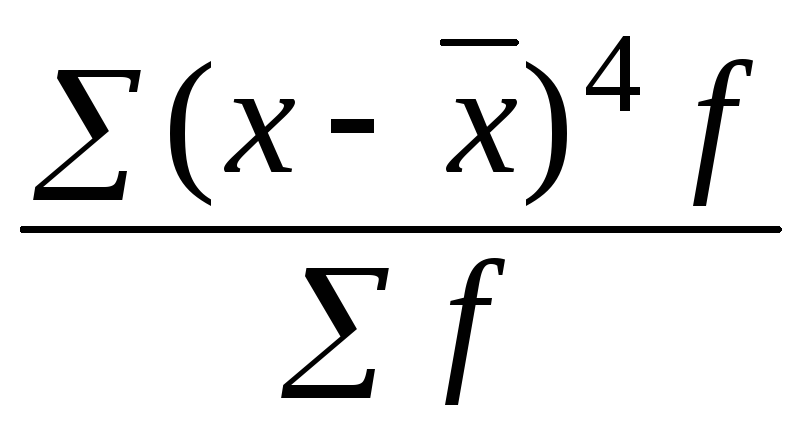: σ⁴) – 3.

Эксцесс может быть положительным и отрицательным. У островершинных распределений показатель эксцесса имеет положительный знак (+), а у плосковершинных – отрицательный знак (–). Предельным значением отрицательного эксцесса является значение Е_Х = –2; величина положительного эксцесса может быть величиной бесконечной. В нормальном распределении Е_Х = 0.

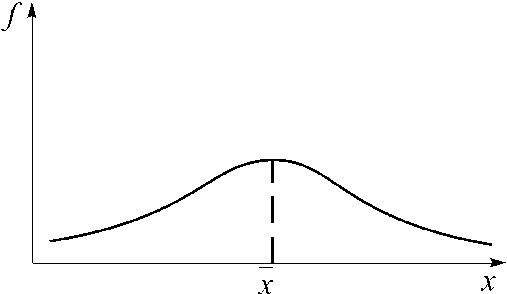
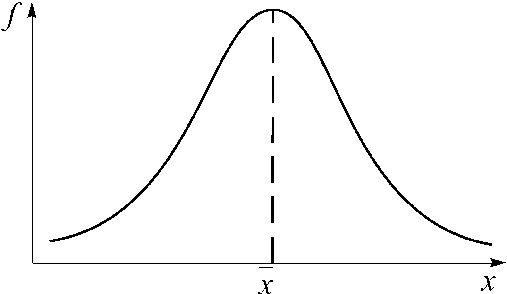
Рис. 4. Е_Х < 0 плосковершинное распределение Рис. 5. Е_Х > 0 островершинное распределение

Средняя квадратическая ошибка эксцесса исчисляется по формуле:

=

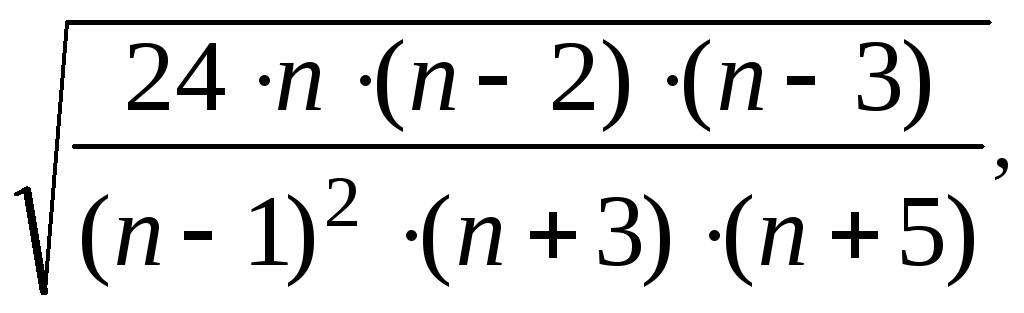
где п – число наблюдений.

Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное эмпирическое распределение к типу кривых нормального распределения. Уравнение нормальной кривой:

,

где y_t – ордината кривой нормального распределения;

t – нормированное отклонение, равное ;

– арифметическая средняя распределения;

– математические константы.

Рис. 6.Кривая нормального распределения

Нормальная кривая имеет огромное значение в теории выборочного метода, поскольку может быть показано, что средние стандартные отклонения, рассчитанные по случайным выборкам, тяготеют к нормальным в случае больших размеров выборок, если даже совокупность, из которой они взяты, сама не является нормально распределенной.

Особенности кривой нормального распределения:

1. кривая симметрична относительно максимальной ординаты, которая соответствует , ее величина равна ;

2. кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности. При этом, чем больше значения отклоняются от , тем реже они встречаются;

3. равновероятны одинаковые по абсолютному значению, но противоположные по знаку отклонения значений переменной хот :

а) кривая имеет две точки перегиба, находящиеся на расстоянии от ;

б) в промежутке (приt= 1) находится 68,3% всех значений признака; в промежутке (приt= 2) находится 95,4% всех значений признака; в промежутке (приt= 3) – 99,7% всех значений признака.