Элементарная математика / Ponarin-I

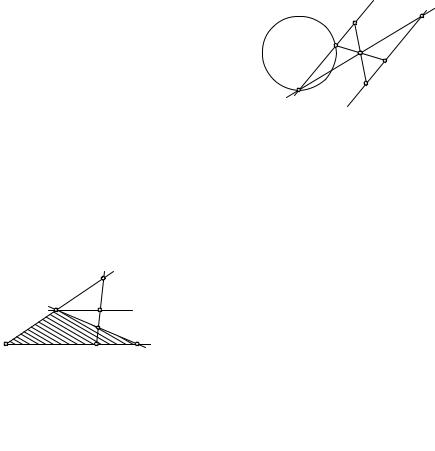
гонали, и потому является прямоугольником. Точки A, N, M, C, Q, P лежат на одной окружности с центром O. Поэтому BAD = 1/2 NOP . Для того, чтобы прямоугольник MNP Q был квадратом, необходимо и достаточно, чтобы NOP = 90◦, т. е. чтобы BAD = 45◦ (при условии, что указанные в задаче перпендикуляры проведены через вершины A

иC острых углов данного параллелограмма).

За д а ч а 3. Через данную точку A провести прямую так, чтобы ее отрезок с концами на данных прямой и окружности делился точкой пополам.

Р е ш е н и е. Пусть m и a — данные прямая и окружность, CD — ис-

комый отрезок, C m, D a (рис.8). Тогда ZA(C) = D. Если ZA(m) = m1,

(рис.9). Проведем через P произвольную прямую MN, M a, N b. Для определенности будем полагать, что MP < P N. Построим прямую a1, симметричную a относительно P . Пусть b ∩ a1 = B, a1 ∩ (MN) = K, (P B) ∩ a = A. Тогда площадь треугольника OAB меньше площади треугольника OMN. В самом деле, треугольники AMP и BKP равны,

так как они симметричны относительно точ-

Nки P . Но SOAB = SOMPB + SAMP = SOMPB +

bP аналогично получим тот же результат. По-

скольку прямая MN произвольная, а пря- O a M A мая AB вполне определенная для данного

Рис. 9

угла и данной точки P , то треугольник OAB

имеет наименьшую возможную площадь из всех треугольников, отсекаемых от угла прямыми, проходящими через P . Из этого анализа следует способ построения искомой прямой AB: нужно построить a1 = ZP (a), тогда точка B = a1 ∩ b определяет прямую (AB) = (BP ). Искомая прямая всегда существует и единственна.

161

Задачи на доказательство

1.01.Через диаметрально противоположные точки A и B окружности проведены параллельные хорды AC и BD. Докажите, что отрезок CD — диаметр этой окружности.

1.02.Точки E и F — середины параллельных сторон AD и BC соответственно параллелограмма ABCD. Докажите, что прямые BE и F D делят диагональ AC на три равные части.

1.03.Дан четырехугольник ABCD с прямыми углами A и C. Докажите, что точки ZA(D) и ZC(D) симметричны относительно ортоцентра H треугольника ABC.

1.04.Через точки, делящие медианы треугольника в отношении 1 : 2, считая от вершин, проведены прямые, параллельные соответственным сторонам этого треугольника. Докажите, что треугольник с вершинами

вточках пересечения этих прямых равен данному треугольнику.

1.05.В треугольник вписана окружность и проведены касательные к ней параллельно сторонам треугольника. Докажите, что в полученном шестиугольнике противоположные стороны равны.

1.06.В четырехугольнике ABCD угол B равен углу D, а диагональ AC делится другой диагональю пополам. Докажите, что данный четырехугольник — параллелограмм.

1.07.Точка O — центр параллелограмма ABCD. Докажите, что центры окружностей, вписанных в треугольники AOB, BOC, COD, DOA, являются вершинами ромба. В каком случае этот ромб будет квадратом?

1.08.На сторонах параллелограмма вне его построены правильные треугольники. Докажите, что их центры являются вершинами параллелограмма.

1.09.Дан параллелограмм ABCD и произвольная точка M. Через вершины A, B, C, D проведены прямые, параллельные соответственно прямым MC, MD, MA, MB. Докажите, что построенные прямые пересекаются в одной точке.

1.10.Даны две параллельные прямые и прямой угол с вершиной O в центре симметрии этих прямых. Докажите, что расстояние от точки O до прямой, соединяющей точки M и N пересечения данных прямых со сторонами угла, не зависит от выбора стороны угла.

1.11.Докажите, что точки, симметричные ортоцентру треугольника относительно середин его сторон, лежат на описанной около треугольника окружности.

Задачи на построение

1.12. Внутри угла с вершиной O дана точка M. Постройте прямую OM, не используя точку O.

162

1.13.Постройте центр данного параллелограмма, не используя его вершины.

1.14.Постройте квадрат, если дан его центр и две точки, принадлежащие прямым, которые содержат две противоположные стороны квадрата.

1.15.Через точку пересечения двух данных окружностей проведите прямую, на которой эти окружности отсекают равные хорды.

1.16.Постройте параллелограмм, у которого две противоположные вершины находятся в данных точках, а две другие — на данной окружности.

1.17.Даны четыре попарно непараллельные прямые и не принадлежащая им точка O. Постройте параллелограмм с центром O, вершины которого лежат по одной на данных прямых.

Задачи для внеклассной работы

1.18.Двое игроков кладут на прямоугольный стол пятаки, которые разрешается класть лишь на свободные места. Проигрывает тот, кто не может сделать очередной ход. Докажите, что игрок, кладущий пятак первым, всегда может выиграть.

1.19.От пункта A к пункту B, находящемуся на острове, требуется провести телефонную связь. Как, не переплывая реку, определить необходимую длину телефонного кабеля?

1.20.Противоположные стороны шестиугольника параллельны и равны. Докажите, что этот шестиугольник имеет центр симметрии.

1.21.Докажите, что отрезки, соединяющие середины противоположных сторон четырехугольника, и отрезок с концами в серединах его диагоналей пересекаются в одной точке и делятся ею пополам.

1.22.На окружности даны четыре точки. Через середину каждого из отрезков с концами в двух данных точках проводятся перпендикуляры

кпрямой, содержащей две оставшиеся точки. Докажите, что построенные шесть перпендикуляров пересекаются в одной точке.

1.23.В окружности даны две произвольные хорды AB и CD. На хорде CD задана точка P . Найдите на окружности такую точку M, чтобы прямые AM и BM высекали на хорде CD отрезок, делящийся точкой P пополам.

1.24.Через общую точку двух окружностей проведите прямую так, чтобы эти окружности высекали на ней хорды, разность которых равна данному отрезку a.

1.25.В треугольнике ABC проведены медианы AM и CK. Углы BAM и BCK равны 30◦. Докажите, что треугольник ABC правильный.

163

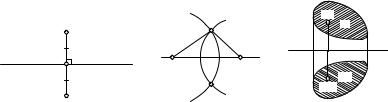
1.26.Дан треугольник ABC и точка P . Точки P1, P2, P3 — ее ортогональные проекции на прямые BC, CA, AB соответственно. Точки Q1, Q2, Q3 симметричны точкам P1, P2, P3 относительно середин отрезков BC, CA, AB. Докажите, что перпендикуляры к прямым BC, CA и AB в точках Q1, Q2 и Q3 соответственно пересекаются в одной точке.

§3. Осевая симметрия

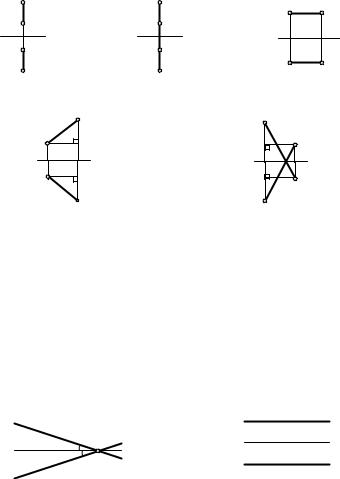
3.1.Определение и свойства осевой симметрии плоскости. Точки M

иM1 называются симметричными относительно заданной прямой l, если эта прямая является серединным перпендикуляром к отрезку MM1 (рис. 10). Каждая точка прямой l симметрична сама себе. Преобразование плоскости, при котором каждая точка отображается на сим-

метричную ей точку относительно данной прямой l, называется осевой симметрией с осью l и обозначается Sl : Sl(M) = M1.

Точки M и M1 взаимно симметричны относительно l, поэтому Sl(M1) = M. Следовательно, преобразование, обратное осевой симметрии, есть та же осевая симметрия: Sl−1 = Sl, Sl ◦ Sl = E. Иначе говоря, осевая симметрия плоскости является инволютивным преобразованием (12◦).

Образ данной точки при осевой симметрии можно просто построить, пользуясь только одним циркулем. Пусть l — ось симметрии, A и B — произвольные точки этой оси (рис. 11). Если M / l и Sl(M) = M1, то по свойству точек серединного перпендикуляра к отрезку имеем: AM = AM1 и BM = BM1. Значит, точка M1 принадлежит двум окружностям: окружности с центром A радиуса AM и окружности с центром B радиуса BM (M — данная точка).

Фигура F и ее образ F1 при осевой симметрии называются симмет-

Теорема. Осевая симметрия плоскости есть движение.

164

Если A и B — любые точки плоскости и Sl(A) = A1, Sl(B) = B1 то надо доказать, что A1B1 = AB. Предлагаем это сделать читателю, руководствуясь рис. 13—17.

Из сравнения ориентаций треугольника и его образа получаем, что осевая симметрия плоскости есть движение второго рода.

На основании теоремы п. 1.2 осевая симметрия отображает каждую прямую на прямую. В частности, каждая из прямых, перпендикулярных оси симметрии, отображается этой симметрией на себя.

Теорема. Прямая, отличная от перпендикуляра к оси симметрии, и ее образ при этой симметрии пересекаются на оси симметрии или ей параллельны.

Д о ка з а т е л ь с т в о. Пусть дана прямая, не перпендикулярная оси l симметрии. Если m ∩l = P и Sl(m) = m1, то m1 6= m и Sl(P ) = P , поэтому P m1 (рис. 18). Если же m k l, то m1 k l, так как в противном случае согласно доказанной первой части этой теоремы прямые m и m1 пересекались бы в точке прямой l, что противоречит условию m k l (рис.19).

m

m

l

lP

165

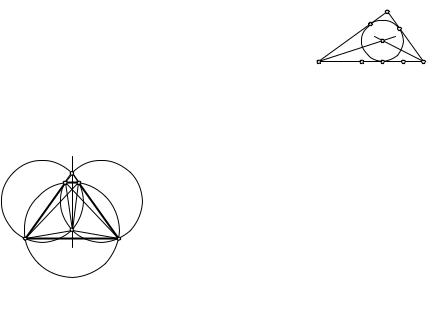
В силу определения равных фигур, прямые, симметричные относительно прямой l, образуют с прямой l равные углы (рис. 18).

Прямая l называется осью симметрии фигуры F , если при симметрии с осью l фигура F отображается на себя: Sl(F ) = F . Говорят, что фигура F симметрична относительно прямой l.

Например, всякая прямая, содержащая центр окружности, является осью симметрии этой окружности. Действительно, пусть M — произвольная точка окружности w с центром O, O l, Sl(M) = M1. Тогда Sl(O) = O и OM1 = OM, т. е. M1 w. Итак, образ любой точки окружности принадлежит этой окружности. Следовательно, Sl(w) = w.

Осями симметрии пары непараллельных прямых служат две перпендикулярные прямые, содержащие биссектрисы углов между данными прямыми. Осью симметрии отрезка является содержащая его прямая,

атакже серединный перпендикуляр к этому отрезку.

3.2.Решение задач с помощью осевой симметрии. Рассмотрим наиболее типичные ситуации применения осевой симметрии в задачах.

З а д а ч а 1. Точки M и N симметричны вершине C треугольника ABC относительно прямых, содержащих бис-

нами BC и CA (рис. 20). Так как биссектриса

угла принадлежит его оси симметрии и AT = AP , BQ = BP , то точка P служит образом точек Q и T при указанных осевых симметриях.

Поскольку CQ = CT , то и MP = NP .

SЗ а д а ч а 2. Продолжения боковых сторон

жит центр окружности, описанной около трапеции. Далее, ASM =

=BSM `AM = `MC AM = MC. Так как, кроме того, AM =

=MB и DM = MC, то точка M равноудалена от всех вершин трапеции.

166

167

точке P , пересекаясь с прямыми a и b, дает точки A и B. Касательная в одной из этих точек пересекает прямую c в третьей искомой точке C. Исследование опускаем.

Задачи на доказательство

1.27.Даны две концентрические окружности. Через две точки этих окружностей, лежащие на одной прямой с центром, проведена произвольная окружность. Докажите, что две другие точки пересечения ее с данными окружностями также коллинеарны с центром.

1.28.Окружность, концентричная с вписанной в треугольник окружностью, пересекает прямые, содержащие его стороны, соответственно в парах точек A и B, C и D, E и F . Докажите, что AB = CD = EF .

1.29.Если ортоцентр треугольника совпадает с центром вписанной

внего окружности, то треугольник правильный. Докажите.

1.30.Если ортоцентр треугольника совпадает с его центроидом, то треугольник правильный. Докажите.

1.31.Точки A, B, C лежат на одной прямой. Точка M не принадлежит этой прямой. Докажите, что окружности с диаметрами MA, MB, MC имеют еще одну общую точку.

1.32.Докажите, что точки, симметричные ортоцентру треугольника относительно прямых, содержащих его стороны, лежат на описанной около треугольника окружности.

1.33.Если H — ортоцентр треугольника ABC, то окружности, описанные около треугольников HAB, HBC, HCA, равны. Докажите.

1.34.Докажите, что точки, симметричные ортоцентру треугольника относительно прямых, содержащих его стороны, являются вершинами треугольника, биссектрисы которого лежат на тех же прямых, что и высоты данного треугольника.

1.35.На биссектрисе внешнего угла C треугольника ABC взята точка M 6= C. Докажите, что MA + MB > CA + CB.

Задачи на построение

1.36.С помощью построений определите расстояние от данной точки на стороне угла до его вершины, если эта вершина недоступна.

1.37.Через данную точку проведите прямую, пересекающую две данные прямые под равными углами.

1.38.На плоскости даны непараллельные прямые a и b. Постройте прямую, перпендикулярную третьей данной прямой m и пересекающую прямые a и b в точках, равноудаленных от m.

1.39.Постройте квадрат, две противоположные вершины которого лежали бы на данной прямой, а две другие — на данных окружностях.

168

1.40.Дана прямая a и точки M и N в полуплоскости с границей a. Найдите на прямой a такую точку P , чтобы сумма MP + NP была наименьшей.

1.41.Постройте четырехугольник ABCD, у которого диагональ AC принадлежит биссектрисе угла A, если известны все стороны четырехугольника.

1.42.Постройте треугольник по двум сторонам и разности противолежащих им углов.

1.43.Постройте треугольник по стороне, разности двух других сторон и углу, заключенному между данной стороной и большей из двух других.

Задачи для внеклассной работы

1.44.Точка M лежит на диаметре AB окружности. Хорда CD проходит через M и пересекает AB под углом 45◦. Докажите, что сумма CM2 + DM2 не зависит от выбора точки M.

1.45.В окружности, центр которой не указан, проведены две параллельные неравные хорды. Разделите эти хорды пополам, пользуясь только одной линейкой.

1.46.Даны две пересекающиеся прямые. Постройте циркулем и линейкой оси симметрии этих прямых, пользуясь циркулем только два раза.

1.47.Через точку, лежащую вне данной прямой, проведите при помощи циркуля и линейки прямую, параллельную данной, пользуясь циркулем только два раза.

1.48.Дана прямая m, не принадлежащая ей точка M и окружность a

водной полуплоскости с границей m. Найдите на данной прямой такую точку P , чтобы сумма расстояния MP и длины отрезка касательной из точки P к окружности была наименьшей.

1.49.Даны прямая m и окружность a. Найдите на прямой m такую точку X, чтобы прямая m и одна из касательных, проведенных к окружности a через точку X, были симметричны относительно другой касательной.

1.50.Дорога AB пересекает под острым углом реку BC. Гонец находится в точке P внутри угла ABC. Его конь хочет пить, а гонец спешит выехать на дорогу AB. В каком месте реки гонец должен напоить коня, чтобы скорее попасть на дорогу?

1.51.Постройте треугольник по данным серединам двух его сторон и прямой, на которой лежит биссектриса угла, противолежащего одной из этих двух сторон.

169

1.52.Постройте треугольник по стороне, соответствующей ей высоте

иразности углов, прилежащих к данной стороне.

1.53.Постройте четырехугольник ABCD, в который можно вписать окружность, зная стороны AB и AD и углы при вершинах B и D.

1.54.На прямоугольном бильярде ABCD находятся два шара M

иN. Как надо толкнуть шар M, чтобы он, отразившись от бортов AB

иBC, попал в шар N?

1.55.Дан острый угол с вершиной O и внутри него точки P и Q. Постройте треугольник ABC такой, что AC = BC, сторона AB принадлежит одной стороне угла, вершина C — другой, а стороны AC и BC содержат точки P и Q.

§4. Перенос

4.1.Определение и свойства переноса. Переносом Tr— плоскости на заданный вектор r¯ называется преобразование плоскости, которое каждую точку M отображает на такую точку M0, что MM0 = r¯.

Это определение оправдано тем, что отображение, удовлетворяющее указанным в нем двум требованиям, отображает плоскость на себя

иобратно, т. е. является преобразованием плоскости (5◦).

Перенос Tr— полностью характеризуется своим вектором r¯. Очевидно, перенос на нулевой вектор является тождественным преобразованием:

T—0 = E. Преобразование, обратное переносу Tr—, есть перенос на противоположный вектор: (Tr—)−1 = T−r—.

Теорема. Перенос есть движение.

Д о к а з а т е л ь с т в о. Если Tr—(M) = M0 и Tr—(N) = N0, то MM0 =

= NN0 = r¯. Следовательно, MM0 + M0N = M0N + NN0, или MN = M0N0

ние отображает прямую на прямую. Если M и N — две различные точки прямой a и Tr—(M) = M0, Tr—(N) = N0, то MN = M0N0 (рис. 25), откуда следует Tr—(a) k a. Соответственные лучи этих прямых сонаправлены.

Обратно, если движение отображает каждый луч на сонаправленный с ним луч, то оно является переносом. Действительно, пусть при

170