
ЭКОНОМЕТРИКА и математическая экономика / Эконометрика. Учебник продвинутый (2005)
.pdf2.2. Средние величины |
53 |
В качестве z0 и zN |
естественно принять, соответственно, 2x1 − z1 |
и 2xN − zN −1 , так что первое и последнее значение в ряде наблюдений оказываются в точности на середине своих полуинтервалов. Относительные частоты для всех полуинтервалов одинаковы и равны 1 N . Однако плотность частоты различается: она тем выше, чем короче полуинтервал, т.е. чем плотнее наблюдения расположены на числовой оси.
2.2. Средние величины
Средние величины, или просто средние, являются особым подклассом интенсивных величин, т.к. рассчитываются как отношения других величин. Они выступают наиболее общими характеристиками совокупности объектов. Каждая средняя рассчитывается по конкретному признаку, характеризующему объекты совокупности, и является качественно такой же величиной, имеет те же единицы измерения или ту же размерность (или она безразмерна), что и усредняемый признак. Характер средних по объемным и относительным величинам несколько различается. Ниже рассматриваются сначала средние объемные и на их примере — виды средних, затем — средние относительные величины.
Пусть xi — некоторый объемный признак i-го объекта, 1, . . . , N , то есть
количество объектов в совокупности равно N , как и прежде, x = xi , тогда
i
расчет среднего по совокупности значения данного объемного признака, который обычно обозначается тем же символом, но без индекса объекта и с чертой над символом, осуществляется по следующей формуле:
x¯ = |
1 |
x = |
1 |
xi. |
|
N |
|||
|
N |
i |
||
|
|
|
|
|
Это — среднее арифметическое (среднеарифметическое) простое или средняя арифметическая (среднеарифметическая) простая. Оно является отношением двух объемных величин: суммарного по совокупности признака и количества объектов в совокупности.
Пусть теперь вся совокупность делится на k групп, Nl — количество объектов в l-й группе, N = Nl , значение признака внутри каждой группы не варьируется
l
и равняется xl . Тогда |
|
|
|
|
|||
x¯ = |
1 |
Nlxl = |
αlxl, где αl = |
Nl |
, |
αl = 1 — вес l-й группы. |
|
N |
N |
||||||
|
l |
l |
|
|
|||
|
|
|
|
|
|||
Это — среднее арифметическое (среднеарифметическое) взвешенное (среднеарифметическая взвешенная).
54 |
Глава 2. Описательная статистика |
Каналогичной формуле для средней по исходной совокупности можно придти
ииначе. Пусть, как и сначала, признак варьирует по всем объектам совокупности, а x¯l — среднеарифметическое простое по l-й группе. Очевидно, что
x = Nl x¯l, и x¯ = αlx¯l.
По такой же формуле производится расчет средней по данным эмпирического распределения частот признака (см. предыдущий пункт). В качестве x¯l в таком случае принимают не среднее по l-й группе, а, как отмечалось выше, середину l-го полуинтервала.
Предполагая, что все объекты совокупности имеют разные веса (вес i-го объекта равен αi ), среднее по совокупности записывается как взвешенное:
|
|
|
x = |
αixi. |
Это — более общая |
формула среднеарифметического: при равных весах, |
|||
то есть в случае, если αi |
= 1 |
N |
для всех i, она преобразуется в формулу средне- |
|
|
|
|
|
|
арифметического простого.
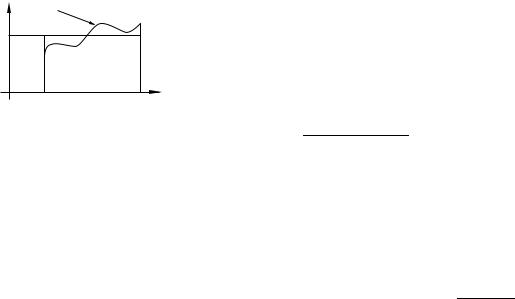
Для нахождения средней величины типа запаса за некоторый период времени используется среднее арифметическое взвешенное, называемая средним хронологическим (или средней хронологической). Смысл этой величины поясняется
рисунком 2.7. |
|
||
|
x |
x(t) |
|
_ |
E |
C |
|
|
|
||
x |
|
|
|
|
F |
|
|
|
|
|
|
|
B |
|
|
|
A |
D |
t |
|
|
Рис. 2.7 |
|
Среднюю хронологическую x¯ надо найти так, чтобы площадь ABCD под линией динамики x(t) (BC), т.е. сумма значений показателя за период, равнялась площади прямоугольника AEF D под линией средней EF (см. рис. 2.7).
Другими словами, для расчета средней хронологической используется формула:
x¯ = площадь ABCD . длина AD
На практике в дискретном случае этот расчет можно провести следующим об-
разом. |
|
Пусть x0, x1, . . . , xN — значения некоторой объемной величины типа запаса |
|
в моменты времени t0, t1, . . . , tN , и τi = ti − ti−1, i = 1, . . . , N , τ = τi |
|
(длина AD). |
|
Если предположить, что на каждом временном отрезке τi динамика показателя |
|
линейна, то его суммарное значение на этом отрезке рассчитывается как τi xi + xi−1 |
, |
2 |
|

2.2. Средние величины |
55 |
и для общей средней хронологической справедливо соотношение:
1 N
x¯ = 2τ i=1 τi (xi + xi−1).
В выражении этой величины как среднеарифметической взвешенной веса име-
ют следующие значения: |
|
|
|
|
||
α0 = |
τ1 |
, αi = |
τi + τi+1 |
, i = 1, . . . , N − 1, αN = |
τN |
|
|
|
|
. |
|||
2τ |
2τ |
2τ |
||||
Их сумма равна единице. |
||
Если все временные отрезки τi одинаковы, то веса первого и последнего x |
||
в средней хронологической будут равняться 1 2N , а веса всех промежуточных |
||
«x-ов» — 1 |
N |
. |
|
|
|
На практике чаще всего рассчитывают средние величины типа запаса за период времени (обычно за год) по данным на начало и конец этого периода (года). Т.е. решается задача нахождения средней хронологической x¯ за некоторый период, для которого известно значение показателя на начало — x0 и конец периода — x1 . Эта величина, чаще всего, находится как средневзвешенное арифметическое:
x¯ = (1 − α) x0 + αx1, или x¯ = x0 + α∆, или ∆ = x1 − x0.
Если динамика показателя равномерна (линейна), то α = 1 2 ; если более интенсивные сдвиги в величине показателя происходят в 1-й половине периода, то α > 1 2 ; в противном случае — α < 1 2 . В советской статистике при расчете, например, среднегодовых основных фондов α принимался в интервале от 0.3 до 0.4, поскольку в плановой экономике вводы и выбытия фондов обычно сдвигаются к концу года — к моменту отчета по плану. Этот параметр иногда называют
среднегодовым коэффициентом.
При предположении, что на данном отрезке времени неизменным остается относительный прирост (моментный темп прироста), и динамика имеет экспоненциальный характер, справедливы следующие выражения (как и прежде, τ — длина данного временного отрезка, ∆ — прирост показателя за период):
xt = x0 |
|
x1 |
|
t τ |
при 0 t τ , |
|
|
|
|||
|
|
, |
|
|
|
||||||
|
x0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
τ |
|
|
t |
τ |
x1 − x0 |
|
∆ |
|
|
|
|
|
|
|
|
|
|||||
x¯ = |
|
|
|
x1 |
dt = |
= |
. |
||||
|
|
|
|
|
|
|
ln 1 + ∆ x0 |
||||
|
τ |
0 |
|
|
x0 |
|
ln x1 − ln x0 |
|
|||

56 |
Глава 2. Описательная статистика |
В знаменателе этого выражения для средней хронологической находится непрерывный темп прироста за период (см. п. 1.8), т.е. средняя хронологическая определяется делением абсолютного прироста на относительный прирост за период. Это — особый вид средней, которую иногда и называют собственно хронологической.
Чтобы лучше понять ее смысл, полезно найти ее предельное значение при ∆ → 0. Для этого логарифм в знаменателе раскладывается в степенной ряд:
ln 1 + |
∆ |
= |
∆ |
− |
∆ |
2 1 |
+ |
∆ |
3 1 |
− |
∆ |
4 1 |
+ · · ·, |
|||
x0 |
x0 |
x0 |
|
2 |
x0 |
|
4 |
x0 |
|
4 |
||||||
затем сокращается ∆ в числителе и знаменателе, и он (∆) приравнивается нулю. Искомый предел равен x0 . Таким образом, на бесконечно малых отрезках времени значение этой величины равно самому показателю, а на конечных отрезках — его среднему значению при предположении, что темп роста на этом отрезке остается неизменным.
Возвращаясь к общему случаю N + 1 временной точки, среднюю хронологическую при предположении неизменности темпа роста внутри каждого временного периода можно рассчитать следующим образом:
x¯ = |
1 |
N |
xi − xi−1 |
τi. |
|
||||
|
τ i=1 ln xi − ln xi−1 |
|||
Несложно убедиться в том, что в случае, если средние в единицу времени темпы
|
|
1 |
|
|
|
|
||
роста |
xi |
|
τi на всех временных отрезках одинаковы и равны среднему в едини- |
|||||
|
||||||||
|
xi−1 |
1 |
|
|||||
|
|
|
|
|
xN |
τ |
||
цу темпу роста за весь период |
|
, среднее хронологическое рассчитывается |
||||||
x0 |
||||||||
|
|
|
|
|
|
|
||
только по двум крайним значениям: |
|
|
||||||
|
|
|
|
x¯ = |
xN − x0 |
. |
||
|
|
|
|
|
|
ln xN − ln x0 |
||
Расчет средних хронологических величин типа запаса является необходимой операцией для приведения этих величин к форме, сопоставимой с величинами типа потока, имеющими другое качество. Так, например, производительность труда рассчитывается как отношение выпуска продукции за определенный период времени к средней хронологической занятых в производстве за этот же период. Если величины типа запаса и потока имеют одно качество (потоки выражают изменение запасов за период времени), то используются и показатели отношения потока к запасу на начало или конец периода (или наоборот). Так, например, отношение
2.2. Средние величины |
57 |
выбывших в течение года основных фондов к основным фондам на начало года называется коэффициентом выбытия фондов, а отношение годового ввода фондов к фондам на конец года — коэффициентом обновления фондов.
Среднеарифметическое является частным случаем так называемого среднестепенного или среднего степенного, которое рассчитывается по следующей формуле:
x¯ = |
1 |
αixik k . |
Следует обратить внимание, что эта величина существует не при всех k, если некоторые из xi отрицательны. Чтобы избежать непринципиальных уточнений, в дальнейшем предполагается, что все значения признака положительны.
При k = 1 среднее степенное превращается в обычное среднеарифметическое, при k = 2 это — среднеквадратическое, используемое для оценки степени вариации признака по совокупности, при k = −1 — среднее гармоническое, примеры использования которого приводятся при рассмотрении средних относительных величин, при k = 0 — среднее геометрическое.
Последнее утверждение доказывается путем нахождения предела среднего степенного при k → 0. Для того чтобы сделать такой предельный переход, обе части формулы среднего степенного возводятся в степень k, затем x¯k и все xki представляются разложением в степенные ряды:
1 + |
k ln x¯ |
|
(k ln x¯)2 |
|
k ln xi |
|
(k ln xi)2 |
||
|
+ |
|
+ · · · = |
αi(1 + |
|
+ |
|
+ · · ·), |
|
1! |
2! |
1! |
2! |
||||||
далее в обеих частях полученного выражения сокращаются единицы (1 = αi) , и эти обе части делятся на k. Теперь при k = 0 получается следующее равенство:
ln x¯ = αi ln xi,
откуда x¯ = xαi i , что и требовалось доказать.
Средние геометрические используются при построении некоторых специальных индексов. Но это тема следующей главы. Простые примеры использования средней геометрической дает производственная функция.
Пусть в производственной функции Кобба—Дугласа так называемая отдача на масштаб постоянна, т.е. сумма показателей степеней в выражении функции равна единице, и при увеличении использования ресурсов в одинаковое количество раз выпуск продукции растет в такое же количество раз:
X = aCαL1−α,

58 |
Глава 2. Описательная статистика |
или в более развернутой форме:
X = (CaC )α(LaL)1−α,
где aC — коэффициент фондоотдачи при нормальном соотношении между основным капиталом и трудом, aL — коэффициент производительности труда при тех же нормальных условиях.
Нормальное соотношение труда и капитала определяется сложившимся организа- ционно-технологическим уровнем производства. Это — фиксированная величина:
sn = CL .
Откуда aC = a (sn)α−1 , aL = a (sn)α .
Таким образом, в общем случае (при любых соотношениях ресурсов) выпуск продукции является средневзвешенной геометрической потенциального выпуска, который мог бы быть обеспечен основным капиталом при нормальном соотношении его с трудом (величины CaC ), и потенциального выпуска, который обеспечивается трудом при нормальном его соотношении с капиталом (LaL ). Коэффициент a в исходной записи производственной функции равен aαC a1L−α , и он может называться коэффициентом общей производительности ресурсов, поскольку является также среднегеометрической нормальной фондоотдачи и нормальной производительности труда.
Более общая форма связи между выпуском и ресурсами дается производственной функцией с постоянной эластичностью замены ресурсов. В развернутом виде она записывается следующим образом:
−ρ |
+ (1 − α) (LaL) |
−ρ |
−ρ1 |
X = α (CaC ) |
|
. |
Это — пример использования среднего степенного при нецелочисленных значениях параметра степени, поскольку ρ (равный −k в общей формуле среднего степенного) может принимать любые значения на отрезке [−1, +∞] (при ρ → 0, в силу приведенного выше доказательства, производственная функция с постоянной эластичностью замены преобразуется к форме Кобба—Дугласа). От величины этого параметра зависят возможности взаимного замещения ресурсов, допускаемые в данной модели производства. Чем выше его величина, тем более затруднено это замещение.
Такое свойство производственной функции с постоянной эластичностью замены эквивалентно известному свойству среднего степенного: оно увеличивается с ростом k.
Среднее степенное увеличивается с ростом k, в частности, по возрастанию средние степенные располагаются в следующем порядке: гармоническое, геометрическое, арифметическое, квадратическое. Это свойство иногда называют мажорантностью средних.

2.2. Средние величины |
|
|
|
|
|
|
|
|
59 |
||
Пусть x¯(k) — среднее степенное, пусть далее k2 |
> k1 , и требуется доказать, |
||||||||||
что x¯(k1) > x¯(k2). |
|
|
|
|
|
|
|
|
|
|
|
Эти средние можно записать в следующем виде: |
|
|
|
|
|
||||||
|
|
|
k1 |
|
1 |
|
|
k1 |
|
1 |
|
|
|
|
|
k1 |
|
|
k1 |
||||
x¯ (k1) = |
αi |
xk2 |
k2 |
|
|
, x¯ (k2) = |
αixk2 |
k2 |
, |
||
|
|
|
|
||||||||
|
|
i |
|
|
|
|
i |
|
|
|
|
и ввести промежуточные обозначения (чтобы не загромождать изложение):
yi = xki 2 ,
q = k1 , k2
f (y) = yq ,
v= d2f = q (q − 1) yq−2, dy2
a1 = αif (yi), a2 = f |
αiyi . |
В этих обозначениях утверждение, которое следует доказать, записывается следующим образом:
|
1 |
|
1 |
|
a k1 |
> a k1 . |
|||
2 |
1 |
|
||
Далее рассматривается три возможных случая:
1)k2 > k1 > 0,
2)k2 > 0 > k1,
3)0 > k2 > k1.
Впервом случае q < 1, v < 0 , т.е. функция f вогнута (выпукла вверх) и a2 > a1 по определению такой функции. После возведения обеих частей этого неравенства
вположительную степень 1 k1 знак его сохраняется, что и завершает доказательство в этом случае.
Во втором и третьем случаях v > 0, и функция f выпукла (выпукла вниз). Поэтому a2 < a1 , и после возведения обеих частей этого неравенства в отрицательную степень 1 k1 оно меняет знак, приобретая тот, который нужно для завершения доказательства.
Свойство мажорантности средних выражается и в том, что предельные значения среднего степенного при k = ±∞ равны, соответственно, максимальному и минимальному значению признака в выборке.
60 |
Глава 2. Описательная статистика |
Для доказательства этого факта в выражении среднего выносится за скобки x1 :
N |
|
1 |
|
xi |
k k |
||
x¯ = x1 α1 + αi |
. |
||
x1 |
|||
i=2 |
|
||
|
|
Если xi упорядочены по возрастанию и x1 = min xi , то xi x1 1, и при k → −∞
k
выражение в скобках стремится к αi , где k — число объектов, для которых
i=1
усредняемый признак минимален (если минимум единственный, то k = 1), т.е. конечно. Это выражение возводится в степень 1 k , которая стремится к нулю при k → −∞. Следовательно, среднее степенное при k → −∞ равно минимальному значению усредняемых признаков.
Предположив теперь, что xi упорядочены по убыванию, аналогичным образом можно доказать, что среднее степенное при k → +∞ равно максимальному значению признака по совокупности.
Существует наиболее общая запись средневзвешенного:
x¯ = f −1 αif (xi) . (2.4)
Если f — степенная функция xk , то речь идет о средней степенной, если f — логарифмическая функция ln x, то это — средняя логарифмическая, которая является частным случаем средней степенной при k = 0, если f — показательная функция ax , то это — средняя показательная и т.д.
Особенностью средних относительных величин является то, что они, как правило, рассчитываются как средние взвешенные.
Пусть i-й объект, i = 1, . . . , N характеризуется зависимыми друг от друга объемными величинами yi и xi. Показателем этой зависимости является относительная величина ai = yi xi . Это может быть производительность, фондовооруженность труда, рентабельность и т.д. Понятно, что средняя по совокупности объектов относительная величина a (знак черты над символом, обозначающим среднее относительное, часто опускается) рассчитывается по следующей формуле:
a = |
yi |
, |
|
||
|
xi |
|
которая легко преобразуется в формулу средней взвешенной:
a = |
αxai, где αx |
= |
|
xi |
, или |
||||||||
|
|
|
|||||||||||
|
|
|
i |
|
i |
|
|
|
|
xi |
|||
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
y |
= |
|
yi |
|
|
|
||||
a = |
|
|
|
|
, где α |
|
|
|
|
|
. |
|
|
|
|
y |
i |
|
|
|
|
|
|||||
|
|
αi |
|
|
|
|
|
yi |
|||||
|
|
|
|
|
|
|
|||||||
ai
2.2. Средние величины |
61 |
Таким образом, если веса рассчитываются по структуре объемных величин, стоящих в знаменателе, то средняя относительная является средней взвешенной арифметической, если эти веса рассчитываются по объемным величинам, стоящим в числителе, то она является средней взвешенной гармонической.
Формально можно рассчитать простую среднюю (например, арифметическую)
a = |
1 |
ai, |
|
N |
|||
|
|
но содержательного смысла она иметь не будет. Это становится понятным, как только осуществляется попытка привести слагаемые yi xi к общему знаменателю. Тем не менее, такая средняя также может использоваться в анализе. Например, ее иногда полезно сравнить с фактической средней a для выявления некоторых характеристик асимметрии распределения признака по совокупности. Если a > a , то в совокупности преобладают объекты с повышенной величиной ai , и, повидимому, имеет место правая асимметрия, в противном случае в совокупности больший удельный вес занимают объекты с пониженной ai (левая асимметрия). Однако в статистике имеются более четкие критерии асимметрии распределения.
Особое место среди средних относительных занимают средние темпы роста. Темпы роста величин типа потока выражают отношение потока за единицу (период) времени к потоку за некоторую предыдущую единицу (предыдущий период) времени. Темпы роста величин типа запаса показывают отношение запаса в момент времени к запасу в некоторый предыдущий момент времени. Такой же смысл имеют и средние темпы роста. Средние за период темпы роста рассчитываются обычно как средние геометрические.
Пусть x0, x1, . . . , xN значения некоторой объемной величины в моменты времени t0, t1, . . . , tN , если эта величина типа запаса, или в последнюю единицу времени, соответственно, 0-го, 1-го и т.д., N -го периода времени, если речь идет о величине типа потока (t0 — последняя единица времени 0-го периода, [ti−1 + 1, ti] — i-й период). Как и прежде, τi = ti −ti−1, i = 1, . . . , N , τ = τi. Предполагается, что i — целые положительные числа.
Тогда |
|
|
|
|
|
λi = |
xi |
|
— темп роста за i-й период времени, |
||
|
|
|
|||
|
xi−1 |
||||
|
xN |
|
|
N |
|
λ = |
|
= λi — общий темп роста. |
|||
x0 |
|||||
|
|
i=1 |
|||
|
|
|
|
||
Если все периоды одинаковы и равны единице (τi |
= 1), то средний в единицу |
||||||||
времени темп роста определяется по формуле: |
|
|
|
|
|||||
|
xN |
|
1 |
|
|
1 |
|
|
|
¯ |
|
N |
|
|
|||||
|
|
N |
|
||||||
λ = |
|
= |
λi |
, |
|||||
x0 |
|||||||||
|
|
|
|
|
|
|
|
||

62 |
Глава 2. Описательная статистика |
т.е. он равен простому среднему геометрическому темпу по всем периодам.
В общем случае (при разных τi) данная формула приобретает вид средневзвешенной геометрической:
|
|
|
|
|
xN |
|
1 |
|
|
|
|
|
¯ |
|
τ |
¯αi |
|
||
|
|
|
λ = |
x0 |
= |
λi |
, |
||
|
|
|
|
|
|
|
|
||
где |
¯ |
1/τi |
— средний за |
единицу |
времени |
темп роста в i-м периоде, |
|||
λi |
= λi |
||||||||
αi = τ i |
τ . |
|
|
|
|
|
|
|
|
Для величин типа запаса имеется еще одна форма средних темпов роста: отношение средней хронологической за период времени к средней хронологической за некоторый предыдущий период. Такую форму средних можно рассмотреть на следующем примере.
Пусть x0, x1, x2 — значение величины типа запаса в три момента времени: на начало первого периода, конец первого периода, который одновременно является началом второго периода, конец второго периода. Оба периода времени одинаковы. Средние хронологические за первый и второй периоды времени равны, соответственно,
x¯1 = (1 − α) x0 + αx1, x¯2 = (1 − α) x1 + αx2.
Темп роста средней величины типа запаса |
¯ |
x¯2 |
x¯1 |
можно выразить через |
λ = |
|
средние взвешенные темпов роста за каждый из двух периодов времени λ1 = x1 x0 ,
λ2 = x2 x1 |
следующим образом: |
|
|
|
|
|
|
|
|
|
|
||
λ¯ = α11λ1 + α21λ2, где α11 = |
(1 − α) x0 |
, α21 = |
αx1 |
, α12 + α21 = 1, или |
|||||||||
|
x¯1 |
|
|
||||||||||
|
|
|
|
|
|
|
x¯1 |
|
|
|
|||
λ¯ = |
|
1 |
, где α2 |
= |
(1 − α) x1 |
, α2 |
= |
αx2 |
, α2 |
+ α2 |
= 1. |
||
α2 |
/λ1 + α2/λ2 |
|
x¯2 |
||||||||||
|
1 |
|
x¯2 |
2 |
|
1 |
2 |
|
|||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, темп роста средней хронологической является средней взвешенной арифметической темпов роста за отдельные периоды, если веса рассчитываются по информации первого периода, или средней взвешенной гармонической, если веса рассчитываются по информации второго периода.
Если коэффициент α, представляющий внутрипериодную динамику, различается по периодам, т.е. динамика величины в разных периодах качественно различна, то темп роста средней хронологической перестает быть средней арифметической или гармонической темпов роста по периодам, т.к. сумма весов при этих темпах роста не будет в общем случае равняться единице.
В разных ситуациях средние темпы роста могут рассчитываться различным образом, что можно проиллюстрировать на простых примерах, взятых из финансовых расчетов.
