Вопрос 25. Поляризация волн. Основные параметры. Виды поляризации.

Для описания ориентации волн в пространстве вводят понятие поляризации. Под плоскостью поляризации подразумевают плоскость, проходящую через направление распространения волны и параллельно вектору .

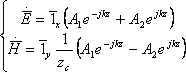
          Для того чтобы проанализировать возможные случаи поляризации рассмотрим следующие решения. Пусть плоская волна представляет собой композицию решений из (1) и (2), которые также являются решением уравнения Гельмгольца.

1. Пусть слагаемые в соотношении (3) синфазные, т.е. ;;.

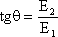Тогда результирующий вектор , а стало быть, и плоскость поляризации оказываются повернутыми на угол Q относительно оси x, причем положение плоскости поляризации в процессе распространения волны остается неизменным.

2. Пусть слагаемые равны по амплитуде, а по фазе отличаются на 90°:

, , тогда получим:

Определим положение угла Q: 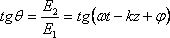      . В этом случае положение плоскости поляризации изменяется во времени и пространстве. Если зафиксируем некоторую плоскость, то векторбудет вращаться со скоростьюV, и его конец будет описывать окружность. Если зафиксируем время, то вектор будет описывать спираль вдоль оси z. Этот случай поляризации называется круговой, т.е. в процессе распространения плоскость поляризации вращается. Это был случай левой поляризации. Для получения правой поляризации надо, чтобы

, .

   Условием круговой поляризации волны является временная и пространственная квадратура составляющих. Компоненты должны быть взаимно ортогональны и должны отличаться по фазе на 90° и должно выполняться условие равенства амплитуд. В том случае, когда одно из условий не выполняется, имеем эллиптическую поляризацию. В любой фиксированной плоскости вектор Е движется по эллиптической замкнутой кривой. Степень поляризации характеризуют отношением большой оси к малой.

Вопрос 26. Волновые явления на границе раздела двух сред.

Плоские волны произвольной ориентации.

 В предыдущих параграфах мы рассматривали плоские волны, распространяющиеся вдоль осей декартовой системы. Признаком распространения является .

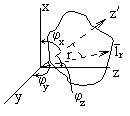Предполагаем, что среда без потерь.где,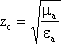

Косинусы углов, определяющих направление волны, называются направляющими. Уравнение фазовой плоскости (=const):

Где 

Тогда скалярное произведение:

 Мы предполагали, что среда без потерь. В случае среды с потерями соотношения не меняются, только вместо k подставляется  = — j. Перед началом рассмотрения волновых явлений дадим ряд определений.

 Плоскость, проходящая через нормаль к границе раздела и параллельно направлению распространению волны, называется плоскостью падения. Вектор перпендикулярен направлению распространения волны, а относительно плоскости падения волны он ориентирован произвольным образом.

  Не теряя обобщенности рассуждений, достаточно рассмотреть два случая ориентации .

1.) перпендикулярен плоскости падения (нормальная поляризация)

2.) параллелен плоскости падения (параллельная поляризация)

  При произвольной ориентации вектора , он может быть представлен как суперпозиция двух этих случаев.