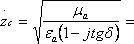- •Вопрос 2. Первое уравнение Максвелла в интегральной и дифференциальной формах.
- •Вопрос 3. Второе уравнение Максвелла в интегральной и дифференциальной формах.
- •Вопрос 4. Третье уравнение Максвелла в интегральной и дифференциальной формах.
- •Вопрос 5. Четвёртое уравнение Максвелла в интегральной и дифференциальной формах.
- •Вопрос 6. Уравнение непрерывности
- •Вопрос 7. Закон Ома в Дифференциальной форме.
- •Вопрос 8. Материальные уравнения.
- •Вопрос 9. Уравнения Максвелла для различных сред.
- •Вопрос 10. Учёт сторонних источников в Уравнениях Максвелла.
- •Вопрос 11. Полная система граничных условий
- •Вопрос 12. Баланс Энергии эмп. Теорема Умова-Пойнтинга в интег-ой и диф-ой формах.
- •Вопрос 13. Плотность энергии эмп.
- •Вопрос 14. Скорость распространения Электромагнитной энергии.
- •Вопрос 15. Уравнения Максвелла для монохром-ого поля. Метод комплексных амплитуд.
- •Вопрос 16. Система уравнений монохроматического поля.
- •Вопрос 17. Баланс средней за период мощности. Комплексная мощность.
- •Вопрос 18. Теорема единственности для внутренних и внешних задач электродинамики.
- •Вопрос 19. Однородные и неоднородные волновые уравнения для векторов эмп.
- •Вопрос 20. Векторный и скалярный потенциал. Вектор Герца.
- •Вопрос 21. Электродинамические потенциалы электромагнитного поля.
- •Вопрос 22. Плоские эмп в однородной изотропной среде без потерь.
- •Вопрос 23. Плоские эмп в однородной изотропной среде с проводимостью, отличной от 0.
- •Вопрос 24. Волны в диэлектриках и проводниках.
- •Вопрос 25. Поляризация волн. Основные параметры. Виды поляризации.
- •Вопрос 26. Волновые явления на границе раздела двух сред.
- •Вопрос 27. Падение плоской волны на границу раздела двух диэлектриков. Угол Брюстера.
- •Вопрос 28. Полное отражение от границы раздела двух диэлектриков.
- •Вопрос 29. Падение плоской волны на границу поглощающей среды.
- •Вопрос 30. Приближенные граничные условия Леонтовича-Щукина.
- •Вопрос 31. Поверхностный эффект. Эквивалентный поверхностный ток. Поверхностное сопротивление.
- •Эквивалентный поверхностный ток
- •7.8.4. Поверхностное сопротивление проводника
- •Вопрос 32. Теорема эквивалентности.
- •Вопрос 33. Лемма Лоренца
- •Вопрос 34. Теорема взаимности
- •Вопрос 35. Излучение электромагнитных волн. Элементарный электрический вибратор.
- •Вопрос 36. Поле элементарного электрического вибратора в дальней, ближней и промежуточных зонах.
- •Вопрос 37. Диаграмма направленности и мощность излучения элементарного электрического вибратора.
- •Вопрос 38. Элементарный магнитный вибратор.
- •Вопрос 39. Эквивалентные источники эмп. Принцип Гюйгенса-Кирхгофа.
- •Вопрос 40. Элементарный излучатель Гюйгенса.
- •Вопрос 41. Дифракция эмв. Методы решения задач дифракции
- •Вопрос 42. Метод Фурье решения задач дифракции.
- •Вопрос 43. Приближенные методы решения задач дифракции. Приближение Гюйгенса-Кирхгофа. Метод геометрической оптики. Геометрическая теория дифракции.
Вопрос 21. Электродинамические потенциалы электромагнитного поля.
Рассмотрим систему уравнений Максвелла для монохроматического поля, записанную для комплексных амплитуд векторов Е и Н:
![]()
Используя равенство div(μHm) = O, являющееся следствием второго уравнения системы (2.51), представим вектор Нm в виде
![]()
![]()
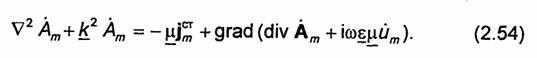
![]()
которое обычно называют условием калибровки Лоренца. При этом равенство (2.54) переходит в неоднородное векторное уравнение Гельмгольца
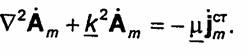
Отметим, что условие калибровки (2.55) позволяет выразить через один векторный потенциал не только вектор Нm, но и вектор
Ёm. Действительно, выражая йт из (2.55) и подставляя в (2.53), получаем
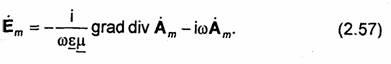
Предположим
вначале, что среда, в которой ищется
поле, является идеальным диэлектриком
![]() В
этом случае выражение дляАт
может
быть получено из формулы (2.50) заменой
функции
В
этом случае выражение дляАт
может
быть получено из формулы (2.50) заменой
функции
![]()
![]() -комплексная
амплитуда плотности сторонних
электрических токов. Так как
-комплексная
амплитуда плотности сторонних
электрических токов. Так как![]() ,
,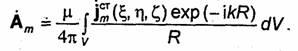
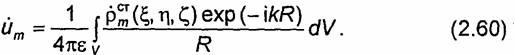
Вопрос 22. Плоские эмп в однородной изотропной среде без потерь.
Будем
рассматривать свободные (существующие
без сторонних источников) гармонические
колебания электромагнитного поля в
однородной изотропной среде без
потерь(![]() ).
В этом случае для определения характеристик
электромагнитного поля удобно
воспользоваться однородными уравнениями
Гельмгольца относительно векторов
электромагнитного поля.
).
В этом случае для определения характеристик
электромагнитного поля удобно
воспользоваться однородными уравнениями
Гельмгольца относительно векторов
электромагнитного поля.
![]()
![]()
![]() -волновое
число.
-волновое
число.
Будем полагать, что волна, распространяется вдоль оси Z, т.е. вектор Пойнтинга:
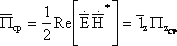
Решение
каждого из уравнений:
![]() (9)
(9)
![]()
так как, по определению, поле должно быть неизменно в плоскости распространения волны, то:
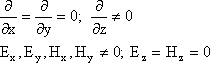 Получим
систему решений:
Получим
систему решений:![]()
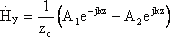
![]() (18)
(18)
 (19),
(19),
где
 ,
[Ом] — характеристическое сопротивление
среды, определяющееся свойствами среды.
,
[Ом] — характеристическое сопротивление
среды, определяющееся свойствами среды.
Вопрос 23. Плоские эмп в однородной изотропной среде с проводимостью, отличной от 0.
В среде с проводимостью отличной от нуля энергия электромагнитной волны частично расходуется на возбуждение и поддержание токов проводимости, т.е. волна в процессе распространения затухает. В общем случае наряду с джоулевыми потерями в среде могут присутствовать также диэлектрические и магнитные потери. В этом случае:
![]()
![]()
![]()
В
этом случае решения по форме совпадают
с решениями, полученными в предыдущем
параграфе. 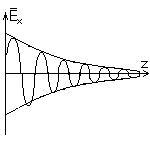
![]()
![]() Перейдем
для уяснения физического смысла к
мгновенным значениям:
Перейдем
для уяснения физического смысла к
мгновенным значениям:
![]()
Степень
убывания амплитуды:
![]() -характеризует
ослабление волны.
-характеризует
ослабление волны.
Будем
рассматривать случай, когда потери в
среде вызваны конечной проводимостью
(только Джоулевы потери):
![]() и
и![]() ,
,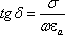
![]()
Таким образом поле плоской волны, распространяющейся в среде с потерями, может быть представлено следующими соотношениями:
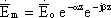
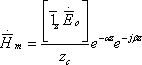
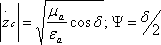
Вопрос 24. Волны в диэлектриках и проводниках.
Для
реальных диэлектриков .
![]() Используя неравенство, скобку можно
представить в виде ряда Маклорена:
Используя неравенство, скобку можно
представить в виде ряда Маклорена:
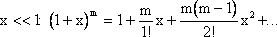
![]()
Ограничиваясь тремя элементами разложения, пренебрегая всеми остальными, получаем:
![]() Приравнивая
реальную и мнимую части, получим:
Приравнивая
реальную и мнимую части, получим:
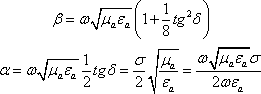
Используя выражение для b, получим:
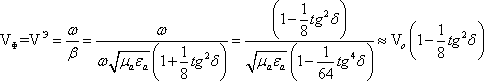
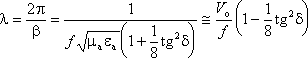
Vо — скорость света в среде.
Из результатов следует, что параметры плоской волны в реальных диэлектриках мало отличаются от параметров в среде без потерь. Постоянная затухания в реальных диэлектриках является очень малой величиной и в первом приближении не зависит от частоты. В реальных диэлектриках дисперсионные свойства проявляются слабо.
В
проводящих средах
![]() .
Общее выражение:
.
Общее выражение:
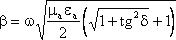
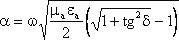
Пренебрегая
единицей, получим (![]() линейноым образо зависят от частоты):
линейноым образо зависят от частоты):
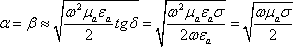 b
и a не линейно зависят от w, следовательно,
с изменением w они будут существенно
изменяться. Получим выражение для
фазовой скорости:
b
и a не линейно зависят от w, следовательно,
с изменением w они будут существенно
изменяться. Получим выражение для
фазовой скорости:
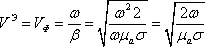 и
для длины волны:
и
для длины волны:
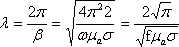
Характеристическое
сопротивление: