Вопрос 16. Система уравнений монохроматического поля.

  Известно, что уравнения Максвелла относятся к линейным дифференциальным уравнениям. Поэтому в случае гармонических электромагнитных полей в уравнениях Максвелла можно перейти к комплексным амплитудам.

.

т.к. ,

  Переходя во втором уравнении Максвелла к комплексным амплитудам получим: (10).

, где (11)

В случае гармонических полей при использовании метода комплексных амплитуд 3 и 4 уравнения Максвелла являются следствием первых двух. Окончательно получим: 

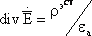       Итак, когда имеются сторонние источники:

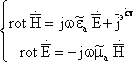
Уравнения Максвелла без учета сторонних источников:

Подставляя вторую систему в первую, с использованием метода комплексных амплитуд, получим:

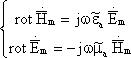
Вопрос 17. Баланс средней за период мощности. Комплексная мощность.

Теорема Умова-Пойнтинга и соответствующее ей аналитическое соотношение

Получим уравнение баланса для средней за период значения мощности гармонического электромагнитного процесса. Необходимо для каждого из слагаемых уравнения получить величину, определяемую соотношением. Т. к. в соотношении осуществляется интегрирование по времени, а анализируется гармонический электромагнитных процесс, то, естественно, надо воспользоваться методом комплексных амплитуд. Непосредственная замена мгновенных функций, соответствующими комплексными аналогами возможна только в линейных уравнениях. В данном случае непосредственная замена мгновенных векторов электромагнитного поля невозможна.

Для начала получим среднее за период значение вектора Пойнтинга:

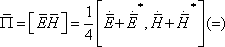
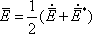
Среднее за период значение потока мощности:

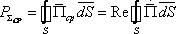
Таким образом, в результате проделанных нами вычислений, получили:

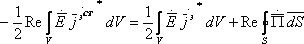
          В среднем за период, мощность сторонних источников расходуется на потери внутри объема и частично уходит во внешнее пространство, через поверхность S.

Средняя за период энергия электрического поля:

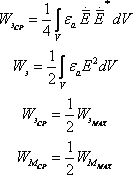
Вопрос 18. Теорема единственности для внутренних и внешних задач электродинамики.

Внутренние задачи электродинамики имеют единственное решение, если выполняется одно из следующих условий:

          1.Если в каждой точке М поверхности S задана проекция вектора на плоскость, касательную к поверхности S в точке М:— "Е" задача.

          2. Если в каждой точке M поверхности S задана проекция вектора на плоскость, касательную к поверхности S в точке М:— "Н" задача.

          3. Если на части поверхности S в каждой точке задана проекция вектора на плоскость, касательную к S в этой точке, а на другой части плоскости задана проекция векторакасательная к S в точке М:

—"ЕН" задача.

          4. Если в каждой точке поверхности S задано соотношение между проекциями векторов ина плоскость, касательную к S в точке М.

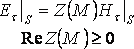
   Для обеспечения единственности решения внешних задач электродинамики необходимо выполнение одного из условий 1-4, плюс к этому должно выполнятся одно из условий, описывающее поведение электромагнитного поля при бесконечно удаленных точках (при r®Ґ).

          1. Принцип предельного поглощения () требует, чтобы эта зависимость была, т.е. каждая из составляющих поля должна убывать с увеличением расстояния быстрее, чем. В реальных средах имеются пусть очень малые, но конечные по величине потери, т.е.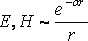. Поэтому, в бесконечно удаленных точках, электромагнитное поле равно нулю.

          2. Если в среде отсутствуют потери и принцип предельного поглощения не применим, в этом случае векторы электромагнитного поля должны удовлетворять следующим соотношениям:

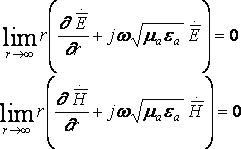—условия Зоммерфельда.