Вопрос 38. Элементарный магнитный вибратор.

Представим вначале магнитный излучатель в виде фиктивного проводника длиной l^м с протекающим по нему фиктивным переменным током I_ст^м .

Применяя принцип перестановочной двойственности (3.23), запишем поле магнитного излучателя в ближней и дальней зоне:

Ближняя зона: Дальняя зона:

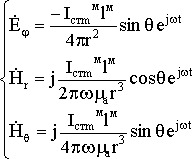
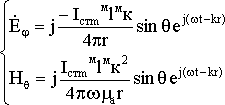
Можно отметить, что свойства магнитного излучателя полностью совпадают со свойствами электрического излучателя, как в ближней, так и в дальней зонах.

Диаграмма направленности магнитного излучателя аналогична диаграмме направленности электрического излучателя: ,

и представляет собой тор в сферической системе координат.

Мощность излучения магнитного излучателя находим, используя принцип перестановочной двойственности: ,

где R_изл^м – сопротивление излучения магнитного излучателя:

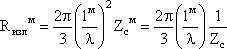, (3.25)

Здесь Z_С ^м = (посколькуZ_С = ).

В заключение рассмотрим переход от фиктивного магнитного излучателя к его физически осуществимой модели (т.е. реальной конструкции).

Рассмотрим силовые линии электрического и магнитного поля, создаваемые элементарным электрическим излучателем. Пользуясь принципом перестановочной двойственности, следует предположить, что некая конструкция, имеющая тот же характер структуры поля, отличающуюся только заменой наи будет являться элементарным магнитным излучателем. Такая конструкция вам известна из курса общей физики – это рамка с током.

Следовательно, рамка с током является физической реализацией магнитного излучателя. Такой магнитный излучатель можно считать элементарным, если длина контура L   .

Вопрос 39. Эквивалентные источники эмп. Принцип Гюйгенса-Кирхгофа.

При анализе конкретных излучающих систем часто возникают ситуации, когда распределение токов в системе либо неизвестно, либо имеет крайне сложный характер, но зато можно считать известным поле на некоторой замкнутой поверхности, охваты­вающей излучающую систему. В этих случаях поле, излучаемое системой, можно найти непосредственно по значениям векторов Ё и Н на этой поверхности.

Задача формулируется следующим образом. Пусть источники сосредоточены в ограниченной области V. Характер источников и их расположение неизвестны, но зато известны значения векторов Ё и Н на внешней по отношению к источникам стороне пове­рхности S, ограничивающей объем V.

Предположим, что на S отсутствуют поверхностные токи и заряды. Тогда на S должны выполняться следующие условия:

 

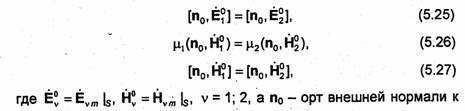
поверхности S.

плотность эквивалентных поверхностных зарядов

 Магнитный векторный потенциал вы­числяется по аналогичной формуле, вытекающей из (2.61) и перестановочной двойственности уравнений Максвелла:

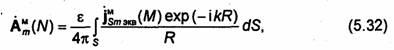
Принцип эквивалентности тесно связан с известным принципом Гюйгенса-Кирхгофа. В соответствии с этим принципом, каждая точка фазового фронта распространяющейся волны может рассматриваться как точечный источник сформированной волны. Аналитически принцип Гюйгенса сформулирован Кирхгофом, поэтому его так назвали.

Принцип Гюйгенса-Кирхгофа применим и к поверхностям, которые не совпадают с фазовым фронтом волны. В этом случае, определяя возбуждение точечных источников нужно учитывать фазовый сдвиг каждого из них. Принцип Гюйгенса-Кирхгофа широко применяется в теории антенн при вычислении поля излучаемого апертурными антеннами.