книжка умняшкина по моцос

Следствие. Обратная матрица W-1=W, и формула обратного ДПУ совпадает с формулой прямого ДПУ (3.19), т.е. Y=WX, X=WY,

1 2n −1

xk = ∑y j wk ( j / 2n ) .

2n j=0

Пример 5. Построим матрицу ДПУ для 4-точечного преобразования,

3.8. Дискретное преобразование Хаара

Определение. Дискретным преобразованием Хаара (ДПХ) вектора X = (x0 , x1,K, x2n −1 ) назовем вектор Y = (y0 , y1,K, y2n −1 ), компоненты которого находятся по формуле:

где hk(t) – k-я функция системы Хаара (см. раздел 1.7).

Замечание. Положив, что xj – это отсчёты некоторой функции, xj=f(j/2n), определённой на отрезке t [0;1], формулу (20) также можно рассматривать как приближённое вычисление по формуле прямоугольников интеграла:

(с точностью до множителя 1 2n ), где ck представляет собой k-й коэффициент Фурье разложения функции f(t) по системе Хаара.

71

Y=HX – ортогональна, т.е. HT = H−1 .

◄ Обозначим U=HHT и покажем, что матрица U – единичная. Рассмотрим элемент k-ой строки j-ого столбца матрицы U, который представляет собой скалярное произведение k-ой строки матрицы H и j-ого столбца

во 1° системы Хаара, пример 1.12), то выражение для uk,j можем переписать:

в силу ортонормированности системы Хаара (см. теорему 1.13). ►

Пример 6. Построим матрицу ДПХ для 4-точечного преобразования,

N=22.

◄ Построив по определению (см. пример 1.12) первые функции h0(t), h1(t), h2(t), h3(t), находим значения hj(j/4), k,j=0,1,2,3, и получаем сле-

ДПХ и ДПУ также обладают быстрыми алгоритмами вычислений. Данные преобразования вычисляются намного быстрее ДПФ, так как реализуются только за счёт операций сложения и вычитания чисел, не требуя операций умножения или деления (за исключением окончательной нормировки коэффициентов, ~N умножений, которая на практике требуется не всегда).

72

3.9. Некоторые применения дискретных ортогональных преобразований

Положим, что N=2n. Используя свойство ДПФ свёртки (см. свойство 5° ДПФ), можно вычислить вектор-свёртку следующим образом.

двух БПФ размерности 2N=2n+1 потребует (см. раздел 3.6) примерно

73

ны интервалов, dj=xmin+(j+0,5)q. Правило квантования имеет простой вид: если X ∆j, то Q(X)=dj. Очевидно, что ошибка квантования при этом:

средними значениями. В частности, для характеристики ошибки квантования используется величина

где обозначение М используется для математического ожидания, а горизонтальная черта означает операцию усреднения. При достаточно малой

= − ˆ

величине дискрета квантования q ошибку квантования E X X можно считать случайной величиной, подчиняющейся равномерному закону распределения на отрезке [− q 2; q 2]. Тогда (21) представляет собой

дисперсию ошибки квантования. Как было установлено в курсе теории вероятностей, для равномерного закона распределения случайной величины E ~ R[− q 2; q 2] математическое ожидание М(E)=0, а дисперсия

ошибки квантования ε2 = D(E) = q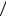2 12 .

Оптимальное квантование Ллойда-Макса

Вновь положим, что случайная величина непрерывного типа X принимает значения из какого-то диапазона [xmin;xmax), причем известна её функция плотности распределения вероятностей fX(x), fX(x)>0 при

X [xmin;xmax) и fX(x)=0 при X [xmin;xmax). Разобьём интервал [xmin;xmax) на N, вообще говоря, неравных частей: ∆j=[tj;tj+1), j=0,…,N-1, t0=xmin, tN=xmax. Внутри каждого подынтервала ∆j расположим точку dj – уровень кванто-

вания. Правило квантования имеет тот же вид, что и ранее: если X ∆j, то Q(X)=dj. Однако теперь параметры квантования – пороги {t j }Nj =−11 и уров-

ни {d j }Nj=−01 – будем искать с точки зрения минимизации величины (21)

как функции данных параметров:

ε 2 = g(t1 ,K,tN −1;d0 ,K, d N −1 ) = M[(X −Q( X ))2 ]=

Необходимым условием минимума функции (22) является равенство нулю частных производных.

76

Заметим, что выражение (24) представляет собой среднее значение случайной величины X при условии, что последняя попала в интервал ∆j. То есть (24) – это условное математическое ожидание: d j = M( X | X ∆ j ) .

Решение системы уравнений (23), (24) определяет квантователь Ллойда-Макса и, как можно было бы показать, дает минимальное значение ошибки (22). В общем случае решение системы уравнений (23), (24) необходимо искать численными методами. Отметим также, что все приведённые рассуждения, которые привели к построению данной системы уравнений, сохраняются в силе и для общего случая, когда функция плотности распределения принимает ненулевые значения на всей числовой оси, т.е. когда t0= xmin=-∞, tN=xmax=+∞.

77

Пример 9. Найти параметры оптимального квантователя Ллойда-Макса для квантования с N уровнями для случайной величины, имеющей равномерное распределение на интервале [a,b], т.е. X~R[a,b].

◄ Функция плотности распределения имеет в данном случае вид:

Тогда для уравнений (24) получаем:

С учётом (23) и условий t0=a, tN=b, для параметров оптимального квантователя Макса получаем окончательно следующую систему уравнений, которая в данном случае принимает линейный вид и легко разрешима:

Решение системы – очевидное, определяет рассмотренный выше равномерный квантователь, который для равномерно распределённой случайной величины является также оптимальным в смысле минимизации ошибки (21). ►

Итак, процесс квантования отсчётов дискретного сигнала можно рассматривать как преобразование случайной величины непрерывного

ˆ =

типа X в случайную величину дискретного типа X Q( X ) . Трактуя уровни квантования {d j }Nj=−01 как символы некоторого алфавита, цифро-

вой сигнал можно считать словом, составленным из этого алфавита, буквы которого представляют собой проквантованные отсчёты дискретного сигнала. Такое слово, или «дискретное сообщение», можно представить в двоичном виде. Вопросы эффективного двоичного кодирования дискретных сообщений мы рассмотрим позднее в главе 5.

78