
книжка умняшкина по моцос
.pdf
цательна, расстояние от точки до подмножества (подпространства) всегда существует.
Расстояние ρ(x,L) характеризует наилучшее приближение (т.е. аппроксимацию) элемента x E элементами подмножества L, L E.
Определение. Элемент u L, где L – подмножество из ЛНП E, назы-
вается элементом наилучшего приближения (ЭНП) для произвольно-
го элемента x E, если ρ(x,L)= 
 x − u
x − u
 .
.
ЭНП может также не существовать, или быть не единственным.
Пример 3. Рассмотрим пространство R2, т.е. множество упорядоченных пар вещественных чисел x = (ξ1,ξ2 ) , где ξ1 R, ξ2 R. Введём норму
следующим образом: |
|
|
|
x |
|
|
|
= |
|
ξ1 |
|
+ |
|
ξ2 |
|
(убедитесь самостоятельно, что ак- |
|
|
|
|
|
|
|
|
|||||||||
сиомы нормы выполняются). |
Рассмотрим подмножество L R2, |
|||||||||||||||
L={(ξ1,ξ2) ξ1=ξ2} = {(α,α) α R }. Тогда:
1.L – подпространство в E;
2.Для x=(-1,1) имеем ρ(x,L)=2, причём ЭНП – не единственный.
◄1. Множество L является линейным многообразием (убедитесь самостоятельно). Покажем, что L – замкнуто. Допустим противное: пусть
существует элемент y L, который является предельной точкой множества L. Для элемента y=(β1,β2): β1≠β2. Тогда для любой точки u=(α,α) из множества L расстояние
ρ(y,u)= β1 −α + β2 −α ≥ β1 − β2 =r(y)>0,
т.е. ограничено снизу положительной величиной r=r(y). Следовательно, в окрестности Sr(y) нет ни одного элемента из множества L, и произвольно выбранная точка y L не является предельной для L. Поэтому все предельные точки множества L могут содержаться только в самом этом
множестве, и L является замкнутым линейным многообразием (подпространством) в R2.
|
|
|
|
|
|
|
|
− 2t, |
t < −1 |
|
2. Так как |
f (t) = |
|
t +1 |
|
+ |
|
t −1 |
|
2, |
−1 ≤ t ≤ 1 , |
|
|
|
= |
|||||||
|
|
|
|
|
|
|
|
|
2t, |
1 < t |
|
|
|
|
|
|
|
|
|
||
то для расстояния от точки x=(-1,1) до подпространства L имеем: |
||||||||||||||||
ρ(x,L)= inf |
|
|
|
u − x |
|
|
|
= inf ( |
|
α +1 |
|
+ |
|
α −1 |
|
)=2. |
|
|
|
|
|
|
|
|
|||||||||
u L |
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
11

При этом элементами наилучшего приближения для x являются все точ-
ки отрезка L* = {(α,α) -1≤α≤1}, L* L .►
1.4. Банаховы пространства
Определение. Пусть X – ЛНП. Последовательность {xn} X называ-
ется фундаментальной, если ε>0 N=N(ε): n>N, p N

 xn + p − xn
xn + p − xn 
 < ε . (Здесь N – множество натуральных чисел.)
< ε . (Здесь N – множество натуральных чисел.)
Напоминание. Для случая X=R (множество действительных чисел) в курсе математического анализа был доказан критерий Коши: числовая последовательность {xn} сходится тогда и только тогда, когда она фундаментальна.
Справедлив ли критерий Коши в произвольном ЛНП? Можно показать, что любая сходящаяся последовательность является фундаментальной, а обратное, вообще говоря, не верно.
Определение. ЛНП называется полным, если в нём сходится всякая фундаментальная последовательность. Полное ЛНП называется ба-
наховым.
Пример 4. Простейший пример банахова пространства – множество вещественных чисел R с нормой 
 x
x
 = x .
= x .
Пример 5. Неполное ЛНП – пространство непрерывных на отрезке [0,T]
T
функций с нормой x = ∫ x(t) 2 dt .
0
◄ Любую разрывную, но кусочно-гладкую функцию f(t) можно представить на отрезке длины T в виде ряда Фурье, сходящегося к функции во всех точках непрерывности и к среднему значению функции в точках разрыва:
f (t + 0) |
+ f (t −0) |
|
a |
0 |
∞ |
|
2πkt |
|
2πkt |
|
|
|
= |
|
+ ∑ ak cos |
|
+ bk sin |
|
. |
||
|
2 |
2 |
T |
T |
||||||
|
|
k =1 |
|
|
|
|||||
Очевидно, что частичные суммы ряда Фурье
|
a |
n |
|
2πkt |
|
2πkt |
||
sn (t) = |
0 |
+ ∑ ak cos |
|
+bk sin |
|
|
||
2 |
T |
T |
||||||
|
k =1 |
|
|
|
||||
- непрерывные функции, однако последовательность {sn(t)} не является
12

сходящейся в пространстве непрерывных функций, т.к. сходится к раз-
рывной функции: lim f (t) − sn (t) = 0 . ►
n→∞
Определения. Пусть X – ЛНП (не обязательно банахово), а {xn} – некоторая последовательность, {xn} X. Формально составленная
∞ |
n |
сумма ∑xk |
называется рядом в X, а элемент sn = ∑xk – n-ной час- |
k =1 |
k =1 |
тичной суммой ряда. (Заметим, что n: sn X, см. определение ЛНП).
∞ |
|
|
|
|
|
|
|
Ряд ∑xk называется сходящимся в ЛНП X, |
{xk} X, |
если |
в X |
||||
k =1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
сходится |
последовательность |
элементов |
{sn}, |
sn = ∑xk . |
То |
есть |
|
|
|
|
|
k =1 |
|
|
|
lim sn = s X. Элемент s |
называется |
суммой ряда, |
а |
запись |
|||
n→∞ |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
s = ∑xk |
означает, что ряд сходится в X, и его сумма равна s. |
|
|||||
k =1
1.5. Пространства со скалярным произведением
Обобщим понятие скалярного произведения, известное из курса аналитической геометрии, на произвольные векторные пространства.
Определение. Вещественное линейное пространство E называется евклидовым, если каждой паре его элементов x,y E поставлено в соответствие вещественное число, называемое скалярным произведением (обозначаем <x,y>) так, что выполняются следующие аксиомы.
1°. x E: <x,x>≥0, причем <x,x>=0 x=θ. 2°. x,y E: <x,y>=<y,x>.
3°. x,y E, λ R: <λx,y>=λ<x,y>. 4°. x,y,z E: <x+y,z>=<x,z>+<y,z>.
Заметим, что в данном определении ничего не говорится о нормированности пространства E. Однако всякое евклидово пространство можно превратить в нормированное, если ввести норму элемента следующим образом:
x = < x, x > . |
(3) |
13

Аксиомы нормы 1° и 2° при этом выполняются очевидным образом. Для доказательства выполнения аксиомы 3° (неравенства треугольника) предварительно рассмотрим следующую лемму.
Лемма 1. Норма, введённая в соответствии с (3), удовлетворяет неравенству Коши-Буняковского (или Шварца):
< x, y > ≤ 
 x
x


 y
y
 .
.
◄ Заметим, что λ R:
0 ≤ <x-λy,x-λy> = <x,x>-2λ<x,y>+λ2<y,y>= 
 x
x
 2 − 2λ < x, y > +λ2
2 − 2λ < x, y > +λ2 
 y
y
 2 .
2 .
Поэтому дискриминант полученного квадратичного трехчлена переменной λ: 4(< x, y >)2 −4
 x
x
 2
2 
 y
y
 2 ≤ 0 , что и доказывает неравенство Ко- ши-Буняковского (К-Б). ►
2 ≤ 0 , что и доказывает неравенство Ко- ши-Буняковского (К-Б). ►
Докажем теперь выполнение аксиомы треугольника для нормы (3). Так как

 x + y
x + y
 2 =< x + y, x + y >=
2 =< x + y, x + y >= 
 x
x
 2 + 2 < x, y > +
2 + 2 < x, y > +
 y
y
 2 ≤
2 ≤ 
 x
x
 2 + 2 < x, y > +
2 + 2 < x, y > + 
 y
y
 2 ,
2 ,
то применяя к последнему выражению неравенство К-Б получаем:

 x + y
x + y
 2 ≤
2 ≤ 
 x
x
 2 + 2
2 + 2
 x
x


 y
y
 +
+ 
 y
y
 2 = (
2 = (
 x
x
 +
+ 
 y
y
 )2 ,
)2 ,

 x + y
x + y
 ≤
≤ 
 x
x
 +
+ 
 y
y
 .
.
Определения. Ортогональными элементами евклидова пространст-
ва E называются такие элементы x,y E, что <x,y>=0. Ортогональность элементов обозначаем x y. Очевидно, нулевой элемент ортогонален всем элементам пространства. Ортогональной системой в E называем множество взаимно ортогональных элементов {xn} E.
Теорема 4. Если {xk }kk ==1m – ортогональная система ненулевых элементов
в евклидовом пространстве E, {xk }kk ==1m E, то элементы {xk }kk ==1m – ли-
нейно независимы.
◄ Схема доказательства теоремы аналогична случаю пространств арифметических векторов Rn. ►
Следствие. В n-мерном евклидовом пространстве ортогональная система из n ненулевых элементов образует базис.
В дальнейшем нам понадобятся два свойства скалярного произведения, которые устанавливаются в следующих леммах.
14

Лемма 2. (Свойство непрерывности скалярного произведения.) Пусть в евклидовом пространстве E заданы две сходящиеся последовательно-
сти: {xn} E, lim xn = x E, {yn} E, |
lim yn |
= y E. Тогда числовая по- |
||
n→∞ |
|
n→∞ |
|
|
следовательность |
< xn , yn > |
также |
сходится, |
причём |
lim < xn , yn >=< x, y > . |
|
|
|
|
n→∞ |
|
|
|
|
◄ Имеем: |
|
|
|
|
< xn , yn > − < x, y > = < xn − x, yn > + < x, yn − y > ≤
≤ < xn − x, yn > + < x, yn − y > ≤ 
 xn − x
xn − x


 yn
yn 
 +
+ 
 x
x


 yn − y
yn − y
 . (Последний переход осуществлен на основании леммы 1.) Поскольку
. (Последний переход осуществлен на основании леммы 1.) Поскольку
lim |
|
|
|
xn − x |
|
|
|
= lim |
|
|
|
yn − y |
|
|
|
= 0 и числовая последовательность |
|
|
|
yn |
|
|
|
ог- |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
n→∞ |
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
раничена, выражение в правой части неравенства стремится к нулю при
n→∞. Следовательно, lim < xn , yn >=< x, y > . ►
n→∞
Лемма 3. (Равенство параллелограмма.) Для любых элементов x, y евклидова пространства E и нормы (3) верно:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + y |
|
|
|
|
|
2 + |
|
|
|
x − y |
|
|
|
2 = 2 |
|
|
|
x |
|
|
|
2 +2 |
|
|
|
y |
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
◄ |
|
|
|
x + y |
|
|
|
2 + |
|
|
|
x − y |
|
|
|
2 =< x + y, x + y > + < x − y, x − y >= |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
=< x, x > +2 < x, y > + < y, y > + < x, x > −2 < x, y > + < y, y >= |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= 2 < x, x > +2 < y, y >= 2 |
|
|
|
x |
|
|
|
2 + 2 |
|
|
|
y |
|
|
|
2 . |
► |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Определение. Пространством Гильберта (обычно обозначается H) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
называется евклидово пространство, которое полно в норме (3). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 6. Пространство En арифметических векторов со скалярным |
||||
произведением, |
определенным |
для |
векторов |
x = (x1,K, xn ), |
y = (y1 ,K, yn ) как |
n |
|
|
|
x, y = ∑xk yk |
– полное, т.е. гильбертово. |
|||
k =1
Пример 7. Пространство L2[a,b] кусочно-непрерывных на отрезке t [a,b] вещественных функций с нормой, индуцированной скалярным
произведением < f , g >= ∫ab f (t)g(t)dt - гильбертово. (Заметим, что если требование кусочной непрерывности заменить на непрерывность функ-
15

ций, полученное пространство не будет полным, см. пример 5.) Проверьте (самостоятельно), что так определенное скалярное произведение удовлетворяет аксиомам 1°-4°.
Замечание. Строго говоря, пространство, обозначаемое L2[a,b], определяется на более широком классе функций. Для строгого определения данного пространства требуется введение меры Лебега и интеграла Лебега, что выходит за рамки данного пособия.
Для пространств Гильберта решение задачи аппроксимации, т.е. отыскания элемента наилучшего приближения, принимает наиболее общий вид.
1.6. Аппроксимация в гильбертовом пространстве
Сформулируем задачу, которую будем рассматривать в данном разделе. Пусть H – гильбертово пространство, а L – подпространство в H, L H. Для произвольного элемента x H необходимо найти элемент наилучшего приближения (ЭНП) y L, для которого ρ(x, y) = ρ(x, L) , то
есть: |
|
|||||||||||||||
|
|
|
x − y |
|
|
|
= inf |
|
|
|
x −u |
|
|
|
. |
(4) |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
u L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Теорема 5. Существует единственный ЭНП y L, который является решением задачи аппроксимации (4).
◄ Докажем сначала существование ЭНП. Обозначим |
d = inf |
|
x −u |
|
|
|
. |
||||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
u L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uε L: |
||||||
Из |
определения точной |
нижней грани |
следует, что |
ε>0 |
|||||||||||||
d ≤ |
|
|
|
x − uε |
|
|
|
< d + ε . Тогда |
взяв числовую |
последовательность |
|
εk=1/k, |
|||||
|
|
|
|
|
|||||||||||||
k=1,2,…, сможем построить последовательность элементов {uk} L такую, что
d ≤ 
 x − uk
x − uk 
 < d + k1 .
< d + k1 .
Покажем, что {uk} – фундаментальная последовательность. С использованием равенства параллелограмма (лемма 3) имеем:
|
|
|
|
x − un |
|
|
|
2 + 2 |
|
|
|
x −um |
|
|
|
2 = |
|
|
|
um −un |
|
|
|
2 + 4 |
|
x − |
um + un |
|
|
|
|
2 |
|
|
|
um −un |
|
|
|
2 + 4d 2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≥ |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
16

поскольку элемент v = um 2+ un L и
|
|
|
|
|
|
|
|
|
|
ρ(x,ν) = |
|
|
|
|
x −v |
|
|
|
≥ inf |
|
|
|
|
|
|
|
x −u |
|
|
|
= d . |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Поэтому |
|
|
|
|
|
|
|
um −un |
|
|
|
2 ≤ 2 |
|
|
|
x −un |
|
|
|
|
2 + 2 |
|
|
|
x −um |
|
|
|
2 − 4d 2 , |
|
|
и |
тогда |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
2 |
|
|
|
|
1 |
2 |
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
um − un |
|
|
|
|
|
|
≤ 2 d + |
|
|
|
+ 2 d |
+ |
|
|
|
− 4d |
|
|
|
|
|
≤ 4 d + |
|
|
− 4d |
|
= |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
||||||||||||
= |
8d |
+ |
4 |
< |
|
|
|
8d + 4 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где N=min(n,m). |
|
|
|
|
||||||||||||||||||||||||||
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
N 2 |
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Величину 
 um − un
um − un 
 можно ограничить как угодно малым значени-
можно ограничить как угодно малым значени-
ем за счет надлежащего выбора числа N, т.е. последовательность {uk} – фундаментальна, и вследствие полноты H lim uk = y H . А поскольку
сходящаяся последовательность {uk} L и L – подпространство (т.е. замкнутое множество), то верно также: y L. Тогда ρ(x, y) = d , и суще-
ствование ЭНП доказано.
Покажем, что ЭНП y – единственный. Допустим противное. Пусть
~
наряду с y существует также другой ЭНП y L , т.е.
ρ( x, L) = |
|
x − y |
|
= |
|
|
|
~ |
|
= d , причём |
~ |
≠ y . На основании равенства |
|
|
|
|
|
||||||||
|
|
|
|
|
x − y |
|
y |
параллелограмма и аксиомы треугольника для нормы получаем:
|
4d |
2 |
= 2 |
|
x − y |
|
2 |
+ 2 |
|
~ |
|
|
|
2 |
= |
|
|
|
~ |
|
|
|
2 |
+ |
|
|
|
|
|
|
|
~ |
|
|
|
2 |
≤ |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x − y |
|
|
|
|
|
y − y |
|
|
|
|
(x − y) + (x − y) |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
≤ |
|
|
|
~ |
|
|
|
2 |
+ ( |
|
x − y |
|
+ |
|
~ |
|
|
|
2 |
|
|
|
|
|
|
~ |
|
|
|
2 |
+ 4d |
2 |
, |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
y − y |
|
|
|
|
|
|
|
x − y |
|
|
|
) = |
|
|
y − y |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
отсюда |
|
~ |
|
|
|
2 |
|
= 0 и |
|
|
~ |
, т.е. ЭНП – единственный. ► |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
y − y |
|
|
|
|
|
y = y |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
Теорема 6. Пусть L – подпространство в гильбертовом пространстве H, y L – ЭНП для произвольного элемента x H. Тогда любой элемент u L ортогонален элементу v=x-y: v u, что обозначают также v L.
◄ Допустим противное, т.е. u L: <x-y,u>=σ≠0. Тогда u≠θ, и (см. аксиому 1° скалярного произведения) <u,u> >0. Рассмотрим элемент
~ |
|
σ |
~ |
|
|
y |
= y + |
|
u , который также лежит в подпространстве L: |
y |
L , |
< u,u > |
|||||
т.к. y L, u L. Имеем:
17
~ 2 |
|
|
σ |
σ |
|
x − y |
= |
(x − y) − |
< u,u > u, (x − y) − |
< u,u > u |
= |
=< x − y, x − y > −2 x − y, |
|
|
σ |
|
|
u + |
|
|
|
|
σ |
u, |
|
|
σ |
u = |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< u,u > |
|
|
|
|
< u,u > |
|
< u,u > |
|
|
|
|
|||||||||||
= |
|
x − y |
|
|
|
|
2 |
− |
|
2σ |
< x − y,u |
> + |
|
σ 2 |
|
|
|
|
< u,u >= |
|
x − y |
|
2 |
− |
σ 2 |
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
< u,u > 14243 |
|
< u,u |
>2 |
|
|
|
|
|
|
|
|
< u,u > |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ 2 |
|
|
|
|
~ |
|
|
|
2 |
|
|
|
|
|
|
2 |
и y не является ЭНП. Полу- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Поскольку |
< u,u > |
>0, то |
x − y |
|
|
|
|
|
< |
x − y |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
чили противоречие, поэтому u L: <x-y,u>=0. ► |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Следствие из теорем 5,6. Пусть L – подпространство в H. Тогда x H
существует |
единственное разложение x=y+z, |
где y L |
– ЭНП, |
а z L. |
|
|
|
◄ В силу единственности ЭНП y элемент |
e3 |
|
|
z=x–y также единственный, z L. ► |
|
||
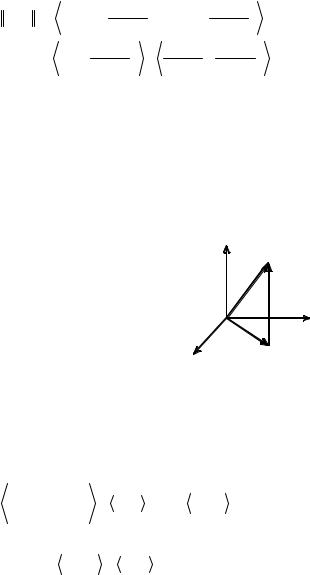
ЭНП y L называют также проекцией |
x |
v=x-y |
|
элемента x H на подпространство L. Для |
|
|
|
простейшего случая H=E3, L=E2 результат |
|
e2 |
|
теоремы 6 |
хорошо известен и имеет не- |
|
|
сложную геометрическую интерпретацию e1 |
y |
(см. рис.). |
|
Теорема 6 определяет способ нахождения ЭНП для x H в случае конечной размерности подпространства L с заданным (не обязательно
|
|
|
|
n |
ортогональным) базисом {g1, g2 ,K, gn } в виде y = ∑λj g j . Поиск ко- |
||||
эффициентов разложения {λj }nj=1 |
|
|
j=1 |
|
осуществляется следующим образом. |
||||
Так как k: gk L, <x-y,gk>=0, то |
|
|
|
|
n |
|
|
|
n |
x − ∑λj g j , gk |
= x, gk |
− |
∑λj g j , gk = 0 , |
|
j=1 |
|
|
|
j=1 |
или |
|
|
|
|
n |
|
|
|
|
∑λj g j , gk |
= |
x, gk |
, |
(5) |
j=1 |
|
|
|
|
k =1,K, n. |
|
|
||
18 |
|
|
|
|
Определитель полученной системы линейных уравнений есть определитель матрицы Грама G = {< g j , gk >}kn, j=1 , причём detG≠0 в силу линейной независимости элементов {g1 , g2 ,K, gn }. (Напомним, что detG=0 тогда и только тогда, когда элементы {g1 , g2 ,K, gn } линейно зависимы.) Таким образом, система уравнений (5) имеет единственное решение –
набор коэффициентов {λj }nj=1 |
n |
, который задает ЭНП y = ∑λj g j . |
|
|
j=1 |
Если же элементы базиса подпространства {g1 , g2 ,K, gn } L не только линейно независимы, но и ортогональны, то поиск коэффициентов {λj }nj=1 упрощается (убедитесь самостоятельно):
λj = |
< x, g j > |
. |
(6) |
|
< g j , g j > |
||||
|
|
|
Определение. Пусть L – подпространство в H. Совокупность всех элементов из H, ортогональных к L, L ={x H | x L} , называется
ортогональным дополнением подпространства L.
Теорема 7. |
Пусть L – подпространство в гильбертовом |
|
пространстве H. Тогда L также является подпространством в H. |
||
◄ Нужно доказать, что L – замкнутое линейное многообразие. |
||
Линейность. |
u L, x,y L |
z=αx+βy: |
|
<u,z>=<u,αx+βy>=α<u,x>+β<u,y>=0. |
|
То есть для любой линейной комбинации z=αx+βy элементов из L : z L, следовательно, z L и L – линейное многообразие.
Замкнутость. Возьмем произвольную сходящуюся последовательность {zn} L , и покажем, что предельная точка limzn=z L . Имеем u L: <u,zn>=0, но в силу непрерывности скалярного произведения (лемма 2)
lim <zn,u>=<z,u>=0. Следовательно, z L и множество L содержит все
n→∞
свои предельные точки, т.е. замкнуто. ►
Определение. Будем говорить, что гильбертово пространство H разлагается в ортогональную сумму подпространств L1,L2,…,Ln и записывать это как H=L1 L2 … Ln, если:
19

1) Все подпространства L1,L2,…,Ln попарно ортогональны, т.е.
u Li, v Lj: <u,v>=0, если i≠j.
n
2) x H существует разложение x = ∑xi , где xi Li.
i =1
Теорема 8. Пусть в гильбертовом пространстве H задано конечномерное подпространство L с ортогональным базисом {g1 , g2 ,K, gn }, а
n
y = ∑λj g j – ЭНП для произвольного элемента x H. Тогда для «векто-
j=1
ра-ошибки» x-y:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
x − y |
|
2 = |
|
x |
|
2 |
− |
|
y |
|
2 = |
|
x |
|
|
2 |
− ∑λ2j |
|
|
|
|
g j |
|
2 . |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
◄ В |
соответствии с теоремой 6 |
j =1,K,n : |
|
x − y, g j |
= 0 и |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
y, g j |
= x, g j |
|
= λj g j , g j |
|
|
(см. (6)). Далее, в силу ортогональности |
||||||||||||||||||||||||||||||||||||||||||
базиса {g1, g2 ,K, gn }: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
x − y |
|
|
|
=< x − ∑λj g j , |
x − ∑λj g j >= |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
j=1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
2 , |
|
|||||||
=< x, x > −2∑λj < x, g j > + |
∑λ2j |
|
|
< g j , g j > = |
|
|
|
x |
|
|
|
|
2 − ∑λ2j |
g j |
|
причем |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
n |
|
n |
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
2 . ► |
|||||||||||||||||
|
|
|
y |
|
|
|
2 =< ∑λj g j , ∑λm gm >= ∑λj ∑λm < g j , gm >= ∑λ2j |
g j |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
j=1 |
|
m=1 |
j=1 |
|
|
m=1 |
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|||||||||||||||||
Пусть теперь в H задана бесконечная последовательность ненуле-
вых ортогональных векторов {ϕk }∞k =1 H . (Это означает также, что H – бесконечномерно, так как ортогональные элементы линейно независи-
мы.) Рассматривая первые элементы {ϕ |
}n |
как базис, получаем неко- |
||
|
k k =1 |
|
|
|
торое линейное многообразие Ln, «натянутое» на {ϕ |
}n |
. Можно пока- |
||
|
|
|
k k =1 |
|
зать, что Ln – замкнуто, т.е. является подпространством. Так как Ln –
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
конечномерно, то верна теорема 8 и для ЭНП yn = ∑λjϕ j , |
yn Ln : |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
2 = |
|
|
|
2 − |
|
|
|
2 |
|
|
|
|
2 |
n |
2 . |
|
|||
|
|
x − yn |
|
|
x |
|
|
yn |
|
= |
|
x |
|
− ∑λ2j |
|
ϕ j |
|
(7) |
|||||
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
