Добавил:

korayakov Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

Математическое обеспечение цифровой обработки и кодирование сигналов

Файл:

книжка умняшкина по моцос

.pdf

Скачиваний:

133

Добавлен:

16.04.2013

Размер:

1.55 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 185 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

∞

(∆ν)2 (∆t)2 =

∫

(f ′(t))2 dt ∫t2

(f (t))2 dt =

f ′(t)

tf (t)

2 ,

(2π )

−∞

(2π )

где в пространстве L2(R) норма вещественной функции индуцирована

∞

скалярным произведением (см. раздел 1.5) < f (t), g(t) >= ∫ f (t)g(t)dt .

−∞

Так как на основании неравенства Коши-Буняковского (лемма 1.1)

∞

f ′(t) 2 tf (t) 2 ≥ f ′(t), tf (t) 2 =

∫ f ′(t)tf (t)dt ,

то

−∞

∞

t =∞

∆ν∆t ≥

∫ f ′(t)tf (t)dt

t(f (t))

t =−∞ −

∫

(f (t)) dt

2π

4π

−∞

14243

−∞

14243

поскольку

силу

существования

конечного

интеграла

(∆t)2 = ∞t2

f (t)

2 dt :

lim t2 (f (t))2

= 0 , откуда и

lim t(f (t))2 = 0 . ►

∫

t→±∞

→±∞

−∞

Задание. Убедитесь, что для сигнала с энергией

E = ∫−+∞∞

f (t)

2 dt оценка

(10) принимает следующий общий вид: ∆t∆ν ≥ E 4π .

Пример 2. Покажем, что минимальное значение величины (10) дает гауссов импульс, т.е. функция вида f (t) = C e−kt 2 , где C, k – некоторые

константы (k>0).

∞

◄ Для существования интеграла (∆ν )2 = ∫t2 f (t) 2 dt , очевидно, необ-

−∞

ходимо положить k>0. Для построения рассуждений достаточно рассмотреть случай единичной энергии сигнала, положив C = 4 2k π (убе-

∞

дитесь, что в этом случае энергия сигнала единичная, ∫ f (t) 2 dt =1 ,

−∞

воспользовавшись равенством ∫−+∞∞exp(−t2 / 2)dt = 2π ). Для упрощения

выкладок проведём доказательство только для k=1/4, т.е. для легко обобщаемого (с использованием свойства 3° преобразования Фурье) на

другие значения k>0 случая		f (t) =	1	e	−(t 2	4)	. Поскольку
другие значения k>0 случая		f (t) =	4 2π	e			. Поскольку
			4 2π
1	∫−+∞∞ t2 exp(−t2 / 2)dt =1 (как выражение для дисперсии стандартного
2π

нормального закона), то и для эффективной длительности сигнала во

+∞

2 dt =1 , т.е. ∆t=1.

временной области также получаем (∆t)2 = ∫t2

f (t)

−∞

Для спектральной плотности имеем:

d (e

′

+∞ −(t

2 4) −2πiνt

(−2πit)dt =

4πi

+∞

−2πiνt

−t 2

S (ν)

2π

∫e

2π

∫e

−∞

= 44πi

t=∞

+∞

e−2πiν t−(t2

− ∫e−t2

4 (−2πiν) e−2πiνt dt

= −8π

2νS(ν) .

t=−∞

2π 1442443 −∞

0−0

Отсюда

получаем

следующее

дифференциальное

уравнение:

(ln S(ν))′ = −8π 2ν , интегрируя которое,

находим:

S(ν) = N e−4π 2ν 2 ,

где

нормировочная

константа N определяется из

равенства

Парсеваля:

+∞

N 2

+∞ −(4πν )2

1 = ∫ f (t)

2 dt = ∫ S(ν)

2 dν =

∫ e

d (4πν) = N 2 8π . Оконча-

−∞

4π

−∞

144424443

2π

тельно, получаем спектральную плотность S(ν) = 4 8π e−4π 2ν 2

. Тогда для

эффективной полосы имеем

+∞

8π

+∞

(∆ν)2 = 8π ∫ν2 e−8π 2ν

2 dν =

2 ∫(4πν)2 e−(4πν )2 2 d(4πν)

4π(4π)

(4π)

−∞

14444244443

2π

Отсюда ∆ν =14π и ∆ν∆t =14π . ►

Заметим, что для сигнала любой формы его «сжатие» по аргументу во временной области приводит к такому же масштабному «расширению» по аргументу в частотной области, см. свойство 3° преобразования

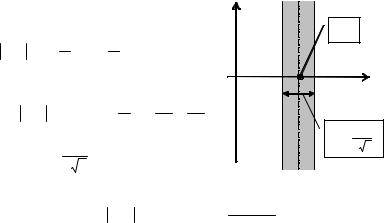
Фурье. Таким образом, чем меньше ширина полосы сигнала, тем выше его длительность, и наоборот. Построив прямоугольную систему координат, осями которой являются время и частота, каждому сигналу на полученной плоскости «Время×Частота» можно будет поставить в соответствие некоторую прямоугольную область Ω локализации сигнала, со сторонами ∆t и ∆ν. При этом, если понимать ∆t и ∆ν в смысле эффективных значений, то для сигнала единичной энергии площадь данной области в соответствии с принципом неопределенности не может быть меньше величины 1/4π.

Пример 3. Изобразить на плоскости «Время×Частота» область локали-

зации Ω=∆t×∆ν сигнала из примера 1 для эффективных значений полосы

и длительности (8), (9).

◄ Во временной области получаем среднее

значение

распределения

энергии:

Ω

T/2

∞

m =

∫

t f (t)

dt =

∫

tdt

, а

для

эффек-

−∞

тивной длительности:

(∆t)2 = ∞t2 f (t) 2 dt −m 2

= T t2 dt − T 2

= T 2

∫

−∞

∆t =

∆t = T .

т.е.

2 3

В частотной области

(∆ν )2 = lim

sin

πνT2 dν → ∞ ,

∫ν 2 S(ν) 2 dν = lim

∫ ν 2

F →∞

−F

F →∞

−F

T (πν)

т.е. эффективная полоса сигнала ν (− ∞;∞). Область Ω=∆t×∆ν отражена на рисунке. ►

2.4. Энергетический спектр. Спектр мощности

Корреляционной функцией (КФ) сигнала f(t) назовем интеграл (если он существует):

+∞
R(τ) = ∫ f (t) f (t −τ)dt .	(11)

−∞

Корреляционная функция характеризует «степень сходства» сигнала и его сдвига по аргументу: чем больше значение КФ, тем это сходство выше. Так, максимальное «сходство» наблюдается при τ=0, когда значение корреляционной функции максимально и равно энергии сигнала,τ : R(τ)≤R(0)=E. Действительно, понимая под скалярным произведением функций f(t), g(t) (элементов пространства L2(R), см пример 1.7) ве-

+∞

личину < f , g >= ∫ f (t)g(t)dt ,

на основании неравенства Коши-

−∞

Буняковского получаем для КФ τ :

R(τ) = f (t), f (t −τ) ≤ R(τ) = f (t), f (t −τ) ≤

≤

f (t)

f (t −τ)

f (t)

2 = R(0) ,

так как

+∞

τ :

f (t −τ)

= ∫ f (t −τ)2 dt = ∫ f (t)2 dt = f (t) = R(0) .

−∞

То есть максимальное значение, равное энергии сигнала, КФ (11) принимает при значении аргумента, равном нулю.

Задание. Убедитесь самостоятельно, что КФ – четная функция.

Найдем преобразование Фурье для КФ.

+∞ +∞

−2π iντ

+∞

2π iντ

∫ f (t) f (t −τ)dt

dτ = ∫

∫ f (τ − t) e

dτ

Φ(R(τ)) = ∫

f (t)

−∞

+∞

e−2π iνt

2 .

= ∫ f (t)

S f (ν)

dt =

S f

(ν)

S f (ν) =

S f (ν)

(12)

−∞

Получили, что преобразование Фурье КФ представляет собой квадрат модуля спектральной плотности сигнала. Выражение (12) называется

энергетическим спектром сигнала.

Если функция f(t) является периодической и интеграл по периоду T:

T		2 dt = C ≠ 0 ,
∫	f (t)		то,	очевидно,	энергия	сигнала
∫	f (t)		то,	очевидно,	энергия	сигнала
0
44

	N		2 dt → ∞ и интеграл (11) не существует. Для периодиче-
E = lim	∫	f (t)

N →∞
	−N

ских сигналов f(t) под КФ вместо (11) понимают функцию (заметим, также имеющую период Т)

	1	T / 2
R(τ) =		∫ f (t) f (t −τ)dt .	(13)
	T
		−T / 2

Тогда R(0) представляет собой среднюю энергию сигнала за единицу времени, т.е. мощность.

Задание. Убедитесь самостоятельно, что КФ (13) – также четная функ-

ция и R(τ) ≤ R(0) .

Для стационарного, не обязательно периодического, случайного процесса (сигнала) X(t) корреляционной функцией называем математическое ожидание КФ (13), т.е.

R(τ) = M(X (t) X (t −τ)).

Напомним, понятие стационарности означает неизменность статистических характеристик процесса во времени, поэтому корреляционная функция случайного процесса зависит только от расстояния τ между сечениями процесса по оси времени, но не от самого момента наблюдения t. Если стационарный процесс является эргодическим, то математическое ожидание (среднее по всем возможным реализациям процесса, число которых бесконечно велико) можно понимать как усреднение по единственной реализации процесса:

R(τ) = M(X (t) X (t −τ))= lim	1	+T / 2
		∫x(t)x(t −τ)dt .

T →∞
	T −T / 2

Тогда, по аналогии с (12), можем получить для эргодического процесса:

Φ(R(t)) = lim	S f (ν)	2	(14)
	S f (ν)	2

	T
T →∞	T

- называем данную функцию частоты спектром мощности. Соотноше-

ние (14) носит название теоремы Винера-Хинчина.

Глава 3. Дискретизация и квантование сигналов. Дискретные ортогональные преобразования

3.1. Преобразование непрерывных сигналов в дискретные

Под термином сигнал мы традиционно понимаем физический процесс (например, изменяющееся во времени напряжение), отображающий некоторую информацию (сообщение). Математически сигнал описывается функцией f(t) определённого вида. Характеризовать виды сигналов будем с использованием следующих понятий.

Аналоговый сигнал – описывается непрерывной (или кусочнонепрерывной) функцией f(t), которая может принимать любые конечные значения.

Дискретный сигнал – это функция дискретного аргумента y=y(nT) с областью определения D = {nT n Ζ}. Значения y(nT) называются от-

счётами дискретного сигнала, а величина Т, представляющая собой расстояние по оси аргумента между соседними отсчётами, называется интервалом дискретизации. Будем использовать также обозначения y(nT)=y(n)=yn. Таким образом, дискретный сигнал описывается последовательностью отсчётов {yn}. Последовательность может быть и конечной, тогда будем использовать запись вида y(n)={y0,y1,…,yN}, например y(n)={0,1/2,-0.7,1}.

Под цифровым сигналом понимаем дискретный сигнал, который может принимать значения из конечного множества чисел, n y(n) {h1,…,hM}. Возможные значения сигнала hj (j=1,…,M) называем

уровнями квантования сигнала.

Реальные физические процессы почти всегда описываются аналоговыми сигналами f(t), причем интервалы наблюдения – конечны, t [a,b]. Для последующей цифровой обработки аналоговый сигнал, прежде всего, необходимо преобразовать в дискретный. Для этого, в простейшем случае, из аналогового сигнала f(t) производится равномерная выборка с шагом дискретизации T=∆t: fn=y(a+n∆t), n=0,1,…,N. Для восстановления непрерывного (аналогового) сигнала по выборке {f0,f1,…,fN} чаще всего используются интерполяционные методы, например, восстановленный сигнал можно представить в виде степенного интерполяционного мно-

гочлена	~	N	~	N

	f (t) = ∑ak tk , или в более общем виде как		f (t) = ∑ckϕk (t) ,
		k =0		k =0

где {ϕk(t)} – некоторая система функций на отрезке t [a;b].

При дискретизации сигнала в первую очередь возникает вопрос: каким выбирать шаг аргумента ∆t, т.е. как часто нужно брать отсчёты для формирования выборки {fi}? Очевидно, что для сокращения объёма данных и, соответственно, упрощения обработки, не следует выбирать отсчёты слишком часто, т.е. шаг дискретизации ∆t нужно сделать по возможности бóльшим. С другой стороны, увеличивая ∆t, мы можем

неадекватно описать исходный аналоговый	сигнал	через дискретное
представление, т.е. получим неприемлемую	ошибку		~	для

			f (t) − f (t)

восстановленного сигнала f (t) .

Для того, чтобы сформулировать критерий для выбора величины шага дискретизации ∆t, необходимо задаться какими-либо ограничениями, накладываемыми на функцию f(t).

3.2. Дискретизация по критерию наибольшего отклонения

Для заданного способа R восстановления непрерывного сигнала по

дискретному,	~
	f (t) = R{ fn } , можно сформулировать задачу выбора шага

дискретизации ∆t для формирования отсчётов fn=f(tn), tn =a+n∆t, в следующем виде: выбрать по заданному уровню ошибки ε0 шаг ∆t так,

чтобы

< ε0 .

(1)

f (t) − f (t)

В качестве нормы в (1) обычно

берется максимум

отклонения,

ε(t)

= max

ε(t)

, а для восстановления непрерывного сигнала

f (t) по

t [a;b]

дискретному {fn} используются степенные интерполяционные многочлены. Известно, что по n+1 точкам {(tk , fk )}kk ==0n можно построить единственный интерполяционный многочлен n-ой степени,

, а для ошибки интерполяции верно:

f (t) = Pn

(t) = ∑ak t

k =0

n +1

∏(t − tk )

(2)

ε(t)

f (t) − f (t)

≤

(n +1)!

k =0

M n+1

ε(t)

= max

ε(t)

≤

max

∏(t −tk )

(3)

t [a;b]

(n +1)! t [a;b]

k =0

где M n+1

= max

f (n+1) (t)

– максимум модуля (n+1)-ой производной.

t [a,b]

Задание большого числа узлов интерполяции (т.е. высокой степени интерполяционного полинома) нередко влечет недопустимые для практических приложений задержки восстановления аналогового сигнала: поскольку для построения интерполяционного полинома требуется знание всех отсчётов сигнала, то задержка времени восстановления не может быть меньше T=n∆t. Кроме того, повышение порядка интерполяции (т.е.степени используемого интерполяционного полинома) влечёт и увеличение объёма необходимых вычислений, ужесточая аппаратурные требования. По этим причинам на практике обычно используются интерполяторы не более чем третьего порядка.

Итак, положим, что восстановление аналогового сигнала происходит с использованием степенного интерполяционного полинома. Тогда на основании формул (1) и (3) получаем следующий критерий выбора шага дискретизации:

	n		(n +1)!
max	∏(t −tk )	≤		ε0 .	(4)

t [a;b]	k =0		M n +1

Для использования данного критерия необходимо знать оценку максимума модуля (n+1)-ой производной интерполируемого сигнала.

Пример 1. Пусть для восстановления сигнала используется линейная

интерполяция,

т.е.

порядок

полинома

n=1. Известно значение

M2 =

max

′′

, и

задано ограничение

на ошибку восстановления

(t)

t (−∞;∞)

< ε0

сигнала: max

. Каким следует выбрать шаг дискрети-

f (t) − f (t)

t (−∞;∞)

зации ∆t?

◄ Все участки линейной интерполяции [tk,tk+1] имеют одинаковую длину, равную ∆t=tk+1–tk, и для каждого такого участка должно выполняться

неравенство (4):

max

(t − tk )(t − tk +1 )

≤

M 2

t [tk ;tk +1 ]

(∆t)2

(t −tk )(t −tk +1)

k +1

−t

то

max

t [tk ;tk +1 ]

ε0 .		Так как
∆t ≤	8ε0	. ►
	M 2

3.3. Частотный критерий выбора шага дискретизации

Прежде чем формулировать соответствующий критерий для выбора шага дискретизации ∆t, рассмотрим следующий пример.

Пример 2. «Эффект наложения частот». Рассмотрим два аналоговых

сигнала, представляющих собой гармонические колебания:

ϕ1(t) = cos(π(β +α)t +γ ), ϕ2 (t) = cos(π(β −α)t −γ ), где α, β, γ – любые вещественные числа. Тогда выбрав шаг дискретизации ∆t=1/β, мы не сможем по отсчётам в точках tk=k∆t, k Z, отличить сигналы ϕ1(t) и ϕ2(t),

хотя гармонические колебания имеют различные частоты: ν1 = β +2 α ,

ν	2	=	β −α	( ω = π(β +α) ,		ω =π(β −α) ).

		2		1		2
					x + y			y − x
◄ Так как				cos x −cos y = 2sin			sin		, то для отсчётов в точках
								2
				2
tk=k∆t=k/β				имеем: ϕ2 (tk ) −ϕ1		(tk ) = 2sin(πβtk )sin(παtk +γ )= 0 . ►
								14243

sinπk =0

Если спектр S(ν) функции f(t) имеет финитный (т.е. конечный) носитель, то ответ на вопрос о выборе величины шага дискретизации ∆t даёт теорема отсчётов, известная в отечественной литературе как теорема Котельникова, а в зарубежной – как теорема Найквиста или теорема Шеннона.

Теорема 1. (Теорема отсчётов.) Если f(t) имеет спектр ограниченной частотной полосы, т.е. S(ν)=0 при ν > F , то функция f(t) может быть

точно восстановлена по своим значениям в точках tk=k∆t (k Z), где

∆t =	1	, при помощи формулы:
	2F		sin(2πF(t −k∆t))
		∞

		f (t) = ∑ f (k∆t)		.

		k =−∞	2πF(t −k∆t)

◄ Выразим функцию через её спектр, f (t) = ∫S(ν

−F

(5)

) e2πiνt dν , тогда с

использованием обозначения ∆t = 21F получим k Z:

F 2πiνk

f (k∆t) = ∫S(ν) e 2F dν .

−F

Спектральную плотность S(ν), принимающую ненулевые значения только на отрезке ν [-F;F], периодически продолжим (с периодом 2F) на

всю ось частот, и полученную в результате функцию

представим в

S (ν)

виде ряда Фурье (2.3):

∞

−2πi

kν

∑ck e 2F

∫S(ν) e 2F

S (ν) =

где

ck =

dν .

k =−∞

−F

Сравнивая полученную запись с выражением для

f (k∆t) , видим, что

ck =

f (−k∆t) . Тогда

~	1	∞
S (ν) =		∑ f (−k∆t) e

	2F k =−∞

f (t) = ∫S(ν) e2πiνt dν =

−F

2πi	kν =		1	∞
2F			1	∑ f (k∆t) e−2πiνk∆t ,
2F				∑ f (k∆t) e−2πiνk∆t ,
			2F k =−∞
1		F	∞			2πiνt
			∑ f (k∆t) e		−2πiνk∆t	2πiνt
		∫			e		dν .
2F		∫			e		dν .
2F		−F k =−∞

Меняя в последнем выражении порядок интегрирования и суммирования, имеем:

	1	∞		F
f (t) =		∑	f (k∆t)	∫e2π iν (t−k∆t) dν	.

	2F k =−∞			−F

Отсюда, учитывая, что ∫e2πiν (t−k∆t)

−F

dν	=	sin(2πF(t − k∆t))	, получаем
		π(t − k∆t)

утверждение теоремы. ►

Таким образом, при помощи формулы (5) для функции ограниченного спектра можно найти её точное значение в любой точке числовой оси t (-∞;∞), по отсчётам fk=f(tk) в точках tk=k∆t, которые полностью определяют функцию. Формула (5) представляет собой функциональный

∞
ряд f (t) = ∑λkϕk (t) по системе функций
k =−∞		(t) = sin(2πF(t − k∆t))
ϕ	k	(t) = sin(2πF(t − k∆t))		,
	k	2πF(t − k∆t)
		2πF(t − k∆t)	k Ζ

представляющих собой сдвиги по оси абсцисс на величину k∆t = k2F

функции ϕ0 (t) =ϕ(t) = sin 2πFt . Базисные функции {ϕk} обращаются в

2πFt

ноль во всех точках tm=m∆t (m Z), за исключением точки tk=k∆t, для ко-

<<< < Предыдущая 1 2 3 45 / 185 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>