Добавил:

korayakov Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

Математическое обеспечение цифровой обработки и кодирование сигналов

Файл:

книжка умняшкина по моцос

.pdf

Скачиваний:

133

Добавлен:

16.04.2013

Размер:

1.55 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1810 11 12 13 14 15 16 17 18 > Следующая >>>

N		1
H (z) = ∑bk z	−k	1		.
H (z) = ∑bk z	−k	M		.
k =0		1 + ∑am z	−m
14243		1 + ∑am z
H1 ( z)		m=1
		1442443

x(n) v(n)

H2(z) H1(z)

функциям H2(z), H1(z) соответствуют разностные уравнения:

v(n) = x(n) − ∑amv(n −m) ,

m=1

y(n) = ∑bk v(n −k) .

k=0

Вфильтрах, реализующих данные разностные уравнения, как видим, имеет место только задержка сигнала v(n), поэтому возможно использовать только один набор элементов задержки, что позволяет построить структурную схему фильтра, изображенную на рисунке справа, где

L=max(N,M).

z-1

-0.4 3

z-1

	H2 ( z)					V(z)=H2(z)X(z),
	Обозначим					V(z)=H2(z)X(z),
y(n)	Y(z)=H1(z)V(z), что					соответствует
	структурной схеме					последователь-
	ного соединения, изображенной на
	рисунке			слева.		Передаточным

x(n)			v(n)			b0	y(n)

			z-1
		-a1				b1
		-a1		v(n)		b1

			z-1
		-a2			n-1)	b2
		-a2		v(	n-1)	b2

-aL-1 v(n-L+1) bL-1

z-1

-aL v(n-L) bL

Пример 11. Построить прямую каноническую форму структурной схемы для фильтра из примера 10.

◄ Проделайте самостоятельно, результат см. на рисунке слева. ►

Если в разностном уравнении (8) отсутствует зависимость отсчёта выходной последовательности y(n) от предыдущих остчётов y(n-k) (k≥1),

N		N
т.е. y(n) = ∑bk x(n −k) и		H (z) = ∑bk z−k , то, очевидно, соответствую-
k =	0	k =	0

щий фильтр будет КИХ-фильтром, импульсная характеристика которого: h(n)={b0,b1,…,bN,0,0,…}. Такие фильтры не имеют в структурной схеме обратной связи и являются нерекурсивными. БИХ фильтры могут быть только рекурсивными, т.е. фильтрами с обратной связью, и в разностном уравнении (9) по крайней мере один коэффициент am≠0. Однако наличие обратной связи ещё не говорит о том, что фильтр имеет бесконечную импульсную характеристику.

Пример 12. Найти передаточную функцию, им-	z-1	-1
пульсную характеристику и упростить структур-
пульсную характеристику и упростить структур-
ную схему фильтра, изображенного на рисунке

справа.

◄ Убедитесь самостоятельно, что H(z)=1,

h(n) = δ~(n) .

►

z-1

Нерекурсивные фильтры всегда являются фильтрами с КИХ. Синтезировать КИХ-фильтр по заданной ИХ h(n)={h(0),h(1),…,h(N),0,0,…}

очень просто, для этого нужно выбрать коэффициенты {bk = h(k)}kN=0 .

Синтез рекурсивных фильтров более сложен, однако при аппроксимации импульсных характеристик (в том числе, конечных ИХ) использование рекурсивных схем фильтров часто позволяет приближенно реализовать заданную ИХ меньшим количеством элементов задержки и умножителей. Для анализа и синтеза фильтров важным является вопрос их устойчивости.

4.4. Устойчивость ЛДФ

Определение. ЛДФ называется устойчивым, если при любой ограниченной последовательности x(n) ( x(n) ≤ C1 < ∞ ), поданной на вход фильтра, выходная последовательность также ограничена, т.е. y(n) ≤ C2 < ∞ .

В неустойчивой системе при каких-то ограниченных входных сигналах выходной сигнал может неограниченно возрастать.

Теорема 3. Необходимым и достаточным условием устойчивости ЛДФ является ограниченность суммы

∞
∑h(n) ≤ C < ∞.	(11)

n=0

◄Докажем сначала достаточность выполнения условия (11) для устойчивости ЛДФ. При поступлении на вход ЛДФ произвольного ограни-

ченного воздействия x(n), x(n) ≤ C1 < ∞ , получаем на выходе n:

y(n)

∑x(n −k)h(k)

≤ ∑

x(n −k)

h(k)

≤ C1

∑

h(k)

≤ C1C < ∞ .

k =0

То есть выходная последовательность ограничена, фильтр устойчив. Докажем теперь необходимость выполнения условия (11) для ус-

тойчивости ЛДФ. Допустим противное: фильтр устойчив, но (11) не вы-

полняется, последовательность частичных сумм S j = ∑j			h(n)	неограни-
полняется, последовательность частичных сумм S j = ∑j			h(n)	неограни-
		n=0
ченно возрастает с увеличением номера j. То есть			С>0	J=J(C):
J
∑	h(n)	> C . Выбрав такой номер J по произвольному как угодно боль-
∑	h(n)
n=0

шому значению С>0, рассмотрим реакцию ЛДФ на следующее (ограниченное!) входное воздействие, которое строится по ИХ данного ЛДФ:

приh(J −n) ≥ 0

x(n) =

приh(J −n) < 0

−1

В выходной последовательности получаем

y(J )

∑x(n)h(J −n)

= ∑

h(J −n)

= ∑

h(n)

> C .

n=0

Таким образом, для как угодно большого значения C можно подобрать ограниченное входное воздействие, при котором существует элемент

y(J) выходной последовательности, для которого y(J ) > C , т.е. фильтр

не является устойчивым. Следовательно, предположение о том, что для устойчивого ЛДФ условие (11) может не выполняться – ложно. ►

Следствие 1. Необходимое условие устойчивости ЛДФ: lim h(n) = 0 .

n→∞

Следствие 2. КИХ-фильтры всегда устойчивы.

Пример 13. При каких значениях параметра a фильтр из примера 4 является устойчивым?

◄ При решении примера 4 было установлено, что для данного фильтра

∞

ИХ h(n) = an . Условие (11) принимает вид: ∑ a n < ∞. Отсюда a <1.►

n=0

Выполнение условия (11) часто трудно проверить, тогда используется также другой критерий устойчивости.

Теорема 4. Для того чтобы ЛДФ был устойчив, необходимо и достаточно, чтобы все полюсы передаточной функции H(z) лежали на комплекс-

ной плоскости внутри единичного круга: z <1 .

◄ Как отмечалось ранее, передаточные функции ЛДФ можно представить в виде отношения конечных степенных многочленов, H(z)=P(z)/Q(z), поэтому особыми точками передаточной функции являются полюсы (конечное число), которые определяются нулями многочлена Q(z).

1. Необходимость. Так как фильтр устойчив, то для

≥1 передаточная

∞

функция ограничена:

H (z)

∑h(n)z−n

≤ ∑

h(n)

z−n

≤ ∑

h(n)

< C .

n=0

Следовательно, в области z ≥1 у передаточной функции нет полюсов.

2. Достаточность. В соответствии с (4) ИХ h(n) =	1	∫H (z)zn−1dz , где γ
	2πi	γ
		γ

– замкнутый контур, охватывающий все особые точки подынтегральной функции. Особые точки подынтегральной функции – полюсы конечного порядка – могут быть лишь в нулях многочлена Q(z), а при n=0, возмож-

но,	и в точке z=0. Так как число нулей {zk				Q(zk ) = 0}kL=1 конечно, то


r	= max	z	k	, причём r1<1. В качестве контура интегрирования γ, охва-

1	k =1,...,L

тывающего все особые точки функции H (z)zn−1 , возьмем окружность

γ = {z = r}, где r = 1+2r1 <1 . На этой окружности Q(z)≠0, передаточная

функция

не имеет полюсов

и потому

ограничена, т.е. M<∞:

H (z)

≤ max

H (z)

≤ max

P(z)

min Q(z) ≤ M .

Выполняя замену

пере-

менной интегрирования z = r eiϕ ,

для ИХ получаем следующую оценку:

2π

h(n)

∫H(z)zn−1dz =

∫H(r eiϕ )irn eiϕn dϕ ≤ r

∫M eiϕn dϕ = Mrn .

2πi

2π

Поскольку r<1, получаем для условия (11):

∞

∑

h(n)

≤ M ∑rn =

< ∞ ,

т.е. ЛДФ устойчив.

►

1− r

n=0

Пример 14. Определить по передаточной функции, при каких значениях параметра a фильтр из примера 4 является устойчивым.

◄ Ранее (см. пример 8) найдено, что H (z) = z −z a . Единственная особая

точка передаточной функции – полюс первого порядка z=a. Требование теоремы 4 приводит к уже установленному в примере 13 условию устой-

чивости фильтра: a <1. ►

4.5. Частотная характеристика ЛДФ

Определение. Частотной характеристикой (ЧХ) ЛДФ назовём комплексную функцию вещественной переменной ω :

K(ω) = H (eiω ) , которую получаем при подстановке в передаточную функцию аргумента z = eiω .

Иными словами, частотная характеристика представляет собой вы-

∞

ражение K(ω) = ∑h(k) e−iωk – для устойчивых ЛДФ данный ряд схо-

			k =0					ω,	так	как
дится		абсолютно			при	любых	значениях	ω,	так	как
∞			∞
∑	h(k) e−iωk		= ∑	h(k)	≤ C < ∞ . Физический смысл частотной характе-
k =0			k =0

ристики – комплексный коэффициент передачи гармонических колебаний: K(ω) характеризует амплитуду и фазу (в установившемся режиме!)

на выходе ЛДФ при поданном на вход гармоническом колебании с циклической частотой ω и единичной амплитудой. Действительно, если входное воздействие представляет собой отсчёты комплексного гармо-

нического сигнала, а именно, x(n) = eiωn (n≥0), то найденный по формуле свёртки отклик ЛДФ получаем:

y(n) =	n	h(k)eiω(n−k )	= eiωn		n	h(k) e−iωk →K(ω) eiωn . (12)
y(n) =	∑	h(k)eiω(n−k )	= eiωn	∑		h(k) e−iωk →K(ω) eiωn . (12)
	∑	14243	{	∑		n→∞
	k =0	x(n−k )	x(n) k =0
				14243
				K	(ω) →K (ω)
				n		n→∞

То есть в установившемся режиме (при больших значениях номера n) на выходе ЛДФ получаем гармоническое колебание той же частоты, но с другой амплитудой и фазой, изменение которых определяется ЧХ: y(n)/x(n)=K(ω). Можем также записать ЧХ в показательной форме:

K(ω) = K(ω) e−iϕ(ω) . Тогда изменение амплитуды гармонического коле-

бания на выходе ЛДФ в установившемся режиме характеризуется модулем частотной характеристики, или амплитудно-частотной характери-

стикой (АЧХ) K(ω) , а фазы – фазо-частотной характеристикой

(ФЧХ) ϕ(ω)=-arg(K(ω)). Рассмотрим это на примере.

Пример 15. Определить отклик фильтра из примера 4, имеющего значе-

ние параметра a = 1 , в установившемся режиме при подаче на вход

3
последовательности x(n)={1,0,-1,0,1,0,-1,0,…}.
◄ Для данного фильтра H (z) =	z		, откуда K(ω) =				1	. Заданное
◄ Для данного фильтра H (z) =	z − a		, откуда K(ω) =			1−	e−iω	. Заданное
	z − a						e−iω
							3
							3
входное воздействие: x(n) = cos	πn			πn	. В силу линейности ЛДФ
входное воздействие: x(n) = cos	πn	= Re ei		2	. В силу линейности ЛДФ
	2

и вещественности его коэффициентов выходной сигнал y(n) будет представлять собой действительную часть отклика фильтра на комплексное

				~	i	πn
гармоническое	колебание	частоты	ω =π / 2 :			2	,
				x(n) = e
~			~	~
y(n) = Re( y(n)) . В установившемся режиме			y(n) = K(π	/ 2)x(n) . Поэто-

му для n>>1:

πn

1 −

y(n) = Re

= Re

−i

−

1 −

		πn				π
	i		3		−i			3	π n		π
				e			=			−
= Re e{						6			cos			.
		2	2					2	2		6
	~
	x (n)		14243
			K (π / 2)

Заметим, что по АЧХ и ФЧХ полученный ответ можно было записать и сразу. Так, изменение амплитуды характеризуется АЧХ и для ω =π / 2

имеем: K(π / 2) =	3	, а задержка фазы выходного сигнала определяет-
	2

ся ФЧХ: ϕ(π /2)=-arg(K(π /2))= π /6. ►

Результат примера 15 обобщается очевидным образом. Если на вход ЛДФ подается дискретное гармоническое колебание вида x(n) = Acos(ωn −γ ), то по известным АЧХ и ФЧХ отклик ЛДФ в уста-

новившемся режиме находится как y(n) = A K(ω) cos(ωn −γ −ϕ(ω)).

Однако использование данной формулы возможно лишь для достаточно больших значений индекса n, когда можно полагать (см. (12)), что

n	∞
Kn (ω) = ∑h(k) e−iωk ≈ K(ω) = ∑h(k) e−iωk . Для КИХ-фильтров		с ИХ
k =0	k =0
h(k) = {h(0), h(1),K,h(N ),0,0,K} точное равенство Kn (ω) = K(ω)		полу-

чаем для значений n≥N. Для устойчивых БИХ-фильтров h(k) →0

k →∞

и бесконечную ИХ фильтра с некоторым приближением также можно считать конечной, выбрав достаточно большое число N: KN (ω) ≈ K(ω) .

∞

Легко видеть, что ЧХ K(ω) = ∑h(k) e−iωk имеет период 2π. Учиты-

k =0

вая, что h(n)=0 при n<0 и переходя к линейной частоте ν=ω /2π, частот-

∞

ную характеристику можем записать: K f (ν) = ∑h(k) e−2πiνk . Получи-

k =−∞

ли, что ЧХ K f (ν) представляет собой частотный спектр дискретного

сигнала – импульсной характеристики h(n) для единичного интервала дискретизации ∆t=1, см. раздел 3.4 и формулу (3.8). В частотной области

частота сигнала Fmax = 21∆t (см. (3.6)) соответствует нормированной

частоте ν=1/2 (ω=π), а период ЧХ (спектра ИХ), в соответствии со свойством периодичности спектра дискретного сигнала (см. раздел 3.4) в частотной области будет единичным для Kf(ν) и равным 2π для K(ω).

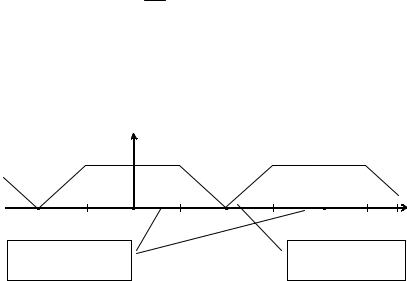
Фильтру низких частот, например, соответствует следующий схематический график для нормированной (по оси абсцисс) АЧХ │K(ω)│.

|K(ω)|

-π

2π

Низкиечастоты

Высокиечастоты

(полосапропускания)

(полосаподавления)

Пример 16.

Для

фильтра,

заданного

передаточной

функцией

H (z) =

+ cz −1 +

z −2 , c>0, найти АЧХ и ФЧХ, определить отклик y(n)

n −

в установившемся режиме на входное воздействие x(n) = sin

изобразить структурную схему фильтра.

◄

Для

передаточной

функции

получаем

выражение:

K(ω) = e

−iω

iω

+ c

−iω

= e

−iω

c(1 + cosω) . Для c>0

график АЧХ

K(ω) = c(1 + cosω)= 2c cos2 ω

приведен ниже. Представленный фильтр

является фильтром низких частот.

K(ω)

π/2

3π /2

2π

График ФЧХ

ϕ(ω) = −arg K(ω) = arg eiω

постройте самостоятельно,

помня, что по определению ϕ(ν) (−π;π]

(см. раздел 2.1).

В установившемся режиме отклик фильтра на гармоническое вход-

x(n) = Im ei

ное воздействие

3 n−

с циклической частотой ω=π /3 на-

ходим как

n−

π n

y(n) =

= −

cos

Im K

Структурную схему фильтра изобразите самостоятельно.

►

Глава 5.

Элементы прикладной теории информации

5.1. Дискретный источник сообщений без памяти, количество информации

Рассмотрим модель дискретного источника сообщений, который изменяет свое состояние в некоторые моменты

Состояние	x1	…	xN
Вероятность	p1	…	pN

времени, причём число возможных состояний конечно и равно N. Переходы источника X из одного состояния в другое случайны, не зависят от текущего и предыдущих состояний (говорят, что у источника сообщений «нет памяти»), а вероятности перехода в состояние xj (j=1,…,N)

p j = P{X = x j } заданы, ∑p j =1 . Если источник X находится в состоя-

j=1

нии xj, то с вероятностью pj в очередной момент наблюдения оно останется тем же, но при этом мы все равно говорим о переходе источника в новое состояние.

Состояние xj можно понимать как реализацию случайной величины дискретного типа, или как случайный выбор символа из некоторого N- символьного алфавита {x1,…,xN}. Последовательность символов на выходе источника представляет собой некоторое сообщение. Зададимся следующим вопросом: какую же информацию несёт в себе событие, состоящее в переходе источника X в новое состояние? Как измерить количество этой информации, приходящейся на один символ сообщения, т.е. как ввести меру для количества информации, создаваемой источником X при переходе в очередное состояние? Начнём рассуждения с частного случая дискретного источника сообщений, когда все состояния являются равновероятными, k=1,…,N: pk=1/N.

1. Дискретный источник с равновероятными состояниями

Естественно считать, что информация, которую несёт в себе один символ сообщения, т.е. один переход источника в новое состояние, тем больше, чем больше число состояний N. Например, если связать с символом сообщения результат вытягивания 1 карты из колоды в 32 карты, то при N=2 один символ может нести сообщение о цвете масти, а при N=32 – полную информацию о вытянутой карте. Таким образом, мера количества информации IX=IX(N) должна представлять собой монотонно

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1810 11 12 13 14 15 16 17 18 > Следующая >>>