
книжка умняшкина по моцос
.pdf
|
|
|
|
2 |
n |
2 ограничена свер- |
|||
Числовая последовательность sn = |
|
yn |
|
= ∑λ2j |
|
ϕ j |
|
||
|
|
|
|
|
j=1 |
|
|
|
|
ху, т.к. n sn = 
 x
x
 2 −
2 − 
 x − yn
x − yn 
 2 ≤
2 ≤ 
 x
x
 2 , и является неубывающей (sn+1≥sn). Поэтому {sn} – сходится. Сходимость последовательности частичных
2 , и является неубывающей (sn+1≥sn). Поэтому {sn} – сходится. Сходимость последовательности частичных
|
|
|
|
|
|
|
|
∞ |
|
|
2 , |
||
сумм {sn} означает, по определению, сходимость ряда |
s = ∑λ2j |
|
ϕ j |
|
|
||||||||
|
|
||||||||||||
причём |
|
|
|
|
|
j=1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
∞ |
2 ≤ |
|
|
|
2 . |
|
|
|
|
|
|
||
s = ∑λ2j |
|
ϕ j |
|
x |
|
|
|
|
(8) |
||||
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Неравенство (8) носит название неравенство Бесселя.
Определения. Ортогональная система {ϕk }∞k =1 H называется пол-
ной в гильбертовом пространстве H, если x H можем записать разложение:
∞ |
|
x = ∑λkϕk , |
(9) |
k =1 |
|
|
n |
т.е. lim x − ∑λkϕk = 0 . Ряд (9) называется рядом Фурье (по орто- |
|
n→∞ |
k =1 |
|
|
гональной системе {ϕk } ), а числа {λk } – коэффициентами Фурье.
Теорема 9. Пусть {ϕk }∞k =1 H – полная ортогональная система в гиль-
бертовом пространстве H. Тогда x H для |
коэффициентов Фурье |
{λk }k∞=1 верна формула (6). |
|
n |
|
◄ Обозначим частичную сумму xn = ∑λkϕk . |
В силу непрерывности |
k =1 |
|
скалярного произведения и ортогональности системы {ϕ }∞= имеем:
k k 1
|
|
|
|
n |
|
< x,ϕ j >= lim < xn |
,ϕ j >= lim |
∑λkϕk ,ϕ |
|
|
|
n→∞ |
n→∞ |
k =1 |
|
|
|
|
|
= lim |
∑n |
λk (<ϕk ,ϕ j >)= ∑∞ λk (<ϕk ,ϕ j |
>)= λj <ϕ |
|
n→∞ |
k =1 |
k =1 |
|
|
|
|
|||
j =
j ,ϕ j > ,
откуда следует формула (6). ►
21

Теорема 10. Ортогональная система {ϕk }∞k =1 H является полной в
гильбертовом пространстве H тогда и только тогда, когда x H неравенство (8) выполняется как равенство:
|
|
2 |
∞ |
2 , |
||
x |
|
= ∑λ2j |
|
ϕ j |
||
|
|
|
j=1 |
|
|
|
которое называется равенством Парсеваля-Стеклова.
◄ Действительно, понятие полной системы {ϕk }∞k =1 H означает, что
|
∞ |
|
|
|
∞ |
|
|
|
2 |
||||
|
|
|
|
|
|
||||||||
x H: |
x = ∑λkϕk |
и |
x − ∑λkϕk |
|
|
|
= 0 , |
||||||
|
k =1 |
|
|
|
k =1 |
|
|
|
|
||||
|
|
|
|
|
2 |
∞ |
|
|
2 = 0 , |
|
|
|
|
что эквивалентно равенству |
|
x |
|
− ∑λ2j |
|
ϕ j |
которое получается |
||||||
предельным переходом из (7). ► |
j=1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
Важнейшим примером гильбертова пространства является пространство функций L2[a,b] (см. пример 7). При этом под L2(R), или просто L2, будем понимать пространство всех функций, интегрируемых с квадратом на всей числовой оси (данное требование необходимо для
существования скалярного произведения < x, x >= 
 x
x
 2 ).
2 ).
1.7. Примеры ортогональных систем в пространстве L2
Элементами пространства в L2 являются функции. Приведём ряд примеров ортогональных функциональных базисов {ϕk}, которые нашли широкое применение на практике, в том числе, при обработке сигналов.
Пример 8. |
|
Тригонометрическая |
система |
функций |
||||
|
2π |
|
2π |
|
∞ |
|
|
|
1,cos |
|
kt,sin |
|
kt |
, как хорошо известно из курса специальных |
|||
T |
T |
|||||||
|
|
k =1 |
|
|
||||
разделов математического анализа, является полной системой на любом отрезке t [a,a+T] длины T.
22
Пример 9. Система многочленов Лежандра {Pk (t)}∞k =0 – ортогональна и
полна |
на отрезке |
t [-1,1]. |
P (t) =1, |
P (t) = t , |
P (t) = 1 |
(3t 2 |
−1) ,…, |
||||
|
|
|
|
|
|
0 |
1 |
2 |
2 |
|
|
|
|
|
|
((t 2 |
−1)n ),… |
|
|
|
|
|
|
Pn (t) = |
1 d n |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
2n n! dtn |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
При цифровой обработке сигналов использование степенных многочленов для представления сигналов часто более предпочтительно по сравнению с тригонометрическими функциями, так как вычисление последних реализуется обычно более сложным образом. В этой связи ещё более интересны базисы кусочно-постоянных функций.
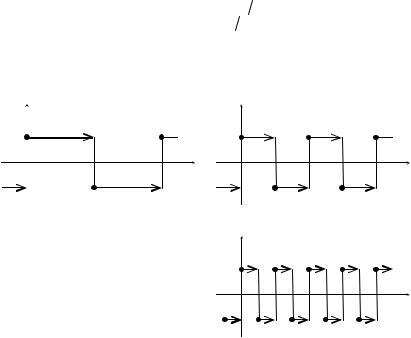
Пример 10. Систему функций Радемахера {rk (x)}∞k =0 определим сле-
дующим образом. Для x [0,1) положим |
||
r0 |
1 |
при x [0; 1 2) |
(x) = |
при x [1 2;1) |
|
|
−1 |
|
и периодически продолжим r0(x) на всю числовую ось с периодом T=1. Остальные функции системы определим так: rk (x) = r0 (2k x), k=1,2,…
(см. рис).
r0(x)
1
0 |
0,5 |
1 x |
-1
Для дальнейшего изложения удобно использовать следующее обо-
|
n m |
|
m +1 |
||||
значение: |
∆m = |
|
|
, |
|
n |
, где |
2 |
n |
2 |
|||||
|
|
|
|
|
|
||
n=0,1,…; m Z (целое число). Тогда из определения функций Радемахера и приведённых иллюстраций видны следующие свойства данной системы.
r1(x)
1
0 |
0,5 |
1 x |
-1
r2(x)
1
0 |
0,5 |
1 x |
-1
23
1°. Кусочное постоянство.
k +1 |
: |
rk ( x) |
|
1, еслиm - четное |
|
. |
|
|
|
|
|||||||||||
x ∆m |
= const = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
-1, еслиm - нечетное |
|
|
|
|
|
||||||||||
На более мелких подынтервалах, естественно, функции также по- |
|||||||||||||||||||||
стоянны: |
|
j ≥ k +1, x ∆j , m Ζ: |
|
|
|
|
|
|
|
|
|
||||||||||
k = 0,1,K, |
r (x) = const . |
(10) |
|||||||||||||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
k |
|
|
|
|
|
|
||
2°. Интеграл по периоду |
функции rk(x) |
равен нулю. Поэтому m |
|||||||||||||||||||
∫rk (x)dx = 0 (как интеграл по одному периоду, T = |
|
∆km |
|
= 2−k ) и |
|||||||||||||||||
|
|
||||||||||||||||||||
∆km |
m, j = 0,K,k : |
∫rk (x)dx = 0 , |
|
|
|
|
(11) |
||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
∆j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
как интеграл по N периодам, N = |
|
∆mj |
|
|
= |
2− j |
= |
2k − j . |
|
|
|||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
∆km |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2−k |
|
|
|
|
|
|
|||
3°. Система функций {rk (x)}k∞=0 |
– ортонормирована на отрезке x [0,1]. |
||||||||||||||||||||
◄ Очевидно, k |
rk , rk |
= ∫01(rk (x))2 dx =1 , т.е. функции нормирова- |
|||||||||||||||||||
ны. Покажем, что m ≠ k : |
rk , rm |
= ∫01rk (x)rm (x)dx = 0 . Пусть k≠m и |
|||||||||||||||||||
для определенности k>m, тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
∫ |
|
|
|
2k −1 |
∫ |
|
|
|
|
123 |
|
|
|
|
|
|
||
rk , rm = |
rk |
( x)rm |
(x)dx = ∑ |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
rk (x) rm ( x) dx = |
|
|
|||||||||||||||||
|
|
|
∆00 |
|
|
|
j=0 ∆kj |
|
|
|
|
c(m,k, j) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
см.(10) |
|
|
|
|
|
|
|
|
|
|
2k −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
∑c1(42m,k43, j) ∫rk (x)dx = 0 . |
|
|
|
|
|
|
► |
|||||||||||
|
|
|
j=0 |
±1 |
∆kj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14243 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
=0, см.(11) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, система функций {rk (x)}k∞=0 |
является ортонормирован- |
||||||||||||||||||||
ной, но не является полной в пространстве L2[0,1], поэтому в L2[0,1] сис- |
|||||||||||||||||||||
тема {rk (x)}k∞=0 |
не является базисом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Задание. Покажите самостоятельно по схеме, аналогичной доказательству свойства 3°, что ненулевой элемент f(x)=r0(x)r1(x), 
 f (x)
f (x)
 =1,
=1,
f(x) L2[0,1], является ортогональным любой из функций Радемахера, т.е. k: <f,rk>=0. Следовательно, система {rk (x)}∞k =0 не является базисом в L2[0,1].
Пример 11. Систему функций Уолша {wn ( x)}∞n=0 определим следующим образом. Представим целое число n≥0 в виде двоичного разложе-
l(n) |
|
|
|
|
|
|
ния: n = ∑nk 2k , nk {0,1}. Тогда функции системы Уолша выражаются |
||||||
k =0 |
|
|
|
|
|
|
при помощи функций Радемахера как |
|
|
|
|
|
|
l(n) |
= ∏rk (x) , |
|
|
|||
wn (x) = ∏(rk (x))nk |
|
(12) |
||||
k =0 |
|
k: nk =1 |
|
|
|
|
так как k (rk (x))0 =1 . Т.е. функция |
|
|
|
|
|
|
|
n |
n2 |
n1 |
n0 |
wn(x) |
|
Уолша wn(x) определяется как произ- |
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
w0(x)=1 |
|
ведение функций Радемахера с но- |
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
w1(x)=r0(x) |
|
мерами, которые соответствуют еди- |
|
|
|
|
|
|
|
2 |
0 |
1 |
0 |
w2(x)=r1(x) |
|
ничным индексам в двоичном раз- |
|
|
|
|
|
|
|
3 |
0 |
1 |
1 |
w3(x)=r0(x)r1(x) |
|
ложении числа n. При этом если все |
|
|
|
|
|
|
|
4 |
1 |
0 |
0 |
w4(x)=r2(x) |
|
коэффициенты {n } двоичного раз- |
|
|||||
k |
|
|
|
|
|
|
ложения равны нулю, то считаем последнее произведение в (12) равным единице, т.е. w0(x)=1. Поясним определение системы {wn (x)}∞n=0 построением её первых функций, см. табл.
Замечание. Очевидно, что функции системы Уолша имеют период T=1.
Задание. Постройте самостоятельно по определению (12) функции w3(x),…,w7(x) и их графики.
Теорема 11. На отрезке x [0,1] система Уолша ортонормированна.
◄ Очевидно, что n: <wn,wn>=1. Пусть теперь k≠n:
1 |
|
|
wk , wn = ∫ ∏rj (x) |
∏rj (x) |
dx = |
0 j:k j =1 |
j:n j =1 |
|
25

1 |
∏(rj ( x))2 |
|
|
|
1 |
|
= ∫ |
|
∏rj (x) dx = ∫ |
∏rj ( x)dx . |
|||
0 j:k j =n j =1 |
j:n j ≠k j |
|
0 |
j:n j ≠k j |
||
В подынтегральном произведении имеется по крайней мере один сомножитель, поскольку n≠k, и потому не все коэффициенты nj, kj одина-
ковы. Положим |
~ |
= max j |
и продолжим преобразования. |
||||
j |
|||||||
|
|
n j ≠k j |
|
|
|
|
|
|
|
|
|
|
|
константа |
|
|
1 |
|
|
~ |
|
c(k,n,m), ñì.(10) |
|
|
|
|
j |
|
64748 |
||
wk , wn = ∫r~j |
( x) ∏rj (x)dx = 2∑−1 ∫ r~j ( x) |
∏rj ( x) dx = |
|||||
|
0 |
j:n ≠k |
|
m=0 |
~ |
j:n ≠k |
|
|
j |
j |
j |
||||
|
j ~ |
|
∆m |
j ~ |
|||
|
|
j< j |
|
|
|
j< j |
|
~
2 j −1
∑c(k, n, m)
14243
m=0 ±1
∫rj (x)dx = 0 . |
► |
~ |
|
~ |
|
∆mj |
|
14243 |
|
=0, ñì.(11) |
|
Теорема 12. Система Уолша (12) - полная в пространстве L2[0,1]. ◄ Примем утверждение теоремы без доказательства. ►
Так как функции системы Уолша принимают лишь два значения
±1, они очень удобны для программных вычислений и для аппаратной реализации в цифровой аппаратуре.
Пример 12. Систему функций Хаара {hn (x)}∞n=0 определим на полуинтервале x [0,1) следующим образом. Положим h0(x)=1. Для n>0 номер базисной функции hn(x) представим следующим образом: n = 2k + m ,
где целые числа k≥0, 0≤m≤2k-1 однозначно определяются по номеру n>0. Тогда
|
|
2k 2 |
при x ∆k2+m1 |
|
|
|
||
hn (x) = |
|
|
k 2 |
k +1 |
|
. |
(13) |
|
− 2 |
|
при x ∆ |
2m+1 |
|
||||
|
|
0 |
при x ∆k |
= ∆k +1 |
∆k +1 |
|
|
|
|
|
|
|
m |
2m |
2m+1 |
|
|
|
|
|
|
|
|
h1(x) |
|
|
Приведём графики первых функций |
1 |
|
|
|||||
системы {hn (x)}n∞=0 . |
|
|
|
0 |
0,5 |
1 x |
||
26

h2(x) |
|
|
h3(x) |
|
|
2 |
|
|
2 |
|
|
0 |
0,5 |
1 x |
0 |
0,5 |
1 x |
h4(x) |
|
|
h5(x) |
|
2 |
|
|
2 |
|
0 |
0,25 |
1 x |
0 0,25 0,5 |
1 x |
Рассмотренным ранее свойствам системы Радемахера во многом аналогичны следующие очевидные свойства системы Хаара. Для n>0, n = 2k + m , k≥0, 0≤m≤2k-1:
1°. j ≥ k +1, l {0,1,K,2 j −1}, x ∆lj : hn (x) = const {0,−2k 2 ,2k 2 }.
2°. j {0,K, k} l {0,1,K,2 j −1} : ∫hn (x)dx = 0 .
∆lj
На основании данных свойств и определения (13) можно доказать, что система Хаара является ортонормированной.
Теорема 13. Система Хаара (13) является полной в пространстве L2[0,1]. ◄ Примем утверждение теоремы без доказательства. ►
27

Глава 2. Спектральное представление функций
Широкий класс устройств в электротехнике и радиоэлектронике описывается математической моделью линейной инвариантной во времени (ЛИВ) системы, преобразующей входной сигнал – функцию времени x(t) – в выходной сигнал y(t)=L{x(t)} по правилу, определяемому
+∞
формулой интегральной свёртки: y(t) = ∫x(τ)h(t −τ)dτ , где h(τ) – им-
−∞
пульсная характеристика системы. Легко можно показать, что для таких ЛИВ-систем функции вида eiωt являются собственными, т.е. L{eiωt } = Aeiωt , где А – некоторое комплексное число. Это означает, что
гармонические колебания не изменяют своей формы при прохождении через ЛИВ-систему, измениться может лишь их амплитуда и фаза. По этой причине базис гармонических колебаний наиболее удобен для анализа ЛИВ-систем, а спектральное (или частотное) представление функций при помощи преобразования Фурье является исключительно важным математическим аппаратом, используемым для анализа и синтеза систем обработки сигналов.
2.1. Тригонометрические ряды Фурье. Интеграл Фурье
Напомним следующую теорему.
Теорема 1. Если функция f(t) имеет период T и является кусочногладкой на периоде, то её ряд Фурье1 сходится к f(t) в каждой её точке
непрерывности и к значению |
|
1 |
( f |
( t + 0 ) + |
f ( t |
− 0 ) ) |
в точке |
|||||||||
2 |
||||||||||||||||
разрыва, то есть |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|||
|
f (t +0) + f (t − |
0) |
|
a |
0 |
|
|
2πk |
|
2πk |
|
|
||||
|
|
|
= |
|
+ ∑ ak cos |
|
t +bk sin |
|
|
t , |
(1) |
|||||
2 |
|
2 |
T |
T |
||||||||||||
|
|
k =1 |
|
|
|
|
||||||||||
где коэффициенты Фурье находятся по формулам:
1 Если не говорится, какая система функций рассматривается в виде базиса для построения ряда Фурье (см. раздел 1.6), то традиционно подразумевается использование тригонометрической системы.
28

|
|
2 T / 2 |
2πk |
|
|
|
|
|||||
ak |
= |
|
|
|
f (t) cos |
|
|
t dt, |
k = 0,1,K |
|
|
|
T −T∫ |
|
T |
|
|||||||||
|
|
2 |
|
|
|
|
(2) |
|||||
|
|
2 T / 2 |
2πk |
|
|
. |
||||||
|
|
|
|
|
||||||||
b |
= |
|
∫ |
|
f (t) sin |
|
|
|
t dt, |
k = 1,2,K |
|
|
T |
|
|
T |
|
||||||||
k |
|
|
|
|
|
|
|
|||||
|
|
|
−T 2 |
|
|
|
|
|
|
|
|
|
Задание. Убедитесь, что формула (2) является частным случаем (1.6) для L2[-T/2; T/2] из примера 8 главы 1.
Часто, однако, более удобной является комплексная форма записи ряда Фурье (1):
|
f (t +0) + f (t −0) |
|
∞ |
2πk |
|
|
||||||
|
= |
∑ck ei |
|
t , |
|
|||||||
|
T |
(3) |
||||||||||
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
k =−∞ |
|
|
|
|||
|
1 T / 2 |
|
|
|
|
2πk |
|
|
|
|
||
ck = |
|
∫ |
f |
(t)exp |
−i |
|
|
t dt, |
k = 0,±1,±2,K |
(4) |
||
T |
T |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
−T 2 |
|
|
|
|
|
|
|
|
|
|
Реальные сигналы, чаще всего, представляют собой апериодические функции, искусственная периодизация которых, необходимая для корректного использования разложений (1) или (3), представляет собой неоднозначную процедуру, приводящую к искажению сигнала. Поступим
следующим образом. Обозначим νk = k / T , |
∆νk =νk +1 −νk |
=1/ T = ∆ν , |
|||||||||
тогда из (3), (4): |
|
|
|
|
|
|
|
|
|
|
|
∞ |
2πk |
|
∞ |
T / 2 |
|
|
|
|
|
||
c ei |
|
t = |
∑ |
|
∫ |
f (u) exp(−i2πν |
|
u)du ei2πνk t ∆ν |
|
. |
|
T |
k |
k |
|||||||||
∑ k |
|
|
|
|
|
|
|
||||
k =−∞ |
|
|
k =−∞ −T 2 |
|
|
|
|
|
|||
Далее непериодический сигнал представим как периодический с бесконечно большим периодом.
T→∞
Тогда если существует интеграл
|
|
|
+∞ |
f (u) exp(−i2πν |
|
u)du , |
S(ν |
k |
) = lim c T = |
∫ |
k |
||
|
T →∞ k |
|
|
|||
|
|
|
−∞ |
|
|
|
то при формальном переходе Т→∞ получим для ряда (3):
29

|
∞ |
2πk |
|
|
∞ |
+∞ |
lim |
∑ck ei |
|
t |
= lim |
∑S(νk )ei2πνk t ∆νk = |
∫S(ν) exp(2πiνt)dν , |
T |
||||||
T →∞ k =−∞ |
|
|
∆ν →0 k =−∞ |
−∞ |
||
в случае существования последнего интеграла, который понимается в
смысле главного значения по Коши:
+∞ |
|
+N |
∫S(ν) exp(2πiνt)dν = |
Nlim→∞ |
∫S(ν) exp(2πiνt)dν . |
−∞ |
|
−N |
Данный интеграл носит название интеграла Фурье. Условия, при которых функция допускает представление в виде интеграла Фурье, определяет следующая теорема.
Теорема 2. Если функция f(t) абсолютно интегрируема на всей числовой
+∞
оси, т.е. ∫ f (t) dt < ∞ , и кусочно-гладкая на любом конечном отрезке
−∞
t [a,b] (-∞;+∞), то она представима в виде интеграла Фурье:
|
+N |
+∞ |
|
|
f (t) = Nlim→∞ |
∫S(ν) exp(2πiνt)dν = ∫S(ν) e2πiνt dν , |
(5) |
||
|
−N |
−∞ |
|
|
(считаем, что в точках разрыва f (t) = |
f (t +0) + f (t −0) |
), где |
|
|
2 |
|
|||
|
|
|
|
|
|
+∞ |
|
|
|
|
S(ν) = ∫ f (t) e−2πiνt dt . |
|
(6) |
|
−∞
Интеграл (6) носит название частотного спектра, или спектральной плотности, или спектральной характеристики функции (сигнала) f(t). Прямое (6) и обратное (5) преобразования Фурье записывают также с использованием в качестве аргумента (6) циклической частоты ω=2πν:
|
1 |
+∞ |
S(ω) = |
∫ f (t) e−iωt dt , |
|
|
2π |
−∞ |
f (t) = 1 |
+∞ |
|
∫S(ω) eiωt dω . |
||
|
2π |
−∞ |
Таким образом, при выполнении условий теоремы 2 сигнал можно однозначно описать как во временной области, т.е. через функцию времени f(t), так и в частотной области, через функцию частоты S(ν), оба
30
