
книжка умняшкина по моцос
.pdf
|
|
|
|
|
1 |
|
2πi |
|
N −1 |
|
|
|
|||
W = |
|
w |
|
|
− |
|
|
kj |
, |
а |
матрица |
ОДПФ |
|||
= |
N |
|
|||||||||||||
|
|
e |
|
|
|
||||||||||
|
k, j |
|
|
N |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
k, j=0 |
|
|
|
||
|
|
|
|
|
|
|
1 |
|
2πi |
N −1 |
|
|
|
||
W−1 = W |
= |
w |
= |
|
kj |
|
(убедитесь!). |
|
|||||||
e |
N |
|
|
||||||||||||
|
|
|
|
|
k, j |
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
k , j =0 |
|
|
|
Определение. Комплексная матрица W называется унитарной, если
W−1 = W* (сопряженная к W матрица, W* = WT ). Соответствующее дискретное преобразование B=WA также называется унитарным.
Как видим, ДПФ – унитарное преобразование. В частном случае,
для вещественных преобразований, W−1 = WT , и вместо понятия «унитарность» используется термин «ортогональность». Важнейшее свойство унитарных (ортогональных) преобразований – сохранение евклидовой нормы векторов – раскрывается в следующей лемме.
Лемма 1. Для любой унитарной матрицы W и любого вектора A евклидова норма вектора B=WA: 
 A
A
 E =
E = 
 B
B
 E .
E .
|
|
|
|
|
|
|
|
N −1 |
|
|
|
N −1 |
|
|
|
|||||||||||||||||||
◄ |
|
|
|
B |
|
|
|
2E = ∑ |
|
bk |
|
2 |
= ∑ |
|
|
|
T B = ( |
|
|
|
|
|
)T (WA)= |
|
||||||||||
|
WA |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
bk bk = |
B |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
k =0 |
|
|
|
k =0 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
T |
|
T WA = |
|
T A = |
|
|
|
A |
|
|
|
2 . |
► |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
A |
W |
A |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
123 |
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
E
Данное свойство сохранения евклидовой нормы преобразования B=WA представляет собой дискретный аналог равенства Парсеваля:
N∑−1 ak 2 = N∑−1 bk 2 .
k =0 |
k =0 |
3.6. Быстрое преобразование Фурье (БПФ)
Обозначим x(k)=xk, y(k)=yk и запишем ДПФ:
y(k) = 1 |
N −1 |
− |
2π i |
kj , |
|
∑x( j) e |
N |
(15) |
|||
N |
j =0 |
|
|
|
|
k = 0,K, N −1.
61
Хотя преобразование (15) определено для k=0,1,…,N-1, можно рассматривать (15) и для любого целого значения индекса k, при этом y(k)=y(k+N), т.е. период последовательности {yk }k Z равен размерности
ДПФ.
Рассмотрим ДПФ размерности N=2 |
n |
|
|
|
2πi |
|||
. Обозначив |
ωn = exp |
− |
|
, |
||||
|
||||||||
|
|
|
|
|
|
2n |
||
|
~ |
= N y(k) : |
|
|
|
|
||
запишем «ненормированное» ДПФ, y(k) |
|
|
|
|
||||
~ |
2n −1 |
kj |
|
|
|
(16) |
||
|
|
|
|
|||||
y(k) = |
∑x( j)ωn . |
|
|
|
||||
|
j =0 |
~ |
|
|
|
|
|
|
Для вычисления каждого коэффициента |
, как легко видеть, требу- |
|||||||
y(k) |
||||||||
ется около 2n комплексных сложений с умножениями. Итого, для реализации (16) требуется около 2n×2n=22n комплексных сложений с умножениями.
Пусть X0 = (x(0), x(2),K, x(2n −2))= (x0 (0), x0 (1),K, x0 (2n −1 −1)) – вектор чётных, а X1 = (x(1), x(3),K, x(2n −1))= (x1(0), x1(1),K, x1(2n −1 −1))
– |
нечётных отсчётов исходного вектора X. Тогда, замечая, что |
|
ω2 |
= ω |
, для (16) получаем (k=0,1,…,2n-1): |
n |
n−1 |
|
2n−1 −(1
~ = ∑
y(k) x(2
j=0
2n−1 −1 |
|
2n−1 −1 |
|
j)ωnk 2 j + x(2 j +1)ωnk(2 j+1) )= ∑x0 ( j)ωnkj−1 +ωnk ∑x1( j)ωnkj−1 , |
|||
j=0 |
|
j=0 |
|
1442443 |
1442443 |
||
~ |
(k) |
~ |
(k) |
Обозначимy0 |
Обозначимy1 |
||
где ~y0 (k) – k-й элемент ДПФ (16) размерности N=2n-1 вектора X0, а ~y1(k) – k-й элемент для ДПФ (16) вектора X1. Учитывая, что
~ |
~ |
|
n−1 |
|
~ |
|
|
~ |
|
|
n−1 |
|
|
2n−1 +k |
− |
2πi |
|
(k + 2 |
) , |
|
|
|
|
|
|
2n |
|||||||||
y0 |
(k) = y0 |
|
y1 |
(k) = y1(k + 2 |
|
) , и ωn |
= e |
|
|||||||||
последнее выражение для |
|
~ |
|
можем переписать: |
|
|
|||||||||||
|
y(k) |
|
|
||||||||||||||
|
|
|
|
|
|
|
~ |
|
~ |
(k) + |
k ~ |
(k) |
|
|
|||
|
|
|
|
|
|
y(k) |
= y0 |
ωn y1 |
|
|
|||||||
|
|
|
|
~ |
|
+ |
2 |
n−1 |
) |
~ |
(k) − |
k ~ |
(k) . |
|
|
||
|
|
|
|
y(k |
|
= y0 |
ωn y1 |
|
|
||||||||
|
|
|
|
|
|
|
|
k |
= 0,1,K,2n−1 −1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2n−1 +k )
= −ωnk ,
(17)
При |
|
помощи |
|
|
(17) |
мы |
выразили |
|
коэффициенты |
~ |
~ |
~ |
~ |
n |
−1)) ДПФ (16) размерности 2 |
n |
через коэффици- |
||
Y = (y(0), y(1),K, y(2 |
|
|
|||||||
62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n-1 |
~ |
~ |
~ |
~ |
|
n−1 |
−1)) и |
|
енты |
|
ДПФ |
размерности 2 : |
|
(2 |
|
||||||||
~ |
Y0 = (y0 |
(0), y0 |
(1),K, y0 |
|
||||||||||
~ |
|
~ |
~ |
n−1 |
|
|
|
|
|
|
|
|
||
= |
(y1(0), y1 |
(1),K, y1(2 |
−1)), которые получены из векторов X0 и X1 |
|||||||||||
Y1 |
|
|||||||||||||
соответственно.
Таким образом, вычисление 2n-точечного (для 2n отсчётов) ДПФ можно осуществить, выполнив предварительно два 2n-1-точечных ДПФ.
Вычисление спектров |
~ |
и |
~ |
размерности 2 |
n-1 |
по (16) требует около |
Y0 |
Y1 |
|
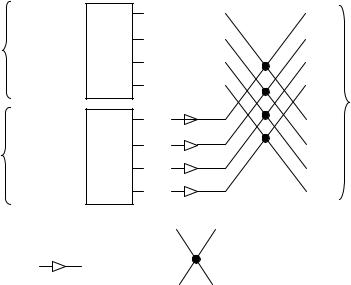
22(n-1) комплексных умножений в каждом случае, всего 22n-1 комплексных умножений. Ещё 2n-1 умножений требуется выполнить далее при дальнейшей реализации (17). Итого, реализация ДПФ (16) размерности 2n с использованием (17) потребует порядка 22n-1+2n-1~22n-1 операций комплексного умножения, т.е. примерно в два раза меньше, чем при непосредственной реализации ДПФ по формуле (16). Граф вычислений 8- точечного ДПФ по описанной схеме приведён на рисунке 3.4.
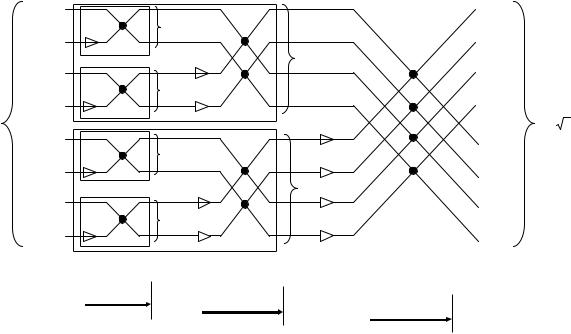
Дальнейшее использование идеи формулы (17) для ДПФ размерности N=8 дает полный граф вычислений, который изображен на рис. 3.5.
x(0)=x0(0)  x(2)=x0(1)
x(2)=x0(1)  4-точ.
4-точ.
X0 x(4)=x0(2)  ДПФ x(6)=x0(3)
ДПФ x(6)=x0(3) 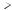
x(1)=x1(0) 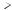 x(3)=x1(1)
x(3)=x1(1)  4-точ.
4-точ.
X1 x(5)=x1(2) 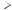 ДПФ x(7)=x1(3)
ДПФ x(7)=x1(3) 
Условные обозначения: a с ca
умножение
y0 (0) |
|
|
|
y(0) |
||||
~ |
|
|
|
|
~ |
|
|
|
~ |
|
|
|
|
~ |
|
|
|
y0 |
(1) |
|
|
|
y(1) |
|||
|
|
|
||||||
~ |
|
|
|
|
~ |
|
|
|
y0 |
(2) |
|
|
|
y(2) |
|||
|
|
|
||||||
~ |
|
|
|
|
~y(3) |
|||
y0 |
(3) |
|
|
|
||||
ω30 =1 |
||||||||
~ |
(0) |
~ |
(4) |
|||||
y1 |
ω3 |
y |
||||||
~ |
(1) |
~ |
(5) |
|||||
y1 |
ω32 |
y |
||||||
~ |
(2) |
~y(6) |
||||||
y1 |
ω33 |
|||||||
~ |
(3) |
~y(7) |
||||||
y1 |
|
|
|
|||||
|
a |
|
a+b |
|
|
|
||
|
|
|
|
|||||
|
|
|
Сложение-вычитание |
|
||||
|
|
|
|
|
|
|
||
|
b |
|
a-b |
|
|
|
||
~
Y
Рисунок 3.4. Граф вычислений ДПФ, определяемый формулой (17), на примере преобразования размерности N=8
63
x(0) x(4)
x(2)
x(6)
X
x(1)
x(5)
x(3)
x(7)
4-точечное ДПФ
ω10
2-точ. ДПФ
ω10
ω10
2-точ. ДПФ
ω10
~
Y0,0
~
Y0,1
~
Y1,0
~
Y1,1
ω20
ω2
ω20
ω2
|
4-точечное ДПФ |
Шаг 1 |
Шаг 2 |
|
~
Y0
ω30
ω3
~
Y1 ω32
ω33
~y(0)
~y(1)
~y(2)
~y(3)
~ =
Y 8Y
~y(4)
~y(5)
~y(6)
~y(7)
Шаг 3
Рисунок 3.5. Граф быстрого вычисления 8-точечного ДПФ (обозначения см. рис.3.4.)
64

В общем случае при размерности преобразования N=2n процедура сведения ДПФ к двум ДПФ меньшей размерности выполняется n раз. В соответствующем алгоритме быстрого преобразования Фурье (БПФ) имеем n шагов (см. также рис. 3.5). На j-м шаге 2n-j раз выполняются вычисления, аналогичные (17), результатом которых являются 2n-j «частичных» ДПФ размерности 2j, выполненные над некоторыми подмножествами отсчётов исходного вектора X. Каждый шаг требует (см. (17)) око-
ло N 2 = 2n−1 комплексных умножений (по сравнению с комплексными
2 = 2n−1 комплексных умножений (по сравнению с комплексными
сложениями или вычитаниями это намного более сложные арифметические операции, и именно по ним мы будем оценивать сложность алго-
ритма), итого в алгоритме БПФ имеем около n2n−1 комплексных умножений, вместо 22n при непосредственной реализации ДПФ по формуле (16). Так, для размерности N=210=1024 выигрыш в сокращении числа вычислительных операций – два порядка (около 200 раз).
Как видно из формулы (17) и примеров, приведённых на рис. 3.4 и 3.5, базовой операцией БПФ на j-ом шаге является так называемая «бабочка», см. рис. 3.6.
a |
|
a +bωkj |
j=1,…,n (номер шага) |
|
ωkj |
|
k=0,…,2j-1-1 |
|
|
||
|
a −bωkj |
||
b |
Рисунок 3.6. Элементарные операции алгоритма БПФ на j-м шаге
Алгоритм БПФ, основанный на рекуррентном использовании формулы (17), называется алгоритмом БПФ с прореживанием во времени, так как (см. также пример рис. 3.4) вычисление ДПФ размерности N сводится к обработке векторов X0, X1, полученных «прореживанием» (выбором каждого второго отсчёта, только чётных или только нечётных номеров) вектора X.
Запишем ДПФ и ОДПФ в матричном виде, исключив нормировочный множитель 1  N из структуры матриц преобразований:
N из структуры матриц преобразований:
Y = |
1 |
WX |
|
|
N |
|
|
||
|
|
, |
(18) |
|
|
1 |
|
||
X = |
|
|
|
|
|
|
|
||
N |
WY |
|
||
|
|
|
|
|
|
|
|
|
65 |

|
|
|
|
2πi |
N −1 |
|
|
где |
W = wl,m = exp |
− |
|
lm |
. Тогда алгоритм БПФ можно трак- |
||
N |
|||||||
|
|
|
|
l,m=0 |
|
||
товать как представление матрицы ДПФ в (18) в виде произведения слабозаполненных (т.е. состоящих в основном из нулевых элементов) матриц: W = WnWn−1 K W1 , где каждая матрица Wj соответствует j-му
шагу алгоритма БПФ
= ~ =
N Y Y Wn Wn−1 K W1X
{
142шаг431
14424L43
14442шаг4n−41 43
шаг n
и содержит в каждой строке лишь два ненулевых элемента: 1 и ωkj ,
k=0,…,2j-1-1. Представление матрицы ДПФ в виде произведения слабозаполненных матриц называют факторизацией матрицы.
Пример 4. Представить матрицу ДПФ размерности N=8 в факторизованном виде, соответствующем алгоритму БПФ с прореживанием по времени.
◄ Для N=23 получаем три матрицы-сомножителя в разложении метрицы
ДПФ: Y = 1 W3W2W1 X и, соответственно, три шага алгоритма БПФ
18442443
W
(см. рис. 3.5). Структура матрицы W3 соответствует последнему шагу алгоритма БПФ (изображенному на рис. 3.1) в использованных выше
~ |
Y~ |
|
~ |
~ |
~ |
есть со- |
обозначениях: Y = W |
0 |
|
, где Y = |
8Y , а векторы Y |
и Y |
|
3 |
Y~ |
|
|
0 |
1 |
|
|
1 |
|
|
|
|
|
ответственно результаты 4-точечных «ненормированных» ДПФ (16), выполненных над чётными X0 и нечетными X1 отсчётами вектора X. Несложно убедиться, что граф рисунка 3.4 (см. также (17)) соответствует следующей матричной операции умножения:
66
|
|
|
|
|
|
~ |
|
|
|
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
~ |
|
|
|
|
|
|
|
|
|
(0) |
|
|
0 |
1 |
0 |
0 |
0 |
ω |
0 |
0 |
|
(0) |
|
||||
|
|
|
|
|
y0 |
|
|
y0 |
|||||||||||||||
|
|
|
|
|
|
~ |
(1) |
|
|
|
|
|
|
|
3 |
2 |
|
|
|
~ |
(1) |
|
|
|
|
|
|
|
|
y |
|
|
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
y |
|
||||
|
|
|
|
|
~0 |
(2) |
|
ω3 |
~0 |
(2) |
|||||||||||||
|
|
~ |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
y |
|
||
~ |
|
|
|
~0 |
(3) |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
ω |
~0 |
(3) |
|||||||
Y |
= W |
|
y |
|
= |
|
|
|
y |
, |
|||||||||||||
Y = W |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
3 |
0 |
|
|||||||
3 |
|
~ |
|
3 |
|
~ |
(0) |
|
|
1 |
0 |
0 |
0 |
−1 |
0 |
0 |
0 |
|
~ |
(0) |
|
||
|
|
Y |
|
|
|
y1 |
|
|
|
|
y1 |
|
|||||||||||
|
1 |
|
~ |
(1) |
|
0 |
1 |
0 |
0 |
0 |
−ω |
0 |
0 |
~ |
(1) |
||||||||
|
|
|
|
|
|
y |
|
|
|
|
y |
|
|||||||||||
|
|
|
|
|
~1 |
(2) |
|
|
|
|
|
|
3 |
2 |
|
|
~1 |
(2) |
|||||
|
|
|
|
|
|
y |
|
|
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
y |
|
||||
|
|
|
|
|
~1 |
(3) |
|
−ω3 |
~1 |
(3) |
|||||||||||||
|
|
|
|
|
y1 |
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
−ω |
y1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
144444444424444444443 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W3 |
|
|
|
|
|
|
|
|
|
|
|
|
−i |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
где ω3 = exp |
4 |
. В свою очередь (см. рис. 3.5 и (17)) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
(0) |
|
|
1 |
0 |
1 |
0 |
|
~ |
|
|
|
1 |
0 |
1 |
0 |
|
y0 |
|
|
|
|||||||||||||||
~ |
~ |
(1) |
|
|
|
0 |
1 |
0 |
ω |
Y |
|
0 |
1 |
0 |
ω |
|||
Y0 = |
y |
|
= |
|
|
|
|
2 |
|
~ |
0,0 |
|
= |
|
|
|
2 |
|
~0 |
(2) |
|
1 |
0 |
−1 |
|
1 |
0 |
−1 |
|||||||||
|
y0 |
|
|
|
0 |
Y |
|
|
0 |
|||||||||
~ |
(3) |
|
0 |
1 |
0 |
|
|
|
0,1 |
|
0 |
1 |
0 |
−ω2 |
||||
y0 |
|
|
|
−ω2 |
|
|
|
|
||||||||||
~ |
(0) |
|
|
y0,0 |
|
||
~ |
(1) |
|
|
y |
|
, |
|
~0,0 |
(0) |
||
y0,1 |
|
|
|
~ |
(1) |
|
|
y0,1 |
|
|
|
~ |
(0) |
|
1 |
0 |
1 |
0 |
|
~ |
|
|
1 |
|
~ |
y1 |
|
|||||||||||
~ |
(1) |
|
|
0 |
1 |
0 |
ω |
Y |
|
0 |
|||
Y1 |
y |
|
= |
|
|
|
2 |
|
1,0 |
|
= |
|
|
= ~1 |
(2) |
1 |
0 |
−1 |
~ |
1 |
|||||||
|
y1 |
|
|
0 |
Y |
|
|
||||||
|
~ |
(3) |
0 |
1 |
0 |
|
|
1,1 |
|
0 |
|||
|
y1 |
|
|
−ω2 |
|
|
|
||||||
0 |
1 |
0 |
1 |
0 |
ω2 |
0 |
−1 |
0 |
1 |
0 |
−ω2 |
~ |
(0) |
|
|
y1,0 |
|
||
~ |
(1) |
|
|
y |
|
, |
|
~1,0 |
(0) |
||
y1,1 |
|
|
|
~ |
(1) |
|
|
y1,1 |
|
|
|
|
−i |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где ω2 = exp |
2 |
= −i . Отсюда для матрицы W2 получаем структуру: |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
~ |
|
(0) |
|
|
|
|
|
|
|
|
(0) |
|
y |
|
|
|||||||||||||||
|
|
|
|
y0 |
|
|
0 |
1 |
0 |
−i |
0 |
0 |
0 |
0 |
|
~0,0 |
(1) |
|
|
|||||
|
|
|
|
|
~y0 |
(1) |
|
|
|
y0,0 |
|
|
||||||||||||
|
|
|
|
|
~ |
(2) |
|
|
1 |
0 |
−1 0 |
0 |
0 |
0 |
0 |
|
|
~ |
|
(0) |
|
|
||
|
~ |
|
|
|
y0 |
|
|
y0,1 |
|
|||||||||||||||
|
|
|
~ |
(3) |
|
0 |
1 |
0 |
i |
0 |
0 |
0 |
0 |
|
|
~ |
|
(1) |
|
|
||||
Y |
= |
y |
|
= |
y0,1 |
. |
||||||||||||||||||
|
~0 |
|
~0 |
(0) |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
|
~ |
|
(0) |
|
|||||
|
Y |
|
|
|
y1 |
|
|
y1,0 |
|
|
||||||||||||||
1 |
|
~ |
(1) |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
− i |
|
|
~ |
|
(1) |
|
|
||||
|
|
|
|
y1 |
|
|
|
|
y1,0 |
|
|
|||||||||||||
|
|
|
|
|
~ |
(2) |
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
||
|
|
|
|
|
y |
|
|
0 |
0 |
0 |
0 |
1 |
0 |
−1 0 |
|
(0) |
|
|||||||
|
|
|
|
~1 |
(3) |
|
|
y1,1 |
|
|
||||||||||||||
|
|
|
|
y1 |
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
i |
|
~ |
(1) |
|
|||||
|
|
|
|
|
|
|
|
|
|
y1,1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1444442444443 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
W2 |
|
|
|
|
|
|
|
|
|
|
|
67

Аналогично, по графу рисунка 3.5 получаем структуру матрицы W1:
~ |
|
(0) |
|
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
y |
|
|
|
|
|
|
||||||||||||
~0,0 |
(1) |
|
|
|
1 |
0 |
0 |
−1 |
0 |
0 |
0 |
0 |
x(0) |
|
||||
y |
|
|
|
|
|
|
x(1) |
|
|
|||||||||
~0,0 |
(0) |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
|
|
|||||
y0,1 |
|
|
|
x(2) |
|
|
||||||||||||
~ |
|
(1) |
|
|
0 |
0 |
1 |
0 |
0 |
−1 |
0 |
0 |
|
|
x(3) |
|
|
|
y0,1 |
= |
|
. |
► |
||||||||||||||
~ |
|
(0) |
|
|
|
|
|
|
|
|
|
|
|
x(4) |
||||
y |
|
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
|
|
|||||
~1,0 |
|
(1) |
|
|
|
|
x(5) |
|
||||||||||
y |
|
|
0 |
1 |
0 |
0 |
−1 0 |
0 |
0 |
|
|
|
||||||
~1,0 |
(0) |
|
|
x(6) |
|
|||||||||||||
y |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
|
|
||||||
1,1 |
|
|
|
|
|
|
||||||||||||
~ |
(1) |
|
|
0 0 0 1 0 0 0 |
|
x(7) |
|
|
||||||||||
y1,1 |
|
|
|
−1 |
|
|
|
|
||||||||||
|
|
|
|
|
1444442444443 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
W1 |
|
|
|
|
|
|
|
|
|
Кратко остановимся на построении быстрого алгоритма обратного ДПФ. Все проведённые рассуждения для прямого ДПФ (16) можно в
|
|
2πi |
|
|
2πi |
|||
точности повторить, вместо ωj = exp |
− |
|
|
положив |
ωj = exp |
|
, |
|
2 j |
2 j |
|||||||
|
|
|
|
|
|
|||
верными останутся и аналитическое выражение (17), и примеры графов вычислений, приведённые на рисунках. Однако имея вычислительную
~ =
процедуру реализации ДПФ Y WX , т.е. реализацию умножения мат-
рицы ДПФ на вектор: V=WU, умножение на матрицу W , необходимое при ОДПФ (см. (18)), можно выполнить в три этапа. Реализация процедуры B = WA сводится к следующей последовательности действий.
1.U← A . (Сформировать вектор U из комплексно сопряженных компонент вектора A.)
2.V=WU. (Используя имеющуюся процедуру реализации ДПФ, выполнить умножение матрицы на вектор.)
3.B ← V . (Сформировать вектор B из комплексно
сопряженных компонент вектора V.)
Таким образом, реализовав быстрый алгоритм умножения на матрицу W, сразу получаем и процедуру быстрого алгоритма умножения на мат-
рицу W .
3.7. Дискретное преобразование Уолша
Определение. Дискретным преобразованием Уолша (ДПУ) вектора X = (x0 , x1,K, x2n −1 ) назовем вектор Y = (y0 , y1,K, y2n −1 ), компоненты которого находятся по формуле:
68
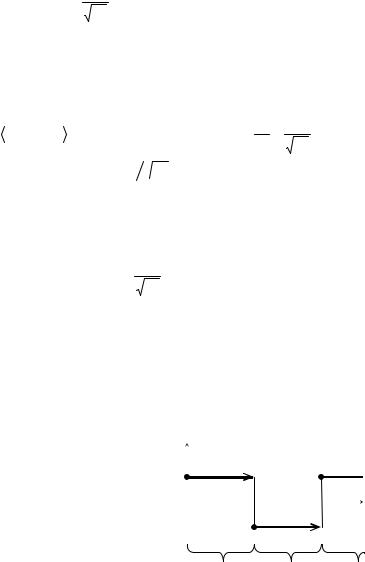
yk = 1 |
2n −1 |
|
∑x j wk ( j / 2n ) , |
(19) |
|
2n j=0 |
|
|
где wk(t) – k-я функция системы Уолша (см. раздел 1.7). |
|
|
Замечание. Положив, |
что xj – это отсчёты некоторой |
функции, |
xj=f(j/2n), определённой на отрезке t [0;1], формулу (19) можно рассматривать как приближённое вычисление по формуле прямоугольников интеграла:
1 |
n |
1n |
= 1 yk |
ck = f (t), wk (t) = ∫ f (t)wk (t)dt ≈ |
2∑−1 x j wk ( j / 2n ) |
||
0 |
j =0 |
2 |
2n |
(с точностью до множителя 1  2n ). Напомним, что ck представляет
2n ). Напомним, что ck представляет
собой k-й коэффициент Фурье разложения функции f(t) по системе Уолша.
ДПУ часто удобнее представлять в матричном виде, Y=WX, где
|
|
|
= 1 |
|
|
2n −1 |
матрица ДПУ W = |
|
w |
|
w ( j / 2n ) |
. |
|
|
|
k, j |
|
n |
k |
|
|
|
{ |
2 |
14243 |
|
|
|
эл-т матрицы |
|
|
отсчётф.Уолша k , j =0 |
||
Лемма 2. Матрица ДПУ – симметрическая, т.е. W=WT.
◄ Напомним, что любое вещественное неотрицательное число t R
можно |
записать |
в |
виде |
двоичного |
разложения: |
∞ |
M (t) |
|
−1 |
|
|
t = ∑tm 2m = ∑ tm 2m |
+ |
∑tm 2m |
, где m |
tm {0,1} и |
|
m=−∞ |
m=0 |
|
m=−∞ |
|
|
|
14243 |
|
14243 |
|
|
[ x] - целая часть {x}− дробная часть
tm ≡ [t / 2m ] (mod 2) , 0≤tm≤1. Тогда
для t≥0 функцию r0(t) системы Радемахера (определение системы см. раздел 1.7) можно определить следующим образом (убедитесь!):
r0 |
|
∞ |
m |
1, приt−1 =0 |
||
(t) =r0 |
∑tm 2 |
= −1, при t |
−1 |
=1. |
||
|
m=−∞ |
|
|
|
||
Напомним, что |
r |
(t) = r (2m t) , по- |
||||
|
|
|
m |
0 |
|
|
r0(t)
1
0 |
0,5 |
1 |
t |
-1
t-1=0 |
t-1=1 |
|
t-1=0 |
69

этому |
для |
точек |
t = j 2n |
можем |
записать: |
r ( j / 2n ) = r |
|
2m−n |
M ( j) |
|
|
∑ |
|||
m |
{ 0 |
|
|
|
|
t |
|
|
µ=0 |
jµ 2µ = r0 M∑( j)
µ=0
l |
|
M ( j)+m−n |
|
|
|
64748 |
|
||||
jµ 2µ+m−n |
= r0 |
∑ |
jl −m+n 2l |
. |
|
|
|
|
l =m−n |
123 |
|
|
|
|
tl |
|
|
Отсюда |
|
|
|
r |
( j / 2n ) = |
1, при j−1−m+n |
= 0 |
= (−1) jn−1−m . |
|
|
|
|
||||||||||
|
|
|
|
m |
|
|
|
−1, при j |
|
|
=1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
−1−m+n |
|
|
|
|
|
|
|
|
|
||
Поэтому для функций Уолша при k=0,…,2n-1 имеем: |
|
|
|
|
|
|||||||||||||||||
j |
|
n |
−1 |
j |
km |
n |
−1 |
|
|
j n−1−m km |
|
n−1 |
kn−1−µ jµ |
|
k |
|
||||||
wk |
|
|
|
= ∏ rm |
|
= |
∏(-1) |
µ |
= ∏(-1) |
= wj |
|
, |
||||||||||
|
n |
n |
n |
|||||||||||||||||||
2 m=0 2 |
|
|
|
|
123 |
|
|
|
|
|
2 |
|||||||||||
m=0 |
|
|
|
|
|
µ=0 |
|
|
||||||||||||||
т.е. w |
j |
= |
|
1 |
w |
( j / 2n ) = 1 |
|
w |
j |
(k / 2n ) = w |
j,k |
, и |
матрица |
ДПУ – |
||||||||
k, |
|
|
2n |
k |
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
симметрическая. ►
Теорема 4. Матрица ДПУ – ортогональна.
◄ Нужно доказать, что W-1= WT. Для этого обозначим U=WWT=WW и
покажем, что матрица U – единичная, т.е. |
1, приk = j |
. Рассмот- |
|
uk, j = |
j |
||
|
0, приk ≠ |
|
|
рим элемент k-ой строки j-ого столбца матрицы U, который представляет собой скалярное произведение k-ой строки матрицы W и j-ого столбца матрицы W:
|
2n −1 |
|
|
2n −1 |
2n −1 1 |
m |
m |
|
||||||||||||||||||
uk, j = |
∑wk,m wm, j = |
∑wk,m w j,m = |
∑ |
|
|
wk |
|
|
|
|
w j |
|
|
|
. |
|
||||||||||
|
n |
2 |
n |
|
|
n |
|
|||||||||||||||||||
|
m=0 |
|
|
m=0 |
|
m=0 2 |
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||
Поскольку k=0,…,n-1 rk(t)=const при |
|
|
n |
|
m |
m +1 |
|
|||||||||||||||||||
t ∆m = |
|
|
|
|
; |
|
|
|
(см. (1.10)), |
|||||||||||||||||
|
|
n |
2 |
n |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n−1 |
|
|
|
|
||
то на этих же интервалах ∆nm также ν<2n |
wν (t) = ∏(rk (t))νk = const . |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =0 |
|
|
|
|
||
Поэтому последнее выражение для uk,j можем переписать: |
|
|
|
|
||||||||||||||||||||||
n |
|
|
|
|
|
|
|
1 wk (t)wj (t)dt =<wk (t), wj (t)>= 1, приk = j |
|
|||||||||||||||||
uk, j = 2∑−1 |
∫ |
wk (t)wj (t) |
|
dt = |
, |
|||||||||||||||||||||
|
14243 |
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, приk ≠ j |
|
|||
m=0 ∆nm |
m |
m |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
const=w |
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 2n |
j 2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
в силу ортонормированности системы Уолша (см. теорему 1.11). ►
70
