книжка умняшкина по моцос

Следуя общей схеме объединения символов в пары, тройки и т.д., теоретически можно как угодно приближать величину битовых затрат на кодирование одного символа к значению двоичной энтропии, для самого общего случая источника сообщений с произвольными объемом (количеством символов) алфавита и распределением вероятностей. Однако на практике это не всегда целесообразно и технически возможно: например, если источник имеет 256 состояний, то при рассмотрении пар символов потребуется составлять таблицу кодов уже для 256×256=65536 символов, а снижение избыточности кодирования при этом может быть крайне незначительным. В любом случае, невозможно получить битовые затраты меньшие, чем теоретический предел, который определяется величиной двоичной энтропии источника.

Как отмечалось при рассмотрении примера 4, методика ШеннонаФано имеет некоторую неоднозначность, и в результате её применения могут получаться различные по эффективности коды. Этого недостатка лишен получивший значительно более широкое распространение метод построения эффективных кодов, предложенный Хаффманом. Коды Хаффмана нередко оказываются эффективнее кодов Шэннона-Фано.

Метод построения эффективных кодов по Хаффману.

1.Построение дерева Хаффмана.

1.1.Упорядочить таблицу символов в порядке убывания вероятностей: p1≥…≥pk≥….

1.2.Два последних символа, имеющих наименьшие вероятности появления, объединяем в один новый символ, которому приписываем суммарную вероятность объединенных символов. Если в полученном алфавите имеем более одного символа (вероятность которого равна 1), то переходим на шаг 1.1, иначе - на шаг 2.

Комментарий. Вершина полученного дерева Хаффмана – это единственный символ окончательного алфавита, листья – символы исходного алфавита, прочие узлы – символы промежуточных алфавитов, полученные в результате слияния других символов.

2.Построение битового кода. Из каждого узла дерева Хаффмана (за исключением листьев) выходят по два ребра; приписываем одному ребру бит «0», другому – «1». Код каждого символа исходного алфавита получается в результате последовательного дописывания битов, соответствующих ребрам графа, которые необходимо пройти от вершины дерева до листа-символа.

111

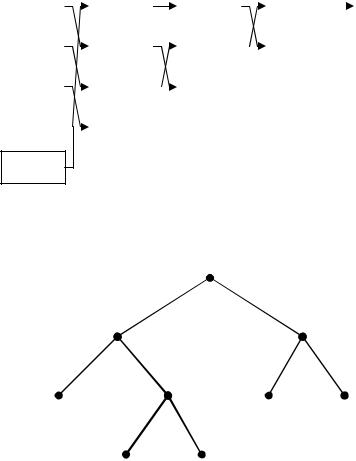
Пример 6. Построить по методике Хаффмана эффективный двоичный код для источника, имеющего 5 равновероятных состояний.

◄ Для определённости положим, что символами исходного алфавита являются буквы {A,B,C,D,E}. Процедуру построения дерева Хаффмана (шаг 1 алгоритма) тогда можно изобразить в виде следующей схемы.

E

p(E)=0.2 Построение соответствующего двоичного кода по дереву Хаффмана (выполнение шага 2 алгоритма) отражает следующий ниже рисунок. Двоичная энтропия источника сообщений в данном случае H=log25≈2,32 (бит), а полученные битовые

затраты R=2,4 бит (избыточность кода – около 3%).

p(A,B,C,D,E)=1

112

Задание. Постройте самостоятельно коды Хаффмана для источника сообщений, рассмотренного в примере 4. Убедитесь в том, что битовые затраты составят величину 2,80 бит на символ, т.е. соответствуют лучшему из рассмотренных в примере 4 вариантов построения кода Шеннона-Фано.

5.3. Условная энтропия

Вводя понятие энтропии (2) как меры априорной неопределенности состояния источника сообщений, мы требовали, чтобы для ансамбля независимых источников X и Y выполнялось условие H(XY)=H(X)+H(Y). Если же источники зависимы, то информация о реализации того или иного состояния одного источника позволяет уменьшить априорную неопределенность состояния другого; интуитивно понятно, что это должно означать следующее: H(XY)<H(X)+H(Y), и в общем случае

то есть, расписав данное выражение в соответствии с определением (2):

− ∑∑p(xi , y j )log p(xi , y j )≤ − ∑p(xi ) log p(xi )− ∑p( y j ) log p( y j ) ,

необозначенные границы суммирования означают здесь «по всем возможным значениям», т.е. пределы суммирования определяются способом нумерации и количеством возможных состояний источников сообщений. Справедливость неравенства (3) может быть доказана строго, но мы этого делать не будем.

Ансамбль двух источников сообщений можно описать, задав закон совместного распределения вероятностей всевозможных пар состояний (xi,yj), например, в виде таблицы распределения вероятностей {pi, j = P(X = xi ,Y = y j )}. Удобно трактовать пары (xi,yj) как реализации

случайного вектора (X,Y), компоненты которого являются случайными величинами дискретного типа. Дискретные случайные величины Х, Y являются независимыми, если i,j:

P(X = xi ,Y = y j )= P(X = xi )P(Y = y j ).

14424443 1424314243

pi, j = p( xi , y j ) p( xi ) p( y j )

В общем же случае, когда случайные величины зависимы, вероятность

Итак, если между источниками существует статистическая зависимость, то знание о реализации состояния одного источника может только уменьшить неопределенность другого.

Пример 7. Показать, что если состояния источника Y связаны жесткой (функциональной) зависимостью ϕ с состояниями источника X:

энтропия m H (Y xm ) = −∑p( yk xm ) log p( yk xm ) = 0 , и следовательно,

k

H (Y X ) = 0 . Отсюда, в силу (6): H ( X ,Y ) = H ( X ) . ►

Если приведённые рассуждения обобщить на ансамбль из n дискретных источников информации (X1,…,Xn), то для энтропии ансамбля можно получить следующее выражение:

H(X1, X2 ,K, Xn ) = H(X1) +H(X2 X1) +H(X3 X1X2 ) +K+H(Xn X1X2 KXn−1),

где

H ( X j X1X 2 KX j −1) = −∑K∑p(xk1 ,K, xk j−1 ) ×

k1 k j−1

×∑p(xk j xk1 ,K, xk j−1 ) log p(xk j xk1 ,K, xk j−1 ) .

1k j 4444444( 42444)444443

−H X j xk1 ,K, xk j−1

Причём вновь (не доказываем): H ( X j X1X 2 KX j−1) ≤ H ( X j ) . Поэтому

n

H(X1, X2 ,K, Xn ) ≤ ∑H(X j )

j=1

(равенство имеет место для ансамбля независимых источников).

безусловная энтропия H(U)=1 (бит). Энтропия ансамбля (U,V):

115

H(UV) =−∑∑pi, j log2 pi, j =−0,4log2 0,4−0,1log2 0,1−0,2log2 0,2−0,3log2 0,3≈1,85

5.4. Кодирование сообщений источника с памятью

Используя понятие условной энтропии, рассмотрим специфику алгоритмов эффективного кодирования данных, порожденных источниками сообщений «с памятью», для которых вероятности переходов в очередные состояния зависят от предыстории прошлых состояний. Другими словами, имеется вероятностная зависимость между очередным символом, создаваемым источником сообщения, и реализациями предыдущих символов (состояний). При этом мы вновь рассматриваем дискретный источник X, число состояний которого конечно и описывается некоторым алфавитом {x1,…,xN}.

В качестве модели источника будем рассматривать источник с конечной памятью. Это означает, что на распределение вероятностей для текущего перехода источника в очередное состояние оказывает влияние то, какие именно предшествующие состояния источника имели место, причём достаточно учитывать лишь конечное число M предыдущих состояний. То есть вероятности перехода источника в очередное состояние задаются условными законами распределения. Обозначая X(m) – m-ое состояние источника при априорном рассмотрении (нереализованное состояние), x(m) – при апостериорном рассмотрении (реализованное состояние), для описания вероятностей перехода источника с памятью необходимо знать, таким образом, условные распределения вероятностей:

k=1,…,N.

Для того чтобы полностью описать математическую модель источника с памятью, необходимо задать закон совместного распределения вероятностей, т.е. (M+1)-мерную таблицу

m0 , m1,K, mM {1,K, N} (очевидно, что количество элементов в этой

116

таблице NM+1). Тогда по совместному закону распределения (8) условный закон (7) может быть найден следующим образом:

Если известна конкретная реализация состояний (x(m-1),…,x(M-1)), то известен частный закон распределения вероятностей перехода в очередное состояние x(m) и неопределённость перехода можем оценить по частной условной энтропии (сравните с (4)):

k=1

При этом каждому набору M предшествующих состояний соответствует, вообще говоря, своя таблица условного распределения вероятностей (7), на которой основывается построение процедуры эффективного кодирования очередного символа (т.е. состояния) источника с битовыми затратами, минимальное значение которых оценивается по величине (9) (с двоичным основанием логарифма). Среднее количество информации, связанное с очередным переходом источника в новое состояние и выдачей очередного символа сообщения, тогда оценивается по условной энтропии (сравните с (5)):

Величина (10) является оценкой для минимальных битовых затрат, приходящихся в среднем на кодирование одного символа сообщения источника информации с памятью.

Как же реально организовать процедуру эффективного кодирования? Положим, что мы каким-то образом закодировали M символов сообщения, (т.е. эти символы известны). Тогда для кодирования очередного символа эффективный код необходимо строить (например, по Хаффману), исходя из таблицы условных распределений (7). Для осуществления кодирования, таким образом, таблицы эффективных кодов для N символов необходимо построить для каждой возможной реализации наборов предшествующих состояний, всего получаем NM таблиц по N эле-

117

ментов, т.е. массив данных из NM+1 ячеек. Например, если возможно 256 состояний источника (в алфавите источника сообщений 256 символов), то влияние одного единственного предшествующего состояния (M=1) на очередной переход источника в общем случае потребует создания таблиц кодов из 2562=65536 ячеек. Если не учитывать предшествующие состояния при кодировании очередного символа, то получаемые коды могут оказаться неэффективными, обладать значительной избыточностью, характеризуемой различием безусловной энтропии источника (2) и условной энтропии (10), для которых верно соотношение:

H ( X ) ≥ H (X (m) X (m −1),K, X (m − M )) (равенство имеет место для источника без памяти).

Пример 9. Пусть последовательность символов сообщения X(m) создается источником, для которого вероятности перехода в новое состояние зависят только от текущего состояния, а совместный закон распределения pm0 ,m1 = P(X (m) = xm0 , X (m −1) = xm1 ), задан следующей таблицей

◄ а) Если нет возможности учитывать предыдущее состояние источника, то эффективные коды строим по безусловному распределению вероятностей. Используя методику Шэннона-Фано или Хаффмана, получаем среднюю длину битового кода R=1,5 бит, что совпадает с безусловной двоичной энтропией источника.

б) Возможны три варианта выбора статистической модели условного распределения вероятностей для символа X(m) по реализации символа

X(m-1).

дующей таблицей вероятностей. Частная условная энтропия источника совпадает со средни-

ми битовыми затратами полученного кода:

H ( X (m) | X (m −1) = x1) = R( X (m) | X (m −1) = x0 ) =1,5 (бит).

118

тами полученного кода и равна 1 биту.

X(m-1)= x3. В этом случае очередное состояние источника полностью определено, кодирование состояния X(m)=x1 не требуется.

H ( X (m) | X (m −1) = x3 ) = H ( X (m) | X (m −1) = x3 ) = 0 (бит).

В данном примере при использовании информации о предыдущем состоянии источника получили минимально возможную среднюю длину битового кода одного символа, равную условной энтропии источника:

3

H ( X (m) | X (m −1)) = ∑P( X (m −1) = xk )H ( X (m) | X (m −1) = xk ) =

k =1

щей таблицей распределения вероятностей. Оценить минимальные битовые затраты R, которые необходимы для кодирования символов сообщения, если:

а) предыдущее состояние источника не учитывается, б) предыдущее состояние источника учитывается.

◄ Оцените битовые затраты, самостоятельно подсчитав величину безусловной и условной энтропии данного источника. ►

К сожалению, на практике учет межсимвольных зависимостей вероятностного характера часто упирается в упомянутую проблему размерности таблиц распределения вероятностей.

119

5.5. Неопределенность непрерывного источника сообщений. Дифференциальная энтропия

Рассмотрим возможность применения понятия энтропии к случайной величине непрерывного типа X (соответствующей непрерывному источнику информации), заданной функцией плотности вероятности f(x)

1

на интервале x [0,1), ∫ f (x)dx =1. Положим, что f(x) – непрерывна.

0

Равномерно разобьем интервал [0,1) на N участков ∆ j = [ju, (j +1)u) длины u=1/N, j=0,1,…,N-1. Случайной величине X, попавшей в интервал ∆j, поставим в соответствие значение x j = u(j + 12 ). Получаем из непрерывной величины X равномерно проквантованную с шагом u дискрет-

ˆ

ную случайную величину X , энтропия (2) которой, в соответствии с интегральной теоремой о среднем:

где θj - некоторая точка из интервала ∆j. При этом математическое ожи-

где ξj - некоторая точка из интервала ∆j.

120