книжка умняшкина по моцос

Добавил:

korayakov Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

Математическое обеспечение цифровой обработки и кодирование сигналов

Файл:

риоде ν 0;

по оси частоты отсчёты

s j = S (ν j ) в точках ν j =

.pdf

Скачиваний:

133

Добавлен:

16.04.2013

Размер:

1.55 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 186 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

2πFt

торой ϕk(k∆t)=1. То есть в представлении для f(t) в виде (5) получаем,
что в точках t=tm=m∆t в сумме (5) имеем единственное ненулевое сла-
гаемое.			y(t)
			y(t)
1
0.8
0.6
0.4
0.2
0					t
0
-0.2
-0.4	-2/F	-1/F -1/2F	0	1/2F 1/F	2/F
	-2/F	-1/F -1/2F	0	1/2F 1/F	2/F
Рисунок 3.1. Графики базисных функций ϕ0(t) (сплошная линия) и ϕ1(t) (пунк-
тирная линия) ряда Котельникова (5)

Покажем, что система функций	ϕ	k	(t) = sin(2πF(t − k∆t))		-
		k	2πF(t − k∆t)
			2πF(t − k∆t)	k Ζ

ортогональна на числовой оси t (-∞;∞).

Теорема 2. Для системы функций	ϕ	k	(t) = sin(2πF(t − k∆t))		,
		k	2πF(t − k∆t)
			2πF(t − k∆t)	k Ζ

	1		∞		1/ 2F		приk = m
∆t =			= ∫
		, верно: ϕk (t),ϕm (t)		ϕk (t)ϕm (t)dx =		0	приk ≠ m	.
	2F
			−∞

◄ Предварительно заметим, что спектр функции ϕ0 (t) =ϕ(t) = sin 2πFt :

1
		, приν [−F; F ] . Действительно, выполняя обратное пре-
	2F
Sϕ (ν) =
	0,	приν [−F; F ]

∞	1	F		sin 2πFt
образование Фурье, видим: ∫Sϕ (ν) e2πiνt dν =		∫e2πiνt dν	=		.
	2F
−∞		−F		2πFt

Теперь рассмотрим скалярное произведение

					∞		∞
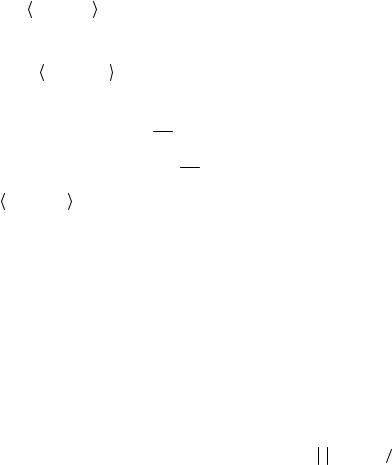
ϕ	k	(t),ϕ	m	(t) =	∫	ϕ(t −k∆t)ϕ(t −m∆t)dt =	∫	ϕ(x)ϕ(x −(m −k)∆t)dx
	k		m		∫	123	∫
					−∞	Обозн. x	−∞

и обозначим u=(m–k)∆t. В силу чётности функции ϕ(x-u)=ϕ(u-x), поэтому

+∞

g(u) = ϕk (t),ϕm (t) = ∫ϕ(x)ϕ(u − x)dx – свертка функций ϕ(t) и ϕ(t).

−∞

Тогда в соответствии со свойством 5° интеграла Фурье спектр функции g(u): Sg (ν) = Sϕ (ν)Sϕ (ν) = 21F Sϕ (ν) , и в силу линейности преобразова-

ния Фурье (свойство 2°) g(u) = 21F ϕ(u) . Поэтому

ϕk (t),ϕm (t) = g((m − k)∆t)=	1	ϕ((m − k)∆t)= 1/ 2F	приk = m				. ►
ϕk (t),ϕm (t) = g((m − k)∆t)=	2F	ϕ((m − k)∆t)= 1/ 2F	приk ≠ m				. ►
	2F	0	приk ≠ m
Таким образом, сдвиги ϕ(t) образуют функциональную систему, ко-
торая является ортогональным		базисом для представления функций,
				1		1
спектр которых ограничен частотной полосой ν −					;		. Коэф-
				2∆t		2∆t

фициенты Фурье ряда Котельникова (5), т.е. коэффициенты разложения по базису {ϕk}, находятся очень просто, равномерной выборкой отсчётов анализируемой функции: λk = f (k∆t) , k Z. По этому набору отсчётов

мы можем восстановить значение функции в любой точке числовой оси t (-∞;∞) - соответствующее правило восстановления определяет ряд (5), который можно рассматривать как интерполяционную формулу, имеющую при правильном выборе периода дискретизации нулевую ошибку интерполяции для функций с финитным спектром.

Итак, шаг дискретизации ∆t позволяет точно восстановить аналого-

вый сигнал, если спектр функции ограничен: max ν = Fmax ≤1 2∆t .

S (ν )≠0

Отсюда, окончательно, критерий для выбора шага дискретизации аналогового сигнала при известной максимальной («верхней») частоте Fmax спектрального представления принимает следующий вид:

∆t ≤	1	.	(6)

	2F
	max

Величину f Д =1∆t называют частотой дискретизации. В этих обозна-

чениях условие (6) можно переписать в эквивалентном виде:

f Д ≥ 2Fmax .

Неравенство (6) требует ряда комментариев. Прежде всего нужно заметить, что ограничение на полосу спектров реальных сигналов всегда является определённым допущением, так как для сигналов конечной длительности (с ограниченным носителем во временной области) в частотной области спектр имеет неограниченный носитель Ων=(-∞;∞), как это следует из теоремы 2.3.

Чаще всего для определения ширины полосы спектра верхнюю частоту Fmax выбирают так, чтобы в энергетическом смысле (см. раздел 2.3) ограничение на ширину полосы не вносило больших искажений:

Fmax		∞
∫	S(ν)	2 dν = β ∫	S(ν)	2 dν , принимая значение β близким к единице
∫	S(ν)	2 dν = β ∫	S(ν)	2 dν , принимая значение β близким к единице
−Fmax		−∞

(например, β=0.9). Вне зависимости от того, из каких соображений была определена верхняя частота Fmax, перед дискретизацией сигнала целесообразно проводить низкочастотную фильтрацию с заданной частотой среза (полного подавления) fсреза=Fmax. В противном случае при восстановлении сигнала могут возникнуть недопустимые искажения.

Пример 3. Для представления речи достаточно полосы звуковых колебаний с верхней частотой F=3500 Гц. В этом случае используется стандартная частота дискретизации fд =1/ ∆t = 8000 Гц, что удовлетворяет

условию (6). Однако перед дискретизацией звуковой сигнал обязательно нужно подвергнуть НЧ-фильтрации с частотой полного подавления

fсреза ≤ 21∆t = f2Д = 4000 Гц. В противном случае может возникнуть

эффект наложения (смешения) частот. Например, если в звуковом сигнале имелась гармоническая составляющая (тон) частотой f=6000 Гц, и предварительная НЧ-фильтрация не выполнялась, то при восстановлении сигнала (обратном преобразовании из дискретного вида в аналоговый по формуле (5)) появится тон с частотой f=2000Гц, которого, возможно, в исходном звуковом сигнале вообще не было!

◄ См. пример 2, положив β=8000, α=4000. ►

Описанный эффект наложения частот (появления посторонних тонов) можно самостоятельно смоделировать с использованием мультимедийных средств персональных компьютеров.

3.4. Спектр дискретного сигнала. Спектральная иллюстрация теоремы отсчётов

Итак, выбрав определённым образом шаг дискретизации ∆t, можно получить из аналогового сигнала дискретный: f (t) →{ fk = f (k∆t)} .

Каким образом распространить понятие «частотный спектр» на дискретный сигнал – набор отсчётов {fk}? Естественно связать данное понятие с

непрерывным сигналом f (t) , который можно восстановить по дискрет-

→ ~

ному с использованием формулы (5), {fk} f (t) .

Если исходный непрерывный сигнал f(t) имел ограниченную частотную полосу и интервал дискретизации был выбран в соответствии с условием (6), то использование формулы (5) дает точное восстановление

аналогового сигнала, т.е. f(t)= f (t) , поэтому в силу свойств 2° и 4° пре-

образования Фурье спектр

можно записать в

S(ν) = Φ{ f (t)} = Φ{ f (t)}

следующем виде:

sin(2πF(t −k∆t))

∞

sin 2πFt

∞

S(ν) = ∑ f (k∆t)Φ

= Φ

∑ f (k∆t) e−2πiνk∆t .

2πF(t

−k∆t)

k =−∞

2πFt k =−∞

sin 2πFt

ν [−F; F] ,

2F ,

= ∆t , то с использованием

Так как Φ

2πFt

0 ,

ν [−F; F]

обозначения для функции «окна» ΠF (ν) = 1,ν [−F; F]

0,ν [−F; F]

∞

−2πiνk∆t

∆t

(7)

S(ν ) = ΠF (ν ) ∑ f (k∆t) e

= ΠF (ν)S (ν ) ,

k =−∞

∞

−2πiνk∆t

∆t .

(8)

S (ν ) = ∑ f (k∆t) e

k =−∞

Запись (8) уже встречалась нам при доказательстве теоремы 1. Получаем, что для функции со спектром, ограниченным частотной полосой

ν ≤ F , выражение (8) для ν [-F;F] совпадает с интегралом Фурье

S(ν) = ∫−+∞∞ f (t) e−2πiνt dt . Заметим также, что выражение (8) представляет

собой ни что иное, как квадратурную формулу прямоугольников для интеграла Фурье, узлы которой взяты в точках отчётов tk=k∆t дискретного сигнала.

Выражение (8) будем называть спектром дискретного сигнала {fk}.

Действительно, если промасштабировать дельта-функциями дискретный сигнал {fk}, преобразовав его в решетчатую функцию

f(	∞
	(t) = ∆t ∑ fkδ(t −k∆t) , то для обобщенного преобразования Фурье:

k =−∞

Φ = ~ ν

( f ) S ( ) . Отличие (7) от (8) состоит в том, что спектр дискретного

сигнала (8) является периодическим продолжением спектра S(ν) из области ν [-F;F] на всю частотную ось. Как легко видеть,

~	~	1	∆t =	1	, см. рис. 3.2. Таким образом, дискретизация
S	(ν) = S ν +	,	∆t =	2F	, см. рис. 3.2. Таким образом, дискретизация
		∆t		2F
сигнала влечёт периодизацию спектра.
					\|S(ν)\|				~
					\|S(ν)\|				S (ν)
										ν
	−1 − F			0	F	1		1
	2∆t	max			max	2∆t	∆t
Рисунок 3.2. Правильный выбор частоты дискретизации: f								=	1	≥ 2F
							Д		∆t	max

Если частота дискретизации была выбрана с нарушением условия

(6), то период функции (8) окажется меньше полосы [-F;F] исходного

ν ≠ Π ν ~ ν

сигнала и S( ) F ( )S ( ) , при этом возникают необратимые искаже-

ния сигнала, связанные с эффектом наложения частот, см. рис. 3.3.

		\|S(ν)\|		Область частотных искажений
		\|S(ν)\|		~
				S (ν)
				ν
−1	0	1	Fmax	1
− Fmax 2∆t		2∆t	Fmax	∆t

Рисунок 3.3. Неправильный выбор частоты дискретизации: fД = ∆1t < 2Fmax

3.5. Дискретное преобразование Фурье (ДПФ)

Положим, что сигнал f(t) наблюдается на конечном интервале, т.е. после дискретизации (с должным выбором шага ∆t) получаем и конеч-

ный набор отсчетов { f	k	= f (k∆t)}N −1		. Тогда в (8) получаем сумму
	k		k =0
		~	N −1	(k∆t) e	−2πiνk∆t	.	(9)
		S (ν) = ∆t ∑ f		(k∆t) e		.	(9)

k =0

Так как каждое слагаемое в сумме (9) непрерывно по переменной ν, то

~ ν

S ( ) - также непрерывная функция. Равномерно расположим на её пе-

j=0,…,N-1. То есть ν j = j∆ν , где ∆ν =ν j +1							−ν j =	1	- шаг частотной
j=0,…,N-1. То есть ν j = j∆ν , где ∆ν =ν j +1							−ν j =	N∆t	- шаг частотной
								N∆t
дискретизации. Рассмотрим			полученный				набор	частотных		отсчётов
~	~	N −1
~	= S (ν j )}j=0 . Видим:
{s j	= S (ν j )}j=0 . Видим:
		~	N −1	−	2π i	kj
		~	N −1	−	N	kj				(10)
		s j = ∆t	∑ fk e			,				(10)
j=0,…,N-1. Вектор (вообще			k =0
j=0,…,N-1. Вектор (вообще			говоря,			из	комплексных компонент)
~		~		преобразованием					Фурье	(или дис-
(s0	,K, sN −1 ) назовем дискретным			преобразованием					Фурье	(или дис-

кретным спектром) числового вектора (f0 ,K, fN −1 ). Заметим, что мож-

но также рассматривать значения частотных отсчётов (10) для любого целого j, при этом ~s j = ~s j +N .

Теорема 3. (Обратное ДПФ.) Вектор (f0 ,K, fN −1 ) можно восстановить

по дискретному спектру (10) при помощи обратного ДПФ (ОДПФ), которое определяется формулой:

N −1~	2π i	kj
N −1~	N	kj
fk = ∆ν ∑s j e		,
j =0
k=0,…,N-1.

◄ Рассмотрим правую часть равенства (11):

Имеем:

(11)

N −1~	2π i	kj
N −1~	N	kj
a(k) = ∆ν ∑s j e		.
j =0

N −1

−

2π i

N −1

2π i

j(k −m)

a(k) = ∆ν

∆t

∑

e N

= ∆ν∆t

∑

m ∑

e N

∑

123

j=0

m=0

1/ N m=0

j=0

1442443

обозначимwk ,m

Очевидно, что при k=m получаем wk,m=N. Если же k≠m, то для всех возможных значений индексов k,m=0,…,N-1 получаем, что величина

	2π i	(k −m)
q = e N		(k −m)	≠1 , и по формуле суммы геометрической прогрессии:
q = e N			≠1 , и по формуле суммы геометрической прогрессии:
			N −1 2π i				2π i(k −m)
			wk,m = ∑e		j(k −m)	= 1 − e2π i
			wk,m = ∑e	N	j(k −m)	= 1 − e2π i		(k −m)	= 0 .
			j=0
			j=0			1 −e N
						1 −e N
Поэтому			k,m=0,…,N-1:					N ,	приk = m	и
Поэтому			k,m=0,…,N-1:			wk,m =			приk ≠ m	и
								0,	приk ≠ m

1 N −1

a(k) = N m∑=0 fm wk,m = fk . ►

Мы получили следующий важный результат. Если дискретный сигнал описывается конечной последовательностью {f0 ,K, fN −1}, то вос-

~ ν

становить его по спектру S ( ) (который представляет собой непрерывную периодическую функцию частоты, см. (9)) можно, взяв лишь конеч-

	~ ~	j
ное число отсчётов спектральной плотности:	s j = S		, j=0,…,N-1.

		N∆t

Замечание. Величина T=N∆t представляет собой длину интервала наблюдения дискретного сигнала во временной области. С использованием данного обозначения можем переписать ДПФ (10):

~ N −1	−	2π i	j(k∆t)
~ N −1	−	T	j(k∆t)	∆t .
s j = ∑ f (k∆t)e				∆t .
k =0

Видим, что с точностью до множителя 1/T ДПФ (10) представляет собой квадратурную формулу прямоугольников для интеграла (2.4) - коэффициента cj ряда Фурье (2.3) функции периода T:

1 T

2πj

N −1

−

2π i

j(k∆t)

∫

f (t) exp

−i

t dt ≈

∑

f (k∆t) e

∆t =

k =0

Приближенное равенство здесь можно записать, когда период гармони-

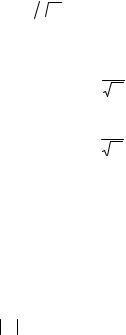
		2πj		много больше интервала дискре-
ческого колебания ω(t) = exp	−i		t
ческого колебания ω(t) = exp	−i	T	t
		T

тизации ∆t: T / j = N∆t / j >> ∆t j << N .

Таким образом, (10) и (11) – это взаимно обратные преобразования (вообще говоря, комплекснозначных) векторов: (f0 ,K, fN −1 )↔(~s0 ,K, ~sN −1 ). Если теперь отвлечься от природы этих век-

торов (временные и частотные выборки), то величины ∆t в (10) и ∆ν в (11) есть просто некоторые масштабные множители, такие, что ∆t∆ν=1/N (данное равенство также несёт в себе смысл время-частотной неопределённости дискретного представления сигнала!). Для симметрии поло-

жим ∆t = ∆ν =1 N и парой ДПФ-ОДПФ будем называть преобразо-

вания векторов (x0 ,K, xN −1 )↔(y0 ,K, yN −1 ), где ДПФ и ОДПФ определяются соответственно:


	1	N∑−1x j e−		2π i		kj ,
yk =	1	N∑−1x j e−		N		kj ,	(12)
	N j =0
k = 0,K, N −1,
	1	N∑−1yk e	2π i		kj ,
x j =	1	N∑−1yk e	N		kj ,		(13)
	N	k =0
j = 0,K, N −1.

Как уже отмечалось, в радиотехнике и электронике частотное описание аналоговых сигналов во многих случаях более предпочтительно. Для дискретных сигналов, как мы показали, спектр определяется выражением (8), причём для конечных интервалов наблюдения сигнала последний можно однозначно описать через ОДПФ (13) частотными отсчётами спектральной функции (8), для нахождения которых используется ДПФ (12). Таким образом, определяемый через ДПФ (12) дискретный спектр является аналогом интегрального преобразования Фурье (2.6). Точно также, термин «амплитудный спектр» употребляется для

модулей {yk }kN=−01 спектральных коэффициентов (12), «фазовый спектр»

- для аргументов, взятых с противоположным знаком: {−arg yk }kN=−01 . Пусть Y = (y0 ,K, yN −1 ) – дискретный спектр, полученный из век-

тора X = (x0 ,K, xN −1 ) в результате ДПФ (12), X↔Y. Отметим важные свойства ДПФ.

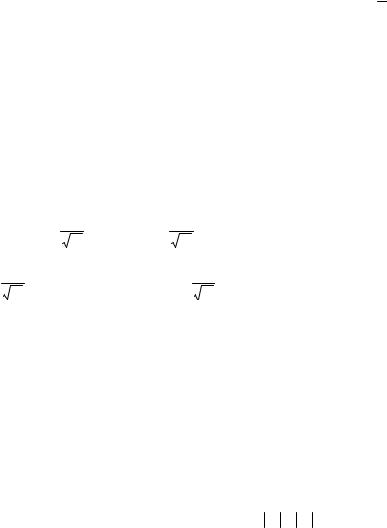
1°. Сопряженная симметрия. Для любого вещественного вектора X = X в векторе-спектре y0 = y0 (компонента вещественная), а

k =1,K, N yk = yN −k .

◄ Докажите самостоятельно. ►

2°. Линейность. X1 ↔ Y1, X2 ↔ Y2 , α, β :

X = αX1 + βX2 ↔ Y = αY1 + βY2 .

3°. Циклический сдвиг влево. Сдвигу компонент вектора-сигнала:

X = (x0 , x1K, xN −1 )→ X′ = (x1K, xN −1, x0 ) в области дискретного спектра соответствует такое изменение

Y = (y0 , y1K, yN −1 )→ Y′ = (y0′, y1′K, y′N −1 ), что k yk′ = ei

2πk

yk .

◄ yk′ = 1

N −1

2π i

kj =

N −2

2π i

kj + x0 e

2π i

k ( N −1)

∑x′j e−

∑ x j+1 e−

−

N j=0

j =0

N −1

−

2π i

k( j−1)

2π i

2πi

N −1

−

2πi

∑x j e

+ x0 e

= e

. ►

∑x j e

N j=1

j=0

Следствие. Циклический сдвиг влево на m позиций.

2πk

X′ = (xm , xm+1,K, xN −1, x0 , x1,K, xm−1) ↔ Y′: k yk′

= e

yk .

4°. Циклический сдвиг вправо на m позиций. Сдвигу компонент вектора-

сигнала:
X = (x0 , x1K, xN −1 )→ X′ = (xN −m ,K, xN −2 , xN −1, x0 ,K, xN −m−1 ) в об-
ласти дискретного спектра соответствует	такое	изменение
Y = (y0 , y1K, yN −1 )→ Y′ = (y0′, y1′K, y′N −1 ), что		−i	2πk	m
	k yk′	= e	N		yk .

◄ Докажите самостоятельно. ►

Следствие из свойств 3° и 4°. Инвариантность амплитудного спектра относительно циклических сдвигов: k yk = yk′ .

Определение. Под дискретной сверткой векторов

A = (a0 , a1,K, aN −1 ) и B = (b0 ,b1,K,bN −1 ) будем понимать вектор C = (c0 ,c1,K,c2N −1 ) вдвое большей размерности, компоненты ко-

торого определяются по формуле:

N −1	N −1
ck = ∑a jbk − j = ∑ak − jbj		(14)
j =0	j =0

(k=0,1,…,2N-1), где предполагается, что am = bm = 0 , если значение индекса m выходит за допустимые границы (при m<0 или m>N-1).

5°. Свойство ДПФ свертки векторов.

Обозначим A = (a

,K, a

(

, 0,K,0) ,

N −1

,0,K,0) , B = (b ,K,b

−1

123

N нулей

2N −1

(

−

2π i

– ДПФ вектора A , aˆk =

A = (aˆ0 ,aˆ1,K,aˆ2N −1)

∑ a j e

j=0

ˆ ˆ

(

2N −1 (

−

2π i

B =

(b0 ,b1,K,b2N

−1) – ДПФ вектора B

, bk

∑ bj e

j =0

Тогда для вектора C – свертки векторов A и B (14) – ДПФ

−1) можно найти перемножением компонент век-

C = (cˆ0 ,cˆ1,K, cˆ2N

торов

k cˆk

и B :

2N aˆk bk .

−

2π i

◄ Обозначим

= e

Для

ДПФ

вектора-свертки

имеем:

2N −1

2N −1 N −1

N −1 2N −1

cˆk =

∑cjω

∑

∑am ∑bj−mω

∑ambj−m ω

j=0

2N j=0

m=0

2N m=0

j=0

N −1

2N −1−m

N −1

−1

∑am

∑blωk (l +m) =

∑amωkm

∑blωkl ,

2N m=0

l =−m

2N m=0

l =0

поскольку

bl=0

при

l<0

или

l>N-1.

замечаем, что

N −1

2N −1(

и, аналогично,

N −1

2N aˆk . ►

∑blω

2N bk

∑amω

l =0

m=0

ДПФ (12) и ОДПФ (13) удобно записывать в матричном виде, пред-

ставив

как

векторы-столбцы:

X = (x0 ,K, xN −1 )T ,

Y = (y0 ,K, yN −1 )T .

Тогда ДПФ и ОДПФ,

соответственно,

принимают

вид:

Y = WX ,

X =

где

матрица

ДПФ

WY ,

<<< < Предыдущая 1 2 3 4 56 / 186 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>