книжка умняшкина по моцос

Добавил:

korayakov Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

Математическое обеспечение цифровой обработки и кодирование сигналов

Файл:

aN ,n = aN ,n +O(2

где aN ,n = f (xn ) ∫φN ,n (x)dx = f (xn )

∫φ(x)dx , ∆k

- носитель функ-

.pdf

Скачиваний:

133

Добавлен:

16.04.2013

Размер:

1.55 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 1817 18 > Следующая >>>

На практике число шагов алгоритма вейвлет-преобразования (количество повторений процедур (17), (18)) должно быть конечно. Для некоторого числа m=K вычисления прекращаются, то есть вместо разложения (13) мы ограничиваемся представлением:

∞	M −1 ∞
fM (x) = ∑aK ,nφK ,n (x) + ∑ ∑cm,nψm,n (x) =
n=−∞	m=K n=−∞
1442443	1442443
f K ( x) VK	ym ( x) Wm
= fK (x) + yK (x) + yK +1(x) +KyM −1(x) .		(19)

Обычно K выбирается так, чтобы коэффициенты aK ,n = ∫ f (x)φK ,n (x)dx

∆Kn

(предполагается, что носитель ∆Kn функции φK ,n (x) - конечный отрезок)

«грубой» проекции fK(x) VK можно было считать некоррелированными.

Так, если L – длина интервала корреляции для сигнала f(x) (то есть x0,

τ >L значения функции в точках f(x0) и f(x0+τ) считаются некоррелированными), то выбирать K следует так, чтобы носитель ∆Kn представлял

собой отрезок, длина которого много больше L:	∆Kn	=	1	∆00	>> L .

			2K

Формулы (17), (18) представляют собой соотношения декомпози-

ции, используемые для получения вейвлет-разложения функций. Рассмотрим теперь обратную задачу (композиции) и получим соотношения, которые обращают (17) и (18), т.е. по заданным своими коэффициентами Фурье разложениям

fm−1(x) = ∑am−1,nφm−1,n (x) ,			ym−1(x) = ∑cm−1,nψm−1,n (x)
	n Ζ			n Ζ
позволяют	найти	коэффициенты		{am,n}n Z	функции

fm (x) = ∑am,nφm,n (x) . Для этого в правую часть уравнения (14) подста-

n Ζ

вим выражения для φm−1,n (x) , ψm−1,n (x) , определяемые формулами (15) и (16), и полученное равенство скалярно умножим на функцию φm,k (x) :

∑am,n < φm,n (x),φm,k (x) > =

	n Ζ
= ∑am−1,n < ∑hj−2nφm, j (x),φm,k (x) >+ ∑cm−1,n < ∑g j−2nφm, j (x),φm,k (x) > .
n Ζ	j Z	n Ζ	j Z
	1442443		1442443
	φm−1,n ( x)		ψm−1,n ( x)

161

Отсюда вследствие ортонормированности системы {φm,k (x)}k Ζ Vm получаем k:

am,k = ∑am−1,nhk −2n + ∑cm−1,n gk −2n .		(20)
n Ζ	n Ζ

Последовательно применяя формулу (20) к парам последовательно-

стей ({am,n}n Z, {cm,n}n Z), m=K+1,…,M, по коэффициентам разложения (19) можем восстановить коэффициенты {aM,n}n Z, задающие проекцию

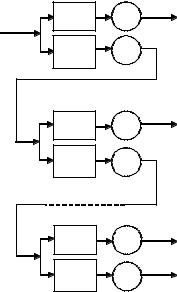
fM(x) VM. Соответствующую последовательность вычислений можно представить в виде следующей схемы (рис. 7.2).

yK ↔{cK ,n}

yK −1 ↔{cK −1,n}

	(20)		(20)	(20)
fK ↔{aK ,n}		fK −1 ↔{aK −1,n}			fM ↔{aM ,n}

Рисунок 7.2. Схема вычисления обратного вейвлет-преобразования

Как упоминалось в разделе 7.1, знания коэффициентов {hn} масштабирующего уравнения (1) достаточно для того, чтобы задать функцию φ(x). Покажем это. Из формулы (8) и леммы 2 следует, что

ции φj,k(x), xn – середина отрезка ∆Nn , причем n : h=xn+1-xn=1/2N. Поэтому можем записать для отсчетов функции f(xn), взятых с шагом h:

f (xn ) = C2N / 2 aN ,n +O(h) ,	(21)
где C = 1 ∫φ(x)dx . Отсюда видим, что, имея набор	коэффициентов
∆00

{aN,n}n Z, который характеризует проекцию fN=AN(f) VN, можно с погрешностью порядка O(h) найти значения функции f в точках xn, взятых с шагом h=1/2N. То есть, увеличивая N, можно как угодно точно описать функцию f(x): погрешность определения значения функции в отсчетах f(xn) по формуле (21) будет уменьшаться, а сами отсчеты будут располагаться на числовой оси все более часто.

162

С учетом (20) и (21) процедура нахождения масштабирующей функции φ(x) при известном наборе коэффициентов {hn} состоит в следующем. Положим, что в выражении (21) С=1. Так как φ(x) =φ0,0 (x) - базисная функция пространства V0, то в разложении (4) функции

φ(x)=f0(x) V0 получим a0,0=1, k≠0: a0,k=0. При этом в представлении

φ(x)=f0(x)+y0(x), где f0(x) V0, y0(x) W0, получаем y0(x)=θ и k: с0,k=0. То-

гда с использованием формулы (20) можем найти коэффициенты

{a1,k}k Z разложения масштабирующей функции φ(x) V0 V1 V2 … по базису пространства V1. Рекуррентно применяя полученную из (20)

формулу

am,k = ∑am−1,nhk −2n n Ζ

далее для m=2,3,…,N, можно получить как угодно точное описание масштабирующей функции φ(x), для чего нужно воспользоваться соотношением (21), положив φ(x)=f(x). Константу С (масштаб по оси абсцисс) окончательно нужно будет выбрать так, чтобы выполнялось условие

+∞

нормировки масштабирующей функции: φ(x) 2 = ∫φ2 (x)dx =1 .

−∞

Задание. По аналогии с описанной процедурой итерационного построения масштабирующей функции опишите процедуру нахождения материнского вейвлета ψ(x) W0 V1 V2 … по заданному набору коэффициентов {hn} масштабирующего уравнения (1) и коэффициентов

{ gn = (−1)1−n h1−n } уравнения (3).

7.4. Квадратурно-зеркальные фильтры

Вернемся к рассмотрению формулы (17), которая задает преобразование некоторой входной последовательности x(n)=am,n в выходную

y(k)=am-1,k.		Пусть j=2k – четное	число (k Z). Тогда	обозначив
~	~	= h−m , можем переписать (17) в следующем виде:
h (m) = hm		= h−m , можем переписать (17) в следующем виде:
		∞	~	(22)
		y( j / 2) = ∑x(n)h ( j −n) .		(22)

n=−∞

Сравнивая полученное выражение с формулой (4.9), приходим к выводу, что преобразование последовательности x(n) в y(k) можно трактовать как линейную фильтрацию, при помощи дискретного фильтра с импульсной

163

~ = ~

характеристикой (ИХ) { h (n) hn }, с последующим прореживанием откли-

ка фильтра, при котором сохраняются только отсчеты с четными номерами, см. рисунок 7.3. Для операции прореживания, отбрасывающей нечетные номера последовательности, будем использовать обозначение ↓2.

x(n)	~	y(j), j Z	↓2	y(k=j/2)
n Z	h (m) = h−m		↓2	k Z
				k Z
	Линейная	Прореживание
	Линейная	Прореживание
	фильтрация

Рисунок 7.3. Схема реализации процедуры (22) при помощи дискретного фильтра и прореживания последовательности

При рассмотрении операции (22) с точки зрения теории линейных
дискретных систем возможна ситуация, когда ИХ	~	~
	h (n) = hn ≠0 при n<0,

что соответствует физически нереализуемой системе (нарушение при- чинно-следственной связи: отклик на выходе появляется раньше сигнала на входе). Однако теоретическое рассмотрение подобных систем корректно и противоречия в этом нет, поскольку номера индексов элементов обрабатываемых последовательностей не следует обязательно отождествлять с моментами времени, а линейное преобразование последовательностей по формуле (22) с реальным физическим устройством.

Все рассуждения, касающиеся трактовки формулы (17), можно повторить и для формулы (18), тогда один шаг алгоритма вычисления коэффициентов вейвлет-разложения (см. рис. 7.1) можно представить как параллельную обработку фильтрами с импульсными характеристиками

~	~		прореживание выходных
{ h (n) = h−n },	{ g(n) = g−n } и последующее
последовательностей, см. рис. 7.4.
	~	↓2	fj-1 Vj-1:
			{…,aj-1,k,aj-1,k+1,…}
fj Vj:	h (n) = h−n

{…,aj,k,aj,k+1,…}			yj-1 Wj-1:
	~	↓2
	g(n) = g−n		{…,cj-1,k,cj-1,k+1,…}

Рисунок 7.4. Реализация одного шага вейвлет-преобразования (17), (18)

164

При этом, если входная последовательность {…,aj,k,aj,k+1,…} была конечна и состояла из 2L элементов, то в результате реализации процедуры

рис. 7.4. получим 2 последовательности из L элементов каждая.

Пример 4. Для КМА из примера 1 найти выходные последовательности в схеме обработки рис. 7.4 для входного воздействия

{x(0), x(1), …, x(2L-1)}.

◄ Воспользовавшись результатами примера 1, получаем следующие

~					~
~		2,1		,	~
ИХ: h(n) = K,0,0,1		2,1	2,0,0,K	,	g(n) = K,0,0,	−1 2,1 2,0,0,K .
	123 123					123 123
	~	~	(0)			~	~
	h	(−1) h	(0)			g (−1)	g (0)

Отклики фильтров находим по формулам свертки, которые принимают вид:

0 ~	(n)x(k −n) =	x(k) + x(k +1)	,
u(k) = ∑h		2
n=−1
0 ~	(n)x(k −n) =	x(k) − x(k +1)	.
v(k) = ∑g		2
n=−1

Тогда после прореживания, сохраняющего лишь четные номера выходных последовательностей, {u(2k)} и {v(2k)}, и всей обработки по схеме рис. 7.4 из одной входной последовательности {x(0), x(1), …, x(2L)} по-

лучим две выходных:	x(2k) + x(2k +1)		L−1	,	x(2k) − x(2k +1)		L−1
		2				2		. ►
			k =0				k =0

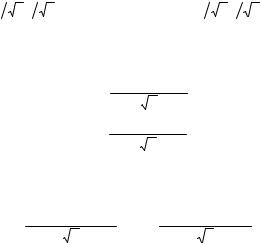
Каскадируя блоки фильтров рис. 7.4, можно выполнить вейвлетразложение на любую «глубину», т.е. до любого уровня разрешения проекции fK(x) VK, заданной набором коэффициентов {aK,k}, см. рис. 7.5.

165

fj Vj:	~	↓2	yj-1 Wj-1:
	g(n)		{…,cj-1,k,cj-1,k+1,…}
{…,aj,k,aj,k+1,…}
	~	↓2

	h (n)

fj-1 Vj-1:

{…,aj-1,k,aj-1,k+1,…}

…

fK+1 VK+1: {…,aK+1,k,aK+1,k+1,…

~	↓2	yj-2 Wj-2:
g(n)	↓2	{…,cj-2,k,cj-2,k+1,…}
~	↓2
h (n)	↓2
		…
~		yK WK:
~	↓2	{…,cK,k,cK,k+1,…}
g(n)	↓2	{…,cK,k,cK,k+1,…}
~	↓2	fK VK:
h (n)	↓2	fK VK:
		{…,aK,k,aK,k+1,…}

Рисунок 7.5. Вычисление вейвлет-преобразования при помощи блоков фильтров

Рассмотрим теперь формулу (20), которая обращает процедуру, определяемую формулами (17), (18) и рисунком 7.4. Обозначим: j=2n,

b(2n)=am-1,n, b(2n+1)=0, hm=h(m), тогда для первой суммы в формуле (20) получим:

∞	∞	∞
S1 (k) = ∑am−1,n hk −2n =	∑b(2n)h(k − 2n) =	∑b( j)h(k − j) , (23)
n=−∞	n=−∞	j=−∞

что можно представить как отклик линейного фильтра с ИХ h(n), на вход которого подана последовательность {b(j)}, полученная добавлением одного нуля после каждого элемента последовательности {am-1,n}n Z. Аналогично, вторую сумму в формуле (20) можем записать как

		∞		∞
	S2 (k) = ∑cm−1,n gk −2n = ∑d( j)g(k − j) ,
	n=−∞			j=−∞
где gm=g(m),	c	m−1, j / 2	, если j	− четноечисло	.
где gm=g(m),	d( j) =	m−1, j / 2		нечетноечисло	.
		0, если j −		нечетноечисло
166

Операцию вставки нулевого элемента на каждую вторую позицию в последовательности обозначим ↑2. Тогда вычислениям по формуле (20) соответствует схема обработки, которая реализуется при помощи двух фильтров с импульсными характеристиками h(n) и g(n), см. рис. 7.6.

fj-1 Vj-1:	↑2	h(n) = hn
{…,aj-1,k,aj-1,k+1,…}	↑2	h(n) = hn
		fj Wj:
yj-1 Wj-1:		{…,aj,k,aj,k+1,…}
yj-1 Wj-1:	↑2	g(n) = gn
{…,cj-1,k,cj-1,k+1,…}	↑2	g(n) = gn

Рисунок 7.6. Реализация процедуры (20) при помощи дискретных фильтров

Схема обработки, представленная на рисунке 7.6, является обратной процедурой для схемы обработки последовательности, приведенной ранее на рисунке 7.4. Поэтому обращение многоуровневого преобразования, схема которого отражена на рис. 7.5, также достигается каскадированием соответствующих структурных блоков фильтров, см. рис. 7.7.

yj-1 Wj-1:	↑2	g(n) = gn
{…,cj-1,k,cj-1,k+1,…}	↑2	g(n) = gn	fj Wj:
			fj Wj:
fj-1 Vj-1:			{…,aj,k,aj,k+1,…}
{…,a j-1,k,a j-1,k+1,…}	↑2	h(n) = hn
…			…
yK WK:	↑2	g(n) = gn
{…,cK,k,cK,k+1,…}	↑2	g(n) = gn	fK+1 VK+1:
fK VK:			{…,aK+1,k,aK+1,k+1,…}
fK VK:	↑2	h(n) = hn
{…,aK,k,aK,k+1,…}	↑2	h(n) = hn

Рисунок 7.7. Вычисление обратного вейвлет-преобразования при помощи блоков зеркальных фильтров

167

~	Для импульсных характеристик фильтров рис. 7.4 и рис. 7.6 верно:
	~
g(n) = g(−n) , h (n) = h(−n) , т.е. ИХ являются зеркальными. Все вместе
эти	четыре фильтра называют квадратурно-зеркальными фильтрами

(КЗФ). Описать данные фильтры можно не только при помощи ИХ, но и

~ ~

задав передаточные функции H (z) , G(z) , H (z) , G(z) , или частотные

характеристики K ~ (ω) , K ~ (ω) , KH (ω) , KG (ω) . Выясним, как связаны

H G

∞

частотные характеристики КЗФ. Если KH (ω) = ∑h(k)e−iωk - частотная

k =−∞

характеристика (ЧХ) фильтра (см. раздел ИХ h(n)=hn, то для зеркального фильтра, пряжена:

	∞	−iωk		∞
KH (ω) =	∑h(−k) e	−iωk	=	∑h(k
~
	k =−∞			k =−∞

4.5), имеющего вещественную очевидно, ЧХ комплексно со-

) eiωk = KH (ω) .

∞

Аналогично: KG (ω) = ∑g(k) e−iωk , K ~ (ω) = KG (ω) . Таким образом,

k =−∞

АЧХ зеркальных фильтров одинаковы, а в ФЧХ имеем отличие в знаке. Напомним, что ЧХ является 2π-периодической функцией (см. раздел 4.5). Учитывая (см. раздел 7.1), что ИХ КЗФ связаны соотношением

gn = (−1)

−n

h1−n ,

или gn

1−n

h1−n ,

и G фильтров полу-

= (−1)

для АЧХ G

чаем:

∞

K ~

(ω)

∑

(−1)1−k h

e−iωk

∑

h (−1)n e−iω(1−n)

1−k

n {

k =−∞

n=−∞

eiπ

−iω

∞

i(ω+π )n

∞

i(ω+π )n

= e

∑hn e

= ∑hn e

(ω +π)

KH (ω +π)

n=−∞

Поэтому (см. иллюстрации из раздела 4.5) если фильтры H и H являют-

ся низкочастотными, то фильтры G и G будут высокочастотными. Пример 5. Построить графики АЧХ KH (ω) и KG (ω) для КЗФ, опре-

деляемых вейвлетом Хаара (см. пример 1). ◄ В данном случае

(ω) = KH (ω) =

e−iω

−

iω

eiω 2 +e−iω 2

= 2 cos

= 1+cosω ,

168

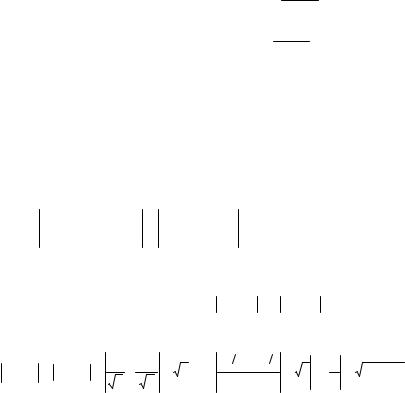
KG (ω) = KG (ω) =	1+cos(ω +π) =	1−cosω = 2 sin		ω	.
~				2
				2
Графики АЧХ приведены на рис. 7.8.
		2	KG(ω)		KH(ω)
		2

Отметим, не доказывая, что и для других КЗФ также сохраняется

свойство ЧХ, которое мы наблюдаем в примере 5: H и H фильтры яв-

ляются низкочастотными, а G и G – высокочастотными. Процедуру фильтрации дискретного сигнала парой фильтров рис. 7.4 с частотной точки зрения можно пояснить как «расщепление» частотного спектра дискретного сигнала - последовательности {…,aj,k,aj,k+1,…} на два рав-

ных частотных поддиапазона: низкочастотного (отклик H -фильтра) и

высокочастотного (отклик G -фильтра). При этом (в идеале!) если для входной последовательности максимально возможная верхняя частота

сигнала была равна Fв=FД/2 (половина частоты дискретизации), то час-

тотный спектр отклика H -фильтра будет иметь вдвое меньшую верхнюю частоту.

7.5. Биортогональные вейвлет-преобразования

Требование конечности сумм в формулах (17), (18) (и, соответственно, (1), (3)), необходимое для численной реализации дискретного вейвлет-преобразования, существенно снижает возможности выбора вейвлет-базисов, ограничивая их базисами с финитным носителем. Поэтому мы уже неоднократно предполагали конечность носителя вейвлета и масштабирующей функции при построении многих рассуждений, поскольку для практических приложений данное свойство обычно является необходимым.

169

Ортогональные базисы вейвлетов с финитным носителем (базисы Добеши) не всегда оказываются наиболее удобными для представления сигналов. Более широкое распространение на практике получили финитные вейвлет-базисы с «ослабленными» требованиями к ортогональности, так называемые биортогональные базисы. В этом случае функциональные базисы масштабирующих функций {ϕm,n } Vm и вейвлетов

{ψm,n } Wm уже не являются ортогональными, однако в тех же пространствах для них существует дуальная пара базисов (также неортого-

нальных)	{ϕm,n } Vm ,	{ψm,n } Wm таких,		что < ϕm,n ,ϕm,k >= δn,k ,
	~	~		~
<ψ~m,n ,ψm,k >= δn,k , где		δn,k	1, при n = k	.
<ψ~m,n ,ψm,k >= δn,k , где		δn,k	=	.
			0,при n ≠ k

Биортогональные базисы обладают взаимной симметрией. Поиск коэффициентов разложения по одному из базисов дуальной пары состоит в вычислении скалярных произведений f(x) и функций другого дуального базиса. Так, если

f (x) = ∑cm,nψm,n (x) ,

(23)

n,m Ζ

то cm,n =< f ,ψ~m,n > (убедитесь!).

При использовании биортогональных базисов коэффициенты в формулах декомпозиции (17), (18) и реконструкции (20) могут отличаться, хотя схема вычислений остается совершенно той же. Декомпозиция, которую вновь можно трактовать как линейную фильтрацию с последующим прореживанием последовательностей, осуществляется с использованием формул

= ∑∞ ~

am−1,k am,nh2k −n ,

n=−∞
∞	~

cm−1,k = ∑am,n g2k −n ,

n=−∞

аформула восстановления (20) сохраняет в точности тот же вид, причем

~ ≠

для биортогональных преобразований, вообще говоря, hj h− j , g~ j ≠ g~− j и, более того, количество ненулевых коэффициентов в им-

пульсных характеристиках фильтров декомпозиции и в фильтрах реконструкции может быть различным. Но между коэффициентами биортого-

нальных фильтров существует следующая связь:	~	n+1	h−n+1	,
нальных фильтров существует следующая связь:	gn = (−1)		h−n+1	,
170

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 1817 18 > Следующая >>>