Глава 4. Энтальпия. Расчет изменения внутренней энергии, энтальпии и энтропии. Графический метод в термодинамике

Одной из энергетических характеристик термодинамической системы является тепловая функцияили энтальпия. Выражение для энтальпии можно получить из первого закона термодинамики

dQ = dU + pdV (4.1)

Так как d(pV) = pdV + Vdp, то pdV = d(pV) - Vdp. Подставляя это значение pdV в уравнение (4.1) , получим

dQ = dU + d(pV) - Vdp = d(U + pV) - Vdp (4.2)

Сумма (U + pV) = Iи является энальпией. С учетом выражения для энтальпии уравнение (4.2) можно записать в следующем виде

dQ = dI - Vdp (4.3)

свойства энтальпии:

- энтальпия системы является однозначной функцией состояния системы;

- дифференциал dI является полным дифференциалом;

- энтальпия является аддитивной величиной ;

энтальпия тела определяется в термодинамике с точностью до некоторой постоянной слагающей. Для изохорного процесса (C = Cv и dV = 0) на основании уравнения (4.1) имеем dU = C_vdT (4.4)

Аналогично из уравнения (4.3) для изобарного процесса получаем

dI = C_pdT (4.5)

Первый закон термодинамики справедлив для веществ с любыми свойствами, поэтому по уравнению (4.4) в изохорном процессе, а по уравнению (4.5) в изобарном процессе соответственно dU и dI можно рассчитывать для веществ с любыми свойствами.

Формулы для расчета изменения энтропии идеального газа

1. dQ = dU + pdV или TdS = CvdT + pdV (4.6)

Из последнего уравнения следует

dS = C_v (4.6а)

После интегрирования уравнения (4.6а) получим

S₂- S₁= (4.7)

2. dQ = dI - Vdp или TdS = C_pdT - Vdp (4.8)

Из формулы (4.8) следует

dS = C_p (4.9)

Из формулы (4.9) следует

S₂- S₁ = (4.10)

Графический метод в термодинамике

Равновесное состояние системы можно отобразить графически в различных системах координат:p - V - T;T - S - Vи др. На рис. 4.1 в координатахp - V - Tзаданное равновесное состояние отображено точкойА. Под влиянием внешнего воздействия газ будет изменять свое состояние, в результате чего координаты точки будут изменяться. Соединив множество точек, характеризующих различные состояния, получим некоторую термодинамическую поверхность. Уравнением термодинамической поверхности является уравнение состояния. Если в термодинамическом процессе изменяются все три параметра газа ( p , V , T ), то этот процесс изобразится вp - V - Tкоординатах пространственной кривой, расположенной на термодинамической поверхности.

Диаграмма p - Vпримечательна тем, что в этих координатах площадь под кривой, характеризующей процесс, определяет работу, совершаемую газа при расширении, или работу, затраченную на сжатие. Действительно, площадка под элементарным процессом (рис. 4.2) есть работа A = pdV. Полная работа в процессе1-2будет равна

A = (4.11)

Рис. 4.2 Рис. 4.3

Процесс можно рассматривать и в координатах T - S - V. Проекция пространственной кривой на плоскость T - S даст плоскую кривую. Представление процесса в координатах T - S дает возможность определить количество теплоты, подведенное к системе (dS >0) из внешней среды, или отведенное от нее в окружающую среду (dS<0). Площадь под элементарным процессом равна TdS, т.е. количеству теплоты dQ, рис. 4.3.

Полное количество теплоты в процессе 1-2 может быть представлено следующим выражением Q = .

T - S диаграмма для идеального газа

Из формулы (4.7) следует, что в изохорном процессе

(DS)_v = (4.12)

Для изобарного процесса из формулы (4.10) имеем

(DS)_p = (C_p) (4.13)

Из уравнений (4.12) и (4.13) видно , что в T - S координатах изохоры и изобары представляют собой логарифмические линии. Тангенс угла наклона касательной к изохоре и изобаре получим соответственно из соотношений (4.6) и (4.8): tga_v = (¶T/¶S)_v= T/C_v ; tga_p = (¶T/¶S)_p= T/C_p. Отсюда следует, что с ростом температуры тангенсы углов наклона касательной и изохоре tga_v и к изобаре tga_pувеличиваются. Поэтому кривые обращены выпуклостью вниз. Так как C_p >C_v, то tga_v >tga_p , рис. 4.4. Для того, чтобы определит расстояние по горизонтали между двумя соседними изохорами и соседними изобарами воспользуемся формулами (4.7) и (4.10), из которых следует, что при постоянной температуреDS)_T= R ln V₁/V₂и (DS)_T= - R ln p₂/p₁.

Следовательно, изохоры больших объёмов располагаются правее от основной изохоры, а меньших объёмов - левее. Следовательно область низких давлений располагается правее от основной изобары, а область высоких давлений - левее.

Расстояние между основной изохорой и изохорами двойного, тройного и больших объёмов равны R ln2, R ln3 и так далее. Расстояние между изобарами: -R ln2, R ln3 и так далее.

Процессы при постоянной температуре (изотермические) изображаются горизонтальными линиями (рис. 4.5). В изотермических процессах с идеальным газомDU = 0, поэтому теплота подведенная к газу расходуется только на работу расширения. Следовательно процесс А - В (DS>0) - изотермическое расширение, а процесс А - С - изотермическое сжатие. Процессы , протекающие без теплообмена с окружающей средой (Q = 0;DS = 0), называются адиабатными и изображаются вертикальными линиями. В этих процессах в соответствии с первым законом термодинамики, работа совершается за счет внутренней энергии (dQ = - dU). Уменьшение внутренней энергии влечет за собой снижение температуры. Следовательно процесс 1-2 - адиабатное расширение, а процесс 1-3 - адиабатное сжатие. При адиабатном сжатии работа, затраченная на сжатие преобразуется во внутреннюю энергию газа, следствием чего является повышение температуры газа. Все выше рассмотренные процессы относятся к равновесным.

При неравновесном адиабатном расширении (1-4) или сжатии (1-5) вследствие выделения теплоты трения энтропия увеличивается. При этом, в процессе неравновесного адиабатного расширения газ совершает меньшую работу, чем в равновесном, так как часть энергии газа расходуется на преодоление сопротивления трения. При неравновесном сжатии работа затрачивается большая, по сравнению с равновесным процессом.

Действительно, в процессе расширения:

A_1-2 = -DU_1-2= -и A_1-4= -DU_1-4= -

Откуда следует, что А_1-2>А_1-4

При сжатии:

A_1-3=-DU_1-3=и A_1-5= -DU_{1- 5} = -

Откуда следует, что А_1-3<А_1-5.

I - S диаграмма для идеального газа

В I-S координатах так же как и в T-S изохоры и изобары изображаются логарифмическими линиями. Из соотношения (4.12) следует, что тангенс угла наклона касательной к изобаре в I-S координатах (tga)_p= (¶I/¶S)_p= T. Следовательно, с ростом температуры значение (tga)_p увеличивается т. е. изобары обращены выпуклостью вниз, как и в T-S координатах. Изотермы в правой части диаграммы представляют собой прямые горизонтальные линии, которые изгибаются в левой части диаграммы (рис. 4.6) . Такой ход изотерм объясняется тем, что при низких давлениях (правая часть диаграммы) газ ведет себя как идеальный газ, для которого энтальпия является функцией только температуры, область высоких давлений (левая часть диаграммы) - область реального газа, при котором энтальпия зависит не только от температуры , но и от давления.

Анализ составляющих уравнения первого закона термодинамики

dQ = dU + pdV = dU + dA

Внутренняя энергия является функцией состояния, поэтому изменение её не зависит от пути, по которому рабочее тело перешло из одного состояния в другое, рис. 4.7.

DU_1-a-2=DU_1-b-2=DU_1-c-2

следовательно, dU есть полный дифференциал функции U, значение которой однозначно определяется заданием всех координат состояния U=U(x₁,x₂,...., x_m).Для термодеформационной системы = U(S,V). Как видно из рис. 4.7 работа, т. е. А, в указанных процессах (площадь под кривой, описывающей процесс) различная. Аналогично и количество теплоты Q в T-S координатах будет отличаться друг от друга в зависимости от вида процесса. Следовательно, dQ и dA в уравнении первого закона термодинамики не являются полными дифференциалами, а представляют собой элементарные количества теплоты и работы.

Глава 5. Разомкнутые термодинамические процессы. Круговые процессы (циклы). Особенности тепловых и холодильных машин. термический коэффициент полезного действия цикла тепловой и холодильной машин. Цикл и теорема Карно.

Очевидно, что изменение состояния системы возможно только в результате её взаимодействия с окружающей средой. Закон изменения состояния зависит от характера внешних воздействий, т. е. от того в каких формах происходит обмен энергией системы с окружающей средой и в каких соотношениях между собой находятся значения количеств взаимодействий. Для термодеформационного взаимодействия системы, варьируя количеством теплоты и работы, можно осуществить любой закон изменения состояния газа.

Например, на рис.5.1 в T-S координатах изображены три процесса, в каждом из которых теплота подводится (dS>0). При этом температура в процессе 1-2 повышается, а в процессе 1-4 понижается. Это является следствием того, что в процессе 1-2 количество подведенной теплоты больше совершенной газом работы (Q>А), поэтому часть теплоты затрачивается на повышение внутренней энергии газа, в результате чего его температура повышается. В процессе 1-4 Q<A , следовательно часть работы совершается за счет внутренней энергии газа, и температура последнего понижается. В процессе 1-3 для идеального газа dU = 0 , поэтому Q = A.Процесс изменения состояния газа при заданном в нем соотношении между Q и A называется политропным процессом. Множество процессов с различными значениями соотношения Q/A можно обобщить одним уравнением - уравнением политропного процесса или кратко - уравнением политропы

(5.1)

Здесь n - показатель политропы, значение которого остается неизменным в данном процессе.

Вывод уравнения политропы, как и других термодинамических соотношений, основан на первом законе термодинамики.

dQ = dU + dA или CdT = C_vdT + pdV. Вынося за скобки dT, получим

(С - С_v) dT - pdV = 0 (5.2)

Дифференцируя уравнение состояния идеального газа pV = RT, получим

dT = (pdV + Vdp) / R. Подставим это значение dT в уравнение (5.2)

(5.3)

Так как R = C_p - C_v, то подставив это значение в уравнение (5.3), получим

(5.4)

Обозначим , и поделив (5.4) на произведение pV, получим

. После интегрирования полученного соотношения находим окончательный результатили(5.5)

Из уравнения (5.5) следует , что для :

- изобарного процесса (p = Const) n = 0

- изотермического процесса (T = Const) n = 1,0.

В адиабатном процессе - Q = 0, следовательно, С = 0 и показатель политропы - показатель адиабаты , значение которого для двухатомных газов при относительно невысоких температурах равно 1,4 , а для трехатомных газов

k = 1,3. k =

C увеличением температуры теплоёмкость газов увеличивается, поэтому значение k уменьшается, однако очень незначительно.

Извлечением корня n- ой степени (см. уравнение (5.5)) получим

. Следовательно , в изохорном процессе (V = Const ) величина n =¥. На рис. 5.2 и 5.3 рассматриваемые процессы представлены в p-V и T-S координатах.

Соотношения между параметрами в политропном процессе

На основании закона Бойля-Мариотта для политропного процесса можем записать . Откуда(5.6)

Из уравнения состояния идеального газа получим .

Подставляя это значение в уравнение (5.6) , получим

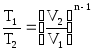(5.7)

После несложных преобразований из уравнений (5.6) и (5.7) определяем

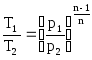(5.8)

Работа в политропном процессе

Для получения уравнения, характеризующего работу в политропном процессе, воспользуемся выражениями для полной работы процесса A=и уравнением политропы.Из последнего выражения выразим текущее значение давления. Подставив это выражение для давления в формулу для работы ,получим

Если ввести ещё одну характеристику политропного процессаa=DU/Q, то, не производя расчета, только на основании значения показателя политропы n можно определить в каком соотношении находятся между собой Q,aиDU.

Используя выражение для n () , произведя несложные преобразования, получим. Откуда, где k = C_p / C_{v .} Тогдаa=DU / Q =

Пример: рассчитать доли затрат подведенной к системе теплоты на изменение внутренней энергии и на совершение работы для показателя политропы n = 0,8 и двухатомного газа ( k = 1,4). Величина коэффициента aa= -0,2 / -0,6 = 1/3. Таким образом,DU = 1/3 Q , а А = 2/3 Q, т. е. 1/3 подведенной теплоты затрачивается на изменение внутренней энергии , а 2/3 - на совершение работы.

Круговые термодинамические процессы (циклы)

Тепловой двигатель, в котором теплота сколь угодно долго превращалась бы в работу, не может работать по разомкнутому процессу. Действительно, теплота должна подводиться от какого-то источника с заданной температурой Т_{ист .}Если процесс расширения осуществляется при p = Const , то температура рабочего тела будет возрастать до тех пор, пока её величина не станет равной температуре источника. Если в цилиндре двигателя газ расширяется при постоянной температуре, то давление в нем будет уменьшаться. И как только оно станет равным давлению в окружающей среде - двигатель остановится. В связи с этим рабочее тело (например, газ)в тепловом двигателе осуществляет круговой процесс (цикл) , возвращаясь каждый раз в исходное состояние рис. 5.4. При подводе к газу (от источника) теплоты в количестве Q_под происходит процесс расширения по политропе 1-а-2 и газ производит работу А_расш, равную площади 1-а-2-с-d-1 . При этом энтропия рабочего тела возрастает. В обратном процессе 2-в-1 восстанавливаются прежние значения координат состояния - S и V (соответственно восстанавливаются значения потенциалов Т и р). При сжатии газа до первоначального объема от него отводится теплота в количестве Q_отв, а энтропия уменьшается до начального значения. Работа , затраченная на сжатие газа А_сж, в p-V координатах определяется площадью 2-в-1-d-c-2. Таким образом, полезная работа за цикл А_полравна разности работ расширения и сжатия и изобразится площадью, заключенной внутри цикла

А_пол= А_расш- А_сж (5.10)

Цикл тепловой машины в T-S координатах представлен на рис.5.5. Здесь Q_под определяется площадью 1-а-2-в-с-d-1, Q_{отв -} площадью 2-в-1-d-c-2. Количество теплоты, преобразованной в работу, изобразится площадью, заключенной внутри цикла.

Аналогичные результаты можно получить , используя первый закон термодинамики для процессов расширения (Q_под =DU_1-a-2 + A_расш) и сжатия (- Q_отв=DU_2-b-1- A_сж ). При отводе теплоты и сжатии газа теплота и работа отрицательные (поставлен знак минус). Суммируя эти уравнения и учитывая, что внутренняя энергия, как функция состояния, не изменяется в цикле, (DU_1-а-2=DU_2-b-1) запишем

Q_под- Q_отв= А_расш- А_сж= А_под (5.11)

Эффективность работы теплового двигателя оценивается термическим коэффициентом полезного действия

(5.12)

В уравнение (5.12) значение Q_отвподставляется по абсолютной величине, так как знак (минус) при Q_отвбыл учтен ранее.

Особенности циклов тепловых машин

1. Линия расширения лежит выше линии сжатия.

2. Теплота подводится при высокой температуре, а отводится при более низкой температуре. Таким образом, в тепловом двигателе происходит перенос теплоты с верхнего температурного уровня на нижний температурный уровень.

Все процессы в цикле равновесные. Для того, чтобы подвести или отвести от рабочего тела теплоту равновесным образом при переменной его температуре необходимо иметь бесконечно большое количество источников теплоты и холодильников, еак как в каждый данный момент разность температур источника и рабочего тела, а также рабочего тела и холодильника должна быть бесконечно малой.

Цикл Карно

Цикл, дающий максимальное значение термического к.п.д. (при определенных температурах нагревателя и охладителя), предложенный французским ученым-инженером Сади Карно, носит название цикла Карно.

Цикл Карно, состоящий из двух изотермических и двух адиабатных процессов и изображенный в различных координатах, представлен на рис. 5.6 (в координатах p-V - рис 5.6,а , в координатах T-S - на рис. 5.6,б). Процессы считаются равновесными, поэтому подвод теплоты к рабочему телу в изотермическом процессе 1-2 осуществляется от теплового источника, температура которого выше температуры рабочего тела на бесконечно малую величину (Т_ист= T₁+ dT). Понижение температуры рабочего тела от Т₁до Т₂осуществляется в процессе 2-3 при равновесном адиабатном расширении газа. Для уменьшения энтропии рабочего тела до первоначального значения от него в процессе 3-4 отводится теплота в холодильник, температура которого на бесконечно малую величину меньше температуры рабочего тела Т₂. Цикл замыкается адиабатным сжатием в процессе 4-1.

Термический к.п.д. цикла Карно в соответствии с уравнением (5.12) определяется

следующим образом:

Так как DS_1-2 = êDS_3-4 ê, то (5.13)

Теорема Карно

Теорема формулируется следующим образом. Термический КПД цикла Карно не зависит от физических свойств рабочего тела и имеет максимальное значение из всех возможных циклов в заданном интервале температур. Первая часть теоремы не требует доказательства, так как в выражение для не входят физические константы рабочего тела. Значениезависит только от разности температур, при которых подводится и отводится теплота в цикле. На рис 5.7 изображен цикл Карно 1-2-3-4 и вписанный в него произвольный цикл АBCD .

Для доказательства второй части теоремы Карно разобьем диаграмму цикла множеством адиабат и рассмотрим какой-либо из полученных элементарных циклов, например, efgh. В более крупном масштабе последний изображен на рис.5.7б. Этот цикл состоит из двух адиабат и двух политроп ef и gf. 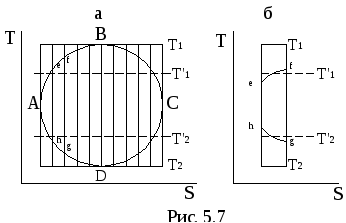При бесконечно большом числе элементарных циклов изменение температуры в политропных процессах ef и gh будет бесконечно малым, поэтому указанные политропы можно будет заменить изотермами с температурамии. Тогда термический КПД цикла efgh можно рассчитать по формуле (5.13)

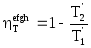, а

Так как >, а Т₂ <, то<. Аналогичный вывод можно сделать по отношению к каждому из элементарных циклов. Поэтому данный вывод справедлив и для цикла ABCD , т.е.<.

Полученный результат объясняется тем, что термический КПД любого цикла зависит не от максимальной разности температур, достигаемой в цикле, а зависит от средне интегральных температур, при которых подводится и отводится теплота в цикле. В цикле АBCD теплота подводится от точки А до точки С при средне интегральной температуре , а отводится - при средне интегральной температуре . Следовательно, эффективная разность температур в цикле АВСD меньше разности температур в цикле Карно, поэтому<.

Несмотря на то, что в цикле Карно теплота наиболее эффективно преобразуется в работу, этот цикл в реальных тепловых двигателях не применяется по следующим причинам:

1. Если цикл Карно в p-V координатах изобразить в масштабе, то то окажется, что полезная работа за цикл будет очень незначительной (рис. 5.8). Для того чтобы от машины получить большую мощность, она должна совершать большое число циклов в единицу времени, т. е. должна быть быстроходной. У быстроходной машины будет низкий механический КПД и выигрыш в термическом КПД не компенсирует проигрыш в механическом КПД.

2. В цилиндре двигателя, работающего по циклу Карно, будут развиваться очень высокие давления. Рассмотрим это на примере двигателя внутреннего сгорания, работающего по адиабатическому процессу:

или

В двигателях внутреннего сгорания подводится при температуре сгорания топлива Т₁ @1800 К, а отводится в атмосферу при Т₄@300 К и давлении р₁= = 0,1 МПа. Приняв величину k = 1,35 , получим значение р₄= 120 Мпа.

Несмотря на указанные причины цикл Карно имеет большое значение, так как служит эталоном при проектировании реальных двигателей.

Некоторые общие сведения о циклах холодильных машин

Цикл холодильной машины в p-V и T-S координатах изображен на рис. 5.9 и 5.10.

В холодильной машине теплота подводится к рабочему телу (хладагенту) от охлаждаемого тела, например, от охлаждаемых продуктов, находящихся в холодильной камере. в которой поддерживается минусовая температура. Теплота от рабочего тела отводится при более высокой температуре. Перенос теплоты от нижнего температурного уровня на верхний в холодильной машине оказывается возможным благодаря работе, затрачиваемой на проведение цикла. Эффективность работы холодильной машины оценивается значением холодильного коэффициента

e=Q_под/ A_затр ,

представляющий собой отношение хладопроизводительности машины хладопроизводительность машины (Q_под) к затраченной работе.

Для примера на рис 5.11 и 5.12 приведены принципиальная схема и цикл воздушно-комперессионной холодильной машины. И теплообменника охлаждаемой камеры 1 воздух засасывается компрессором, в котором адиабатически сжимается, в результате чего температура его повышается с Т₁ до Т₂. В холодильнике 3 воздух при давлении р₂охлаждается до температуры Т₃. Из холодильника воздух направляется в расширительную машину (детандер) 4, в которой при адиабатическом расширении его температура понижается до Т₄ . В холодильной камере воздух отбирает теплоту от охлаждаемых продуктов и нагревается до температуры Т₁