Глава 14. Тепловая теорема Нернса (постулат Нернста). Абсолютное значение энтропии. Свойства веществ вблизи абсолютного нуля температуры

Особенность энтропии состоит, в частности, в том, что она введена в науку через свой дифференциал, а не по абсолютному значению, как все другие координаты состояния. Определить абсолютное значение энтропии, опираясь только на первый и второй законы термодинамики, не представляется возможным, так как при этом возникают непреодолимые трудности при выборе константы интегрирования, т.е. при определении нуля отсчета энтропии. Между тем, в термодинамике широко используются функции, дифференциал которых содержит абсолютное значение энтропии, например свободная энергия и свободная энтальпия

dF = SdT - pdV и dФ = SdT +Vdp

Трудности в определении абсолютного значения энтропии были преодолены Нернстом (1906 г.). Постулат Нернста по праву называют третьим законом термодинамики, так как он содержит результаты, которые не нашли отражения в первых двух законах. Анализируя многочисленные опытные данные , накопленные при изучении поведения веществ при низких температурах, Нернст пришел к выводу, что при химических реакциях, протекающих в изохорно-изотермических условиях, разность между изменениями свободной энергии DF и внутренней энергиейDU (DF-DU) весьма мала. С понижением температуры тела эта разность уменьшается. Когда температура устремляется к нулю Кельвина значенияDF иDUасимптотически приближаются друг к другу и при Т = 0 К DF = DU. Действительно,

F = U - TS (14.1)

Запишем это уравнение для двух состояний в рассматриваемых условиях

F₁ = U₁ - TS₁ и F₂ = U₂ - TS_2. Вычитая одно из другого, получимDF = DU - TDS

При Т = 0 К DF = DU. Из соотношения дляdF приV =Constследует. Подставляя это значение S в (14.1), получим

или (14.2)

В изобарно-изотермических условиях характеристической функцией является свободная энтальпия

Ф = U -TS +pV = I -TS (14.3)

и dФ = - SdT +Vdp. Приp = Const . Подставляя это значениеSв уравнение (14.3), находим Ф =I + Tили

DФ =DI + T (14.4)

Уравнения (14.2) и (14.4) называются уравнениями Гиббса-Гельмгольца. Эти уравнения можно записать в виде

(14.5)

Основываясь на большом опытном материале, накопленном к тому времени при изучении свойств тел вблизи абсолютного нуля температуры, Нернст предположил, что уменьшение значений разностей (DF - DU) и(DФ -DI)вблизи абсолютного нуля является следствием понижения не только самой температуры, но и значений производныхи .

Следовательно, = = 0

Аналогично = = 0 (14.6)

Эти уравнения в математической форме выражают постулат Ненрнста. Таким образом, установлено, что существует некоторый интервал температур, в пределах которого изменение свободной энергии в ходе изохорно-изотермической реакции, а также изменение свободной энтальпии и энтальпии в ходе изобарно-изотермической реакции различаются незначительно.

Абсолютное значение энтропии

Уравнения (18.6) можно представить в другом виде. Учитывая, что

, из (18.6) получим

lim _{T® 0}(S₂ - S₁) = lim _{T® 0}DS = 0 (14.7)

Это значит , что вблизи абсолютного нуля температуры в изотермическом процессе энтропия не меняется и принимает некоторое предельное значение S₀.

М. Планк развил дальше теорию Нернста. Он показал, что предельное значение энтропии для всех тел одинаково и не может быть ни чем иным, как абсолютным нулем энтропии, т.е. S₀ = 0, или

lim _{T® 0}DS = 0 (14.8)

Свойства тел вблизи абсолютного нуля температуры

Термические коэффициентыИзвестно, что производныеиназываются термической расширяемостью и термической упругостью соответственно. Величиныиназываются коэффициентами термической расширяемости и термической упругости. При приближении к абсолютному нулюdF = - SdT - pdV иdФ = -SdT + Vdp. Из этих выражений для дифференциала свободной энергии и свободной энтальпии мы получили два дифференциальных соотношения -

и. Следовательно,

. По теореме Нернста, при Т®0 энтропия не меняется (dS = 0), поэтому при Т®0

b_V ® 0 иb_р®0 (14.9)

Энтропия и теплоемкости С_p и С_V

Воспользуемся полученными ранее соотношениями и.

Интегрируя, получим

и (14.10)

Из уравнения (14.10) следует, что при Т ®0 теплоёмкости С_V и С_рдолжны устремляться к нулю. Другой результат противоречил бы теореме Нернста.. Действительно, если принять, что вблизи абсолютного нуля теплоёмкость будет иметь конечное значение, например, при её зависимости от температуры вида С_V = a + bT + ... ,то подставив это значение С_V в (14.10)

получим = (14.11)

Из уравнения (14.11) следует, что при любой температуре, отличной от нуля

S ® - ¥ . Это противоречит теореме Нернста, в соответствии с которой энтропия должна иметь конечное значение.

Из уравнения (14.10) следует , что для расчета абсолютного значения энтропии нужно только знать зависимость теплоемкостей С_V и С_рот температуры и термическое уравнение состояния.

Недостижимость абсолютного нуля температуры

На рис. 14.2 изображен цикл Карно, в котором теплота подводится при тнмператауре Т₁, а отводится при температуре Т₂= 0 К. Очевидно , что в цикле SDS= 0, т.е.

DS_1-2 + DS_2-3 + DS_3-4+ DS_4-1 = 0 (14.12)

Так как процессы 2-3 и 4-1 адиабатные , то DS_2-3 = DS_4-1=0. В соответствии с теоремой НернстаDS_3-4= 0. Следовательно первое слагаемое в левой части уравнения (14.2) также равно нулю DS_1-2 =Q/T = 0, хотя Q ¹ 0 и Т₁¹ ¹ ¥. Далее, в процессе 3-4 энтропия изменяется, в то время как в соответствии с теоремой Нернстаона должна оставаться постоянной величиной, так как Т₂= 0 К. Эти противоречия указывают на то,что понизить температуру до абсолютного нуля невозможно.

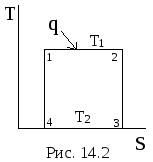
Отвод теплоты от рабочего тела при температуре Т ®0 К невозможен и потому, что теплоёмкость вещества устремляется к нулю быстрее, чем сама температура. При некоторой температуре, большей абсолютного нуля, теплоемкость может оказаться равной нулю.