
Математический анализ II Учебное Пособие
.pdfМинистерство образования Российской Федерации
Санкт-Петербургский государственный институт точной механики и оптики
(технический университет)
Математический анализ II
Санкт-Петербург
2002
Министерство образования Российской Федерации
Санкт-Петербургский государственный институт точной механики и оптики
(технический университет)
Кафедра высшей математики
Математический анализ II
Учебное пособие
Под общей редакцией Л.С. Ратафьевой
Санкт-Петербург
2002
© Санкт-Петербургский государственный институт точной механики и оптики
Коллектив авторов:
И.А. Лапин, Л.С. Ратафьева
Математический анализ II /Под общей редакцией Л.С. Ратафьевой/ Учебное пособие. СПб: СпбГИТМО (ТУ). 2002. …с.
Предлагаемое учебное пособие представляет собой базовый конспект лекций по высшей математике для студентов 1 курса (II семестр) дневного и вечернего отделения общеинженерных специальностей. В нём рассмотрены следующие темы: 1. Определённые интегралы. 2. Несобственные интегралы. 3. Двойные и тройные интегралы. 4. Криволинейные интегралы. 5. Поверхностные интегралы. 6. Элементы теории поля. Содержание пособия соответствует федеральным образовательным стандартам и программе дисциплины "математика" для направления 550000 - Технические науки. 2000 г. Основное назначение пособия - помочь студентам в самостоятельном изучении данных разделов курса в условиях сокращённого количества аудиторных занятий. Является вторым изданием учебных пособий Анализ I и Математические основы теории физических полей, изданных в ЛИТМО в 1991 г. и в 1989 г. соответственно.
Содержание учебного пособия разбито на главы, параграфы и пункты. Нумерация формул, теорем, примеров и рисунков сделаны по параграфам.
Список использованной литературы приводится в конце пособия без дополнительных ссылок.
Одобрено на заседании кафедры высшей математики ИТМО (ТУ)
(протокол №3 от 8.02.2000 г.)
3
ОГЛАВЛЕНИЕ |
|
Глава I. Определённый интеграл........................................... |
|
§1. Определённый интеграл. Его свойства............................................ |
5 |
§2. Вычисление определённого интеграла............................................ |
10 |
§3. Приложения определённого интеграла............................................ |
15 |
§4. Общая схема применения определённого интеграла..................... |
22 |
Глава II. Несобственные интегралы...................................... |
|
§1. Несобственные интегралы по неограниченному промежутку...... |
|
§2. Несобственные интегралы от неограниченных функций.............. |
|
§3. Интегралы, зависящие от параметра................................................ |
|
§4. Гамма - функция................................................................................. |
|
§5. Бета - функция.................................................................................... |
|
Глава III. Двойной и тройной интегралы............................. |
|
§1. Двойной интеграл............................................................................... |
|
§2. Тройной интеграл............................................................................... |
|
§3. Применения двойных и тройных интегралов.................................. |
|
§4. Криволинейные координаты и замена переменных в кратных |
|
интегралах................................................................................................ |
|
Глава IV. Криволинейные интегралы.................................. |
|
§1. Криволинейные интегралы I рода.................................................... |
|
§2. Криволинейные интегралы II рода................................................... |
|
§3. Формула Грина................................................................................... |
|
§4. Криволинейные интегралы, не зависящие от пути |
|
интегрирования......................................................................................... |
|
Глава V. Поверхностные интегралы...................................... |
|
§1. Поверхностные интегралы I рода..................................................... |
|
§2. Поверхностные интегралы II рода.................................................... |
|
§3. Формула Остроградского.................................................................. |
|
§4. Формула Стокса.................................................................................. |
|
Глава VI. Элементы теории поля ........................................... |
|
§1. Скалярное поле. Градиент. Производная по направлению ........... |
|
§2. Векторное поле................................................................................... |
|
3
§3. Теорема Остроградского (векторная форма). Дивергенция
векторного поля и её механический смысл...........................................
§4. Скалярное векторное поле и его свойства. Уравнение
неразрывности . Оператор Лапласа........................................................
§5. Циркуляция векторного поля по замкнутому контуру. Вихрь
векторного поля. Векторная форма теоремы Стокса ...........................
§6. Потенциальное векторное поле ........................................................
Приложение 1. Интеграл Лебега............................................
Приложение 2. Интеграл Стилитьеса...................................
4
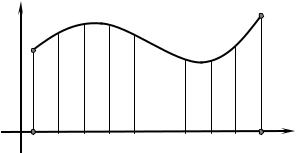
ГЛАВА I. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
§1. Определённый интеграл. Его свойства
1. Определение определённого интеграла
y |
|
|
|
B |
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим некоторую |
|||
|
|
|
|
||||
|
|
|
|
|
|||
|
|
|
|
|
функцию |
y = f (x ) , |
опре- |
|
|
|
|
|
делённую |
на промежутке |
|
D |
|
|
|
C |
[a ;b] (a <b) , рис 1. |
|
|
0 a |
x |
|
|
b x |
|
|
|
k ξ x |
k +1 |
|
|
|
|||
|
|
k |
|
|
|
|
|
|
|
Рис 1 |
|
|
|
|
|
Выполним 5 операций. |
|
|
|
|
|||
1. Разобьём промежуток [a ;b] точками x 0 =a ,x1 ,x 2 ,...,xk ,xk +1,...,xn =b |
|||||||
произвольным образом на n |
частей. |
Обозначим xk =xk +1 −xk , |
а наи- |
||||
большую |
из длин этих частичных участков обозначим через |
λ , т.е. |
|||||
λ= sup{ xk }; λ будем называть рангом дробления.
2.На каждом частичном участке [xk , xk +1 ] возьмём произвольную точку ξk
ивычислим в ней значение функции f (ξk ) .
3.Составим произведение f (ξk ) xk
4.Составим сумму
n −1
σn = ∑f (ξk ) xk k =0
Эта сумма называется интегральной суммой или суммой Римана.
5.Измельчая дробление (за счёт увеличения числа точек дробления n ) и устремляя при этом ранг дробления к нулю (λ → 0) т.е. (увеличивая чис-
ло точек дробления, мы следим за тем, чтобы уменьшалась и стремилась к нулю длина всех частичных участков xk ), будем находить предел по-
следовательности интегральных сумм
J = limσn
n →∞
λ→0
5
Если этот предел существует, не зависит от способа дробления и выбора точек ξk , то он называется определённым интегралом от функции f (x ) по
промежутку [a ,b] и обозначается так:
J = ∫b f (x )dx
a
Итак, мы привели ни что иное, как развёрнутое определение определённого интеграла от функции f (x ) по промежутку [a ,b]. Принимая во внима-
ние сказанное выше, можем дать определение определённого интеграла более компактно так:
b |
def |
n −1 |
∫f (x )dx = nlim→∞ |
∑f (ξk ) xk (a <b) , |
|
a |
λ→0 |
k =0 |
где a -нижний предел интегрирования, b - верхний предел. В этом случае,
когда для функции f (x ) существует определённый интеграл ∫b f (x )dx ,
a
функция f (x ) называется интегрируемой на промежутке [a ,b]. Заметим,
что в приведённом определении предполагается, что a <b . Понятие определённого интеграла можно обобщить и на случай, когда b <a или b =a . Действительно, будем считать по определению, что
если b <a , то ∫b |
f (x )dx = −a∫f (x )dx , а если a =b , то ∫b f (x )dx = 0 |
|
a |
b |
a |
2. Теорема существования определённого интеграла
Возникает вопрос: всякая ли функция f (x ) интегрируема на данном промежутке [a ,b]. Предварительно дадим определение кусочнонепрерывной функции.
Определение. Функция f (x ) называется кусочно-непрерывной на данном промежутке [a ,b], если на этом промежутке она ограничена и имеет
лишь конечное число точек разрыва.
Геометрически кусочно-непрерывную функцию можно изобразить линией, состоящей из конечного числа непрерывных участков. Очевидно, что функция, непрерывная на промежутке [a ,b], является частным случаем ку- сочно-непрерывной функции.
Приведём теперь без доказательства теорему существования определённого интеграла.
6
Теорема (достаточное условие интегрируемости). Если функ-
ция f (x ) кусочно-непрерывна на промежутке [a ,b], то на этом проме-
жутке она интегрируема, т.е. существует ∫b f (x )dx .
a
Заметим, что класс функций, указанных в теореме, практически исчерпывает все функции, встречающиеся в приложениях. В дальнейшем мы будем предполагать, что рассматриваются только такие функции.
3. Геометрический смысл определённого интеграла
Допустим, что функция f (x ) непрерывна и положительна на промежутке [a ,b]. Рассмотрим криволинейную трапецию A B C D (рис 1). Интегральная
n −1
сумма σn = ∑f (ξk ) xk даёт нам сумму площадей прямоугольников с ос-
k =0
нованиями xk и высотами f (ξk ) . Её можно принять за приближённое зна-
чение площади криволинейной трапеции A B C D , т.е.
n −1
SA B C D ≈ ∑f (ξk ) xk , k =0
причём, это равенство будет тем точнее, чем мельче дробление, и в пределе при n → +∞ и λ → 0 мы получим
SA B C D = ∫b f (x )dx
a
Вэтом и заключается геометрический смысл определённого интеграла.
4.Свойства определённого интеграла
Свойство 1. a∫f (x )dx = 0 (по определению)
a
Свойство 2. ∫b f (x )dx = −a∫f (x )dx (по определению), т.е. при перемене
a |
b |
местами пределов интегрирования определённый интеграл меняет знак на противоположный.
Свойство 3.(линейность интеграла)
∫b [c1f1(x ) +c 2 f2 (x )]dx =c1 ∫b f1(x )dx +c 2 ∫b f2 (x )dx
a a a
Для доказательства достаточно составить интегральную сумму для функции y =c1f1(x ) +c 2 f2 (x ) и воспользоваться свойствами пределов функ-
ции. Действительно,
7

|
n −1 |
|
n −1 |
|
n −1 |
nlim→∞ |
∑[c1f1(ξk ) +c 2 f2 (ξ2 )] |
xk =c1 nlim→∞ |
∑f1(ξk ) |
xk +c 2 nlim→∞ |
∑f2 (ξk ) xk = |
λ→0 |
k =0 |
λ→0 |
k =0 |
λ→0 |
k =0 |
=c1 ∫b f1(x )dx |
+ c 2 ∫b f2 (x )dx |
a |
a |
Отметим, что из доказанного свойства следуют такие очевидные факты а) ∫b cf (x )dx =c ∫b f (x )dx ,
a a
т.е. постоянный множитель можно выносить за знак определённого интеграла
б) ∫b [f1(x ) + f2 (x )]= ∫b f1(x )dx + ∫b f2 (x )dx ,
a |
a |
a |
т.е. интеграл от суммы функций равен сумме интегралов от этих функций по данному промежутку [a ,b].
Свойство 4. Каковы бы ни были числа |
y |
A |
C |
B |
||
b |
c |
b |
|
|||
a ,b,c , ∫f (x )dx = ∫f (x )dx + ∫f (x )dx , |
|
|
|
|
||
a |
a |
c |
|
|
|
|
лишь бы только функция f (x ) была |
|
|
|
|
||
бы интегрируема на каждом из |
|
|
|
b x |
||
промежутков [a ,b],[a ,c ] и [c ,b] (рис 2). |
0 a |
c |
||||
рис 2
Для доказательства этого свойства достаточно составить интегральные суммы для каждого из трёх интегралов, включив точку c в число точек деления, а затем рассмотреть пределы получившихся интегральных сумм при условии, что n → ∞, λ → 0 .
Свойство 5. (Теорема. Оценка определённого интеграла)
Теорема. Если f (x ) непрерывна на промежутке [a ,b], то имеет место такая оценка определённого интеграла:
m (b −a ) ≤ ∫b f (x )dx ≤M (b −a ) ,
a
где m -наименьшее, а M - наибольшее значения функции f (x ) на промежутке [a ,b].
Доказательство. Очевидно, что функция f (x ) имеет на промежутке [a ,b] наименьшее (m ) и наибольшее (M ) значения, т.к. f (x ) непрерывна на промежутке [a ,b], т.е.
x [a ,b] :m ≤ f (x ) ≤M .
8

|
|
n −1 |
Составим интегральную сумму для f (x ) : σn = ∑f (ξk ) xk . Ясно, что |
||
|
|
k =0 |
n −1 |
n −1 |
n −1 |
∑m |
xk ≤ ∑f (ξk ) |
xk ≤ ∑M xk . |
k =0 |
k =0 |
k =0 |
n −1
Учитывая, что ∑ xk =b −a и, вынося постоянный множитель за знак
k =0
суммы, получим:
n −1
m (b −a ) ≤ ∑f (ξk ) xk ≤M (b −a )
k =0
Измельчая дробление и устремляя ранг дробления к нулю, в пределе получим
m (b −a ) ≤ ∫b f (x )dx ≤M (b −a ) .
a
Свойство 6. (Теорема о среднем)
Теорема. Если f (x ) непрерывна на промежутке [a ,b], то между точками a и b найдётся хотя бы одна точка ξ такая, что будет иметь место равенство
∫b f (x )dx = f (ξ) (b −a )
a
Доказательство. Допустим, что a <b . В силу свойства 4 имеет место оценка
m (b −a ) ≤ ∫b f (x )dx ≤M (b −a ) .
a
Функция f (x ) непрерывна на промежутке [a ,b], следовательно, прини-
мая значения, равные m и M , она принимает и всякое промежуточное значение, т.е. найдётся точка ξ (a <ξ <b) такая, что функция f (x ) примет в
этой точке значение равное |
1 |
∫b f (x )dx , т.е. будет |
||
|
|
|||
|
|
b −a a |
||
f (ξ) = |
1 |
∫b f (x )dx => ∫b f (x )dx = f (ξ) (b −a ) . |
||
|
||||
|
b −a a |
a |
||
M
y
m |
|
|
0 a |
ξ |
b x |
|
Рис 3 |
|
Заметим, что значения функции f (x ) в точке ξ : f (ξ) называется
"средним", откуда и название этого свойства.
9
