43. Понятие о доверительных оценках и доверительном интервале

Точечная оценка параметра распределения полученная по данным одновр выборки не содержит никаких суждений относительно истинности значений исслед параметра.

Для получения более полной оценки огр-ся интервал, в котором с заданной надежностью (r ) будет находиться истинное значение параметра ɵ, такой интервал называется доверительным интервалом параметров распределения.

r = 0,9; 0,95; 0,99

Оценка параметра распределения на основе доверительного интервала называется интервальной оценкой.

Величина доверительного интервала зависит:

1. от объема выборки

2. от значения доверительной вероятности r.

С ростом объема выборки доверительный интервал сужается, т.е явл более точным.

С ростом доверительной вероятности доверительный интервал расширяется, становится менее надежным.

44. Доверительная оценка неизвестной вероятности (npq>=10)

При этом условии частота события имеет закон распределения близкий к нормальному.

Рассмотрим сл.вел 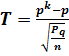, которая распределена по закону Гаусса при заданной надежности r по таблице значений ф-ий Лапласа определяется критическое значение распред Гаусса (+2), для кот выписывается ее равенство.

=>↔

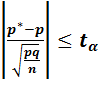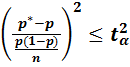
(1)

Из решения неравенства (1) опред границы довер-го интервала неизвестной вероятности.

Графики границы доверительного интервала при фиксированном ta можно определить как точки пересечения прямой х=р* и так называемого эллипса доверия, кот.описывается в уравнении (1).

Эллипс доверия сужается с ростом объема выборки и при уменьшении надежности r.

Чем точнее оценка, тем менее она надежна, чем надежнее оценка , тем менее она точна, при фиксированной надежности, точность оценки можно повысить за счет увеличения объема выборки.

45. Доверительная оценка неизвестной вероятности (npq<10)

npq<10 => m/n; р,

0, 1/n, 2/n, … 1

Вероятность возможн знач.

Пусть к- число испытаний, в котором событие наступило. к= p*n

Границы доверительного интервала неизвестной вероятности опред из уравнения

р1:

р2:

рассм.сл.,когда

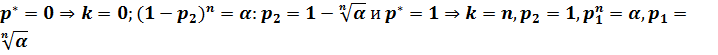
46. Доверительная оценка при неизвестном м и неизвестном d

Дана выборка предположительно отобранная из нормального распределения генеральной совокупности, параметры которого нам неизвестны.

По выбор. дан. полученной оценки Н.З.Р

Рассмотрим СВ

СВ Т распределяется по закону Стьюдента с (n-1) степенями свободы..

Число степеней свободы определяется как общее число, как общее число наблюд признаков х к числу уравнений связывающих эти наблюдения.

При заданной надежности Ɣ и по числу степени n-1 определяет критическое значение распределения Гаусса.⇒

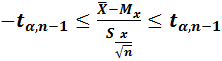
При n≥30 распр.Стъюдента практически совпадает с распр.Гаусса и дов.инт.неизв.мат.ож.опред.по форме:

47. Доверительная оценка неизвестной Dx при неизвестном Mx

Существуют два основных метода построения доверительных интервалов: байесовский метод и метод доверительных интервалов, предложенный Нейманом. Применяя метод построения доверительных интервалов, основанный на формуле Байеса, исходят из предположения, что оцениваемый параметр сам случаен. Предполагается также, что известно априорное распределение параметра. Этот метод часто неприменим, так как оцениваемая величина на практике является просто неизвестной постоянной, а не случайной величиной. Кроме того, ее распределение бывает также неизвестным. От этих недостатков свободен метод доверительных интервалов.

Найдем доверительный интервал для дисперсии D[X]=σ² нормально распределенного признака Х с неизвестным математическим ожиданием. При выводе интервальной оценки, в случае известного математического ожидания, мы пользовались

_k

величиной Ḋ_B=(1\n)*∑ *n_i*(x_i-α)². Теперь это значение

ⁱ⁼¹

использовать нельзя, поэтому в качестве несмещенной оценки дисперсии будем использовать исправленную выборочную дисперсию S²=(n\n-1)* Ḋ_B . Случайная величина

Z_n-1=(n-1)S²)\σ² имеет распределение Пирсона χ² с (n-1) степенями свободы. Выберем близкую к единице вероятность γ и найдем интервал, в который попадает неизвестный параметр с надежностью γ . Получим, что оцениваемое значение дисперсии D[X]=σ² с надежностью γ покрывается доверительным интервалом

((n-1)S²)\h₂ ; (n-1)S²)\h₁ ).