§2. Теорема Гаусса

I. Краткие теоретические сведения

Теорема Гаусса: поток векторасквозь замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на.

.

Число задач, легко решаемых с помощью теоремы Гаусса, ограничено. Применять теорему Гаусса эффективно лишь в том случае, когда поле обладает специфической симметрией – плоской, сферической или цилиндрической. В этом случае легко найти достаточно простую замкнутую гауссову поверхность.

Для упрощения математических расчетов во многих случаях истинное распределение точечных дискретных зарядов заменяют непрерывным распределением с некоторой объемной , поверхностнойили линейнойплотностью.

Объемная плотность заряда:

.

Поверхностная плотность заряда:

.

Линейная плотность заряда:

.

II. Примеры решения задач

Пример 2.1.Найти поле равномерно заряженного по объему зарядовой плотностьюбесконечного цилиндра на расстоянииrот его оси. Радиус цилиндраR.

Решение.

Электростатическое поле равномерно заряженного цилиндра имеет радиальный характер: направление вектора Eв любой точке перпендикулярно оси цилиндра, а модуль вектораEзависит только от расстоянияrдо оси цилиндра. (рис.2.1.). Ясно, что при такой конфигурации поля в качестве гауссовой поверхности нужно взять цилиндр радиусаr, ось которого совпадает с осью данного цилиндра (рис. 2.2.). Тогда модуль вектораEна гауссовой поверхности всюду имеет одинаковое значение (данный факт позволяет вынести Eза знак интеграла).

Рассмотрим два случая:

1) Если r<R, то поток вектораE сквозь боковую поверхность гауссова цилиндра примет вид:

,

где- площадь боковой поверхности гауссова цилиндра высотойh.

Заряд, заключенный внутри гауссовой поверхности, равен:

где V- объем цилиндра, в котором сосредоточен заряд. В данном случаеVсовпадает с объемом гауссова цилиндра.

.

2) При r>R

.

Теперь Vне совпадает с объемом гауссова цилиндра

.

Тогда :

.

Пример 2.2.Бесконечно длинный цилиндр радиусаRзаряжен с объемной плотностью,a- постоянная,r- расстояние от оси цилиндра. НайтиE(r).

Решение.

Все рассуждения относительно выбора гауссовой поверхности повторяют предыдущую задачу. Поэтому сразу перейдем к рассмотрению двух случаев.

1. При r<Rи. Так как объемная плотность является функцией расстоянияr, тонельзя выносить за знак интеграла, как это делалось ранее.

.

Тогда

.

2) При r>R

.

Следует обратить внимание, что интегрирование идет в пределах от 0 до R. В пространстве отRдоrзаряда нет.

Пример 2.3.На оси бесконечно длинного полого цилиндра радиусаRрасположена бесконечная нить, заряженная с линейной плотностью. Пространство за цилиндром заряжено с объемной плотностью,₀- постоянная,r- расстояние от оси цилиндра. НайтиE(r).

Решение.

Поле обладает цилиндрической симметрией, поэтому выбор гауссовой поверхности очевиден.

1) При r<Rсуществует только электростатическое поле, созданное нитью

.

Заряд:

2) При r>Rв области существует как поле нити, так и поле, создаваемое заряженной средой. В силу принципа суперпозиции:

.

Заметим, что поле среды также обладает цилиндрической симметрией, поэтому от векторов в принципе суперпозиции можно перейти к модулям:

.

Определим поле среды:

При поле, создаваемое нитью, стремится к нулю; поле же среды с расстоянием растет, что связано с возрастающей от расстояния объемной плотностью заряда.

Пример 5.4.Внутри бесконечно длинного равномерно заряженного цилиндра имеется бесконечная цилиндрическая полость (Рис.2.3). Объемная плотность заряда цилиндра. Ось цилиндрической полости параллельна оси цилиндра и смещена относительно нее на расстояние, характеризуемое вектором. НайтиEвнутри полости.

Решение.

При решении данной задачи пользуются модельным представлением: вместо цилиндра с полостью рассматривают равномерно заряженный (для определенности пусть ) большой цилиндр и отрицательно заряженный сцилиндр меньшего радиуса в нем. Такая модель соответствует исходной постановке задачи, так как в области полости отрицательные и положительные заряды компенсируют друг друга, и позволяет использовать принцип суперпозиции, что значительно упрощает решение задачи.

Определим напряженность поля большого цилиндра в точке, характеризуемой радиус-вектором (рис. 2.4):

Аналогично, . В векторной форме общее поле внутри полости имеет вид:

.

Знак «-» появился из-за того, что цилиндр меньшего диаметра заряжен отрицательно.

.

Таким, образом, поле в полости является однородным, и вектор направлен параллельно вектору. Этот вывод справедлив независимо от соотношения радиусов цилиндров и расстояния между их центрами.

Пример 2.5.Две длинные параллельные нити равномерно заряжены каждая с линейной плотностью. Расстояние между нитямиl. Найти максимальное значение модуля напряженности электрического поля в плоскости симметрии этой системы, расположенной между нитями.

Решение.

Модуль вектора напряженности каждой нити легко определить с помощью теоремы Гаусса. Действительно, выбирая в качестве гауссовой поверхности цилиндр, получим:

.

Внекоторой точкеО(рис. 2.5), лежащей в плоскости симметрии данной системы, напряженность общего электростатического поля нитей определим из принципа суперпозиции:

,

или в проекциях на направление вектора :

.

Так как , то

.

Найдем максимальное значение :

.

Пример 2.6. Шар радиусаRимеет положительный заряд, объемная плотность которого зависит только от расстоянияrдо его центра как, где₀- постоянная. Найти: а) модуль напряженности электростатического поля внутри и вне шара как функциюr; б) максимальное значение модуля напряженностии соответствующее ему значение.

Решение.

а) Поле шара является центрально-симметричным: вектор напряженности электростатического поля направлен по радиус-векторуи проходит через центр шара, а модуль векторазависит только от расстояниядо центра шара. В качестве гауссовой поверхности необходимо выбрать концентрическую сферу радиуса . Рассмотрим два случая:

1) При r<Rнайдем поток векторасквозь гауссову сферу.

,

так как .

На гауссовой поверхности , поэтомуEможно вынести за знак интеграла. Следовательно,, где- площадь гауссовой сферы.

Найдем заряд q, заключенный внутри гауссовой поверхности:

, ,

Подставим полученные значения заряда и потока в формулу теоремы Гаусса:

2) При r>R

.

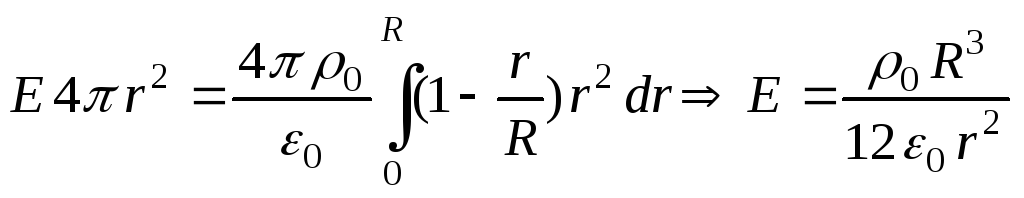б) Найдем максимальное значение модуля напряженности электростатического поля шара . Максимум имеется приr<R, что следует непосредственно из вида зависимостиE(r). Найдем производную:

,

.

Пример 2.7. Вычислить напряженность электростатического поля равномерно заряженной зарядомqсферы радиусаR.

Решение.

В качестве гауссовой поверхности выбираем сферу радиуса r.

1. Пусть r>R. Тогда

2) Пусть r<R. В этом случае замкнутая поверхность не содержит внутри зарядов, поэтому в этой области всюду, т.е. внутри заряженной сферической поверхности электростатическое поле отсутствует.

Пример 2.8.Система состоит из шара радиусаR, заряженного сферически симметрично, и окружающей среды, заполненной зарядом с объемной плотностью, гдеa- постоянная иrрасстояние до центра. Найти заряд шара, при котором модуль напряженности электрического поля вне шара не зависит отr.

Решение.

Так как шар заряжен сферически симметрично, то в качестве гауссовой поверхности выбираем сферу радиуса r.

Пусть искомый заряд шара q. Напряженность электростатического поля приr>Rравна сумме:

.

Тогда .

Напряженность Eне зависит отrпри условии, что.

Пример 2.9.Найти напряженность электрического поля в области пересечения двух шаров, равномерно заполненные разноименными по знаку зарядами с объемной плотностьюи, если расстояние между центрами шаров характеризуется вектором.

Решение.

При решении воспользуемся принципом суперпозиции: , гдеи- напряженности полей, создаваемых шарами с объемными плотностямии, соответственно, в области пересечения (Рис. 2.6). Легко определить, что

, тогда

.

Таким образом, поле внутри области пересечения двух разноименно заряженных шаров однородно, и вектор напряженности параллелен характеристическому вектору.

Пример 2.10.Найти напряженностьполя внутри сферы радиусаR, по которой распределен заряд с поверхностной плотностью, где- постоянная,- полярный угол. При решении использовать тот факт, что такое распределение заряда можно представить как результат малого сдвига друг относительно друга двух равномерно заряженных шаров, заряды которых одинаковы по модулю и противоположны по знаку.

Решение.

Рассмотрим два шара одинакового радиуса R, имеющие равномерно распределенные по объему заряды с плотностьюи. Пусть центры шаров смещены друг относительно друга на вектор(Рис. 2.7). В области пересечения шаров поле является однородным, что было показано в предыдущей задаче:

.

При малом смещении шаров, т. е. при малой длине вектора мы можем перейти к представлению о поверхностной плотности заряда на сфере. Определим толщину заряженного слоя в точках, определяемых углом. Для этого рассмотрим, по теореме косинусов:

,

где R- радиус шара. Так как по условиюR>>a, R>>l

.

При .

Зная толщину слоя и объемную плотность, получаем, что на единицу площади в этом месте приходится заряд , где. Таким образом, мы пришли к выводу, что результат малого сдвига друг относительно друга двух равномерно заряженных шаров приведет к такому же результату, как если бы у нас была сфера с поверхностной плотностью.

Напряженность можно представить как, где- орт осиz, от которой отсчитывается угол.

Пример 2.11.Найти поле плоскости, равномерно заряженной зарядом с поверхностной плотностью.

Решение.

Из симметрии задачи следует, что вектор перпендикулярен плоскости. Он направлен от плоскости, если плоскость заряжена положительно, и к плоскости, если ее заряд отрицателен. В симметричных относительно плоскости точках вектородинаков по модулю. Заметив это, построим гауссову поверхность в виде цилиндра с площадью оснований, расположенными симметрично по разные стороны плоскости. Образующие гауссова цилиндра перпендикулярны плоскости (Рис. 2.8).

Тогда поток вектора напряженности электростатического поля плоскости через одно основание цилиндра будет , а через оба основания. Поток через боковую поверхность равен нулю, т.к.ивзаимно перпендикулярны. Таким образом,. Заряд, содержащийся внутри гауссова цилиндра, равен:. Следовательно,. Т.е. напряженность поля бесконечной равномерно заряженной плоскости не зависит от расстояния до нее.

Пример 2.12.Бесконечно большая пластина толщиной 2dравномерно заряжена с объемной плотностью,₀- постоянная. Осьxперпендикулярна плоскости пластины, начало координат в середине пластины. Найти напряженность электрического поля как функцию расстоянияx.

Решение.

Выберем начало координат в средней плоскости пластинки, а ось xнаправим перпендикулярно к ней (Рис. 2.9). Тогда, проводя рассуждения, как в предыдущей задаче, рассмотрим два случая:

1) При x<d

, ,

где V- объем цилиндра, в котором находится заряд. В данном случаеVсовпадает с объемом гауссова цилиндра.

.

2) При x>d

.

Интегрирование в этом случае идет в пределах от до; в пределах отдозаряда нет, поэтому интеграл обращается в нуль.

Если непрерывно уменьшать толщину пластинки d, одновременно увеличивая плотность электричества₀, чтобы величинаоставалась постоянной, то в пределе получится бесконечная равномерно заряженная плоскость с поверхностной плотностью электричества, а напряженность поля будет определяться формулой, полученной в предыдущей задаче.

Пример 2.13.Какое поле создавали бы две безграничные плоскости, если бы одна была заряжена с поверхностной плотностью заряда, а другая -, и плоскости были перпендикулярны друг другу?

Решение.

Воспользуемся формулой напряженности равномерно заряженной плоскости, полученной в задаче 2.11:.

Тогда напряженности полей плоскостей равны:

.

Напряженность общего поля определим по теореме Пифагора (Рис. 2.10):

.

Это поле является однородным, и вектор напряженности составляет некоторый угол с плоскостью одной из пластин. Проведенные расчеты справедливы вдали от линии пересечения пластин.