§8. Переменный ток

I. Краткие теоретические сведения

Переменный ток представляет собой вынужденные электрические колебания. Переменный ток низкой частоты получают с помощью индукционного генератора, высокой частоты – с помощью генератора на транзисторе.

При расчете и анализе электрических цепей применяют несколько способов представления синусоидальных электрических величин.

Переменный ток представляет собой вынужденные электрические колебания. Переменный ток низкой частоты получают с помощью индукционного генератора, высокой частоты – с помощью генератора на транзисторе.

При расчете и анализе электрических цепей применяют несколько способов представления синусоидальных электрических величин.

1. Аналитический способ

Выражения для тока, напряжения и э. д. с. имеют вид

,

где I_m, U_m, E_m - амплитуды тока, напряжения и э. д. с., _I, _U, _ - начальная фаза тока, напряжения и э. д. с.

2. Временная диаграмма

Временная диаграмма представляет графическое изображение синусоидальной величины в заданном масштабе в зависимости от времени (рис. 8.1).

3. Графоаналитический способ

Графически синусоидальные величины изображаются в виде вращающегося вектора (рис. 8.2). Предполагается вращение против часовой стрелки с частотой вращения . Величина вектора в заданном масштабе представляет амплитудное значение. Проекция на вертикальную ось есть мгновенное значение величины. Совокупность векторов, изображающих синусоидальные величины (ток, напряжение, ЭДС) одной и той же частоты называют векторной диаграммой.

В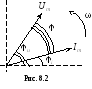основе графоаналитического способа анализа цепей переменного тока лежит построение векторных диаграмм. Для того, чтобы построить векторную диаграмму напряжений и токов при вынужденных колебаниях в электрической цепи, нужно знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для всех участков цепи.

Рассмотрим по отдельности случаи подключения внешнего источника переменного тока к резистору с сопротивлением , конденсатору емкостии катушки индуктивности. Во всех трех случаях напряжения на резисторе, конденсаторе и катушке равны напряжению источника переменного тока.

Резистор в цепи переменного тока

.

Фазовый сдвиг между током и напряжением на резисторе равен нулю. Связь между амплитудами тока и напряжения на резисторе выражается соотношением

.

Конденсатор в цепи переменного тока

Ток опережает по фазе напряжение на угол . Соотношение между амплитудами токаи напряжения

.

Катушка в цепи переменного тока

.

Ток отстает по фазе от напряжения на угол . Соотношение между амплитудами токаи напряжения.

.

Построим векторную диаграмму для последовательного -контура, в котором происходят вынужденные колебания на частоте. Поскольку ток, протекающий через последовательно соединенные участки цепи, один и тот же, векторную диаграмму удобно строить относительно вектора, изображающего колебания тока в цепи. Амплитуду тока обозначим через. Фазу тока примем равной нулю, что возможно, так как физический интерес представляют не абсолютные значения фаз, а относительные фазовые сдвиги. Векторная диаграмма для последовательного-контура изображена на рис. 8.3.

Векторная диаграмма на рис. 8.3 построена для случая, когда . В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол. Из рисунка видно, что

откуда следует

Для сравнения действий постоянного и переменного токов вводят понятие действующее значение переменного тока. Действующее значение переменного тока численно равно такому постоянному току, при котором за время равное одному периоду в проводнике с сопротивлением выделяется такое же количество тепловой энергии, как и при переменном токе. Действующие значения тока и напряжения определяются из выражения:

, ,

где - период изменения тока,- мгновенные значения тока и напряжения.

Действующие значения тока и напряжения для синусоидального тока соответственно равны:

.