§7. Колебательный контур

I. Краткие теоретические сведения

Колебательный контур– это электрическая цепь, содержащая катушку индуктивности и конденсатор, в которой могут возбуждаться электрические колебания. Свойства колебательного контура определяются его параметрами: индуктивностью, емкостью и сопротивлением.

Уравнение колебательного контура, содержащего последовательно соединенные конденсатор , катушку индуктивности, активное сопротивлениеи внешнюю переменную э. д. с.E. Тогда уравнение колебательного контура имеет вид

или

,

где -коэффициент затухания, – собственная частота.

Если E, то колебания называются свободными. Приони будут незатухающими, при- затухающими.

Уравнение свободных незатухающих колебанийпредставляет собой частный случай уравнения (7.1), когдаEи

,

его решение

,

где - амплитудное значение заряда на обкладке конденсатора,- начальная фаза, причем обе постоянные определяются начальными условиями. Колебания в таком контуре происходят с периодом (формула Томсона)

.

Уравнение свободных затухающих колебанийпредставляет собой частный случай уравнения (7.1) приE= 0

,

решение которого имеет вид

,

где

.

Зная , можно найти напряжение на конденсаторе и ток в контуре как

,

где – начальная амплитуда,

,

где уголопределяется из формул

.

При гармонических вынужденных колебаниях в контур включена внешняя переменная э. д. с. E зависящая от времени по гармоническому закону

.

Тогда уравнение колебательного контура (7.1)принимает вид

,

Сила тока в этом случае меняется по закону:

,

амплитудные значения силы тока и напряжения связаны законом Ома

,

, ,.

Здесь и– индуктивное и емкостное сопротивления. Напряжение и ток сдвинуты по фазе на угол.

II. Примеры решения задач

Пример 7.1.Ток в колебательном контуре зависит от времени как, гдемА,с^-1. Емкость конденсаторамкФ. Найти индуктивность контура и напряжение на конденсаторе в момент.

Решение.

По условию задачи ток изменяется по закону , т.е. в контуре (рис.6.1) происходят свободные незатухающие колебания, а уравнение колебательного контура имеет вид

,

где . Отсюда. Тогда

.

Для определения постоянной, используем начальным условиям: при ток. Так как

,

получим

, .

Откуда . Подстановкой, найдем

.

Пример 7.2.В контуре, состоящем из конденсатора емкостии катушки индуктивности, совершаются свободные незатухающие колебания, при которых амплитуда напряжения на конденсаторе равна. Найти связь между токомв контуре и напряжениемна конденсаторе.

Решение.

Уравнение колебательного контура в котором происходят свободные незатухающие колебания можно записать в виде

.

Умножим это уравнение на , получим

Подставляя ив последнее уравнение, имеем

.

Интегрируя последнее уравнение, окончательно получим

.

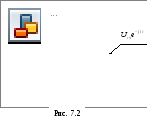
Пример 7.3.В контуре совершаются затухающие свободные колебания, при которых напряжение на конденсаторе меняется во времени по закону. Найти моменты времени, когда модуль напряжения на конденсаторе достигает:

а) амплитудных значений;

б) максимальных (экстремальных) значений.

Решение.

а). Из рис.7.2 видно, что модуль напряжения на конденсаторе достигает амплитудных значений при выполнении равенства , что возможно, если . Таким образом,

откуда

б). Для нахождения максимальных значений напряжения на конденсаторе следует приравнять нулю первую производную , т.о.

.

Отсюда получим, что , тогда , откуда

.

Пример 7.4. Найти коэффициент затухания и частоту свободных затухающих колебаний контура

(см. рис. 7.3).

Решение.

По второму закону Кирхгофа

.

Так как колебания свободные, то E = 0. Подставив значения напряжений, получим

,

или

О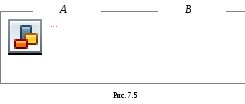ткуда

, .

П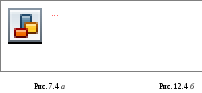ример 7.5.Некоторый колебательный контур содержит две последовательно соединенные катушки с активными сопротивлениями,и индуктивностями,, причем взаимная индуктивность пренебрежимо мала. Эти катушки нужно заменить одной так, чтобы частота и добротность не изменялась. Найтиитакой катушки.

Решение.

По условию задачи схему, изображенную на рис. 7.4 а, нужно заменить эквивалентной схемой, показанной на рис. 7.4б.

Запишем уравнение колебательного контура для первой схемы (рис. 7.4 а), полученное в предыдущем примере

,

тогда

, .

Собственная частота колебательного контура, изображенного на второй схеме, равна . Приравнивая частоты, найдем.

Приравняв добротности, получим

,

откуда

.

Пример 7.6. Имеются два колебательных контура (рис. 7.5). При каком соотношении между индуктивностями частоты свободных колебаний в контурах одинаковы?

Решение.

Запишем уравнения колебательного контура А, воспользовавшись первым законом Кирхгофа для замкнутых контуров и

откуда

,

тогда собственная частота равна

.

Уравнение колебательного контура В имеет вид

,

или

,

т.е. или собственная частота равна

.

По условию задачи частоты свободных колебаний в контурах одинаковы , тогда

.