§1. Напряженность электростатического поля. Потенциал.

I. Краткие теоретические сведения

Точечным зарядомназывается заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих электрический заряд.

Закон Кулона:Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними. Направление силы совпадает с соединяющей эти заряды прямой.

,

где k– коэффициент пропорциональности,q₁иq₂– величины взаимодействующих зарядов,r– расстояние между ними,e₁₂– единичный вектор направленный от заряда1к заряду2,F₁₂– сила, действующая на заряд2со стороны заряда1.

Коэффициент kопределяется следующим образом:

,

где ₀= 8,85 10^-12Ф/м – электрическая постоянная.

Напряженность поля, создаваемого точечным зарядомqпрямо пропорциональна заряду и обратно пропорциональна квадрату расстояния от заряда до данной точки поля:

,

вектор направлен вдоль прямой, проходящей через заряд и данную точку поля, от заряда, если он положителен, и к заряду, если он отрицателе.

Принцип суперпозиции: напряженность поля системы зарядов равна векторной сумме напряженностей полей, создаваемых каждым зарядом в отдельности:

.

Потенциал поля точечного заряда:

.

По принципу суперпозиции потенциал системы точечных зарядов равен:

.

II. Примеры решения задач

Пример 1.1.Тонкая проволока, представляющая по форме четверть кольца радиусаR, заряжена равномерно зарядомq. Найти напряженность поля в центре кривизны.

Решение.

Выбираем на кольце элементарный заряд , гдеиd- угол под которым из центра кривизны виден элементdl. Напряженность поля, создаваемого этим элементарным зарядом, равна:

Рис.1.1

.

Введем оси координат и находим проекции напряженности поля на выбранные оси:

.

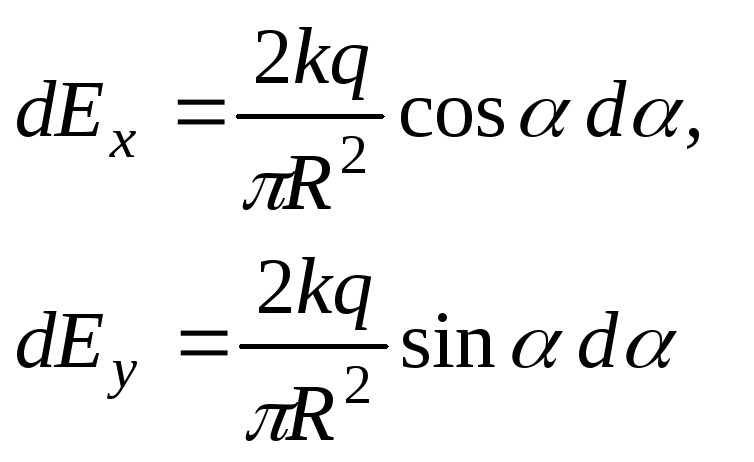Тогда:

.

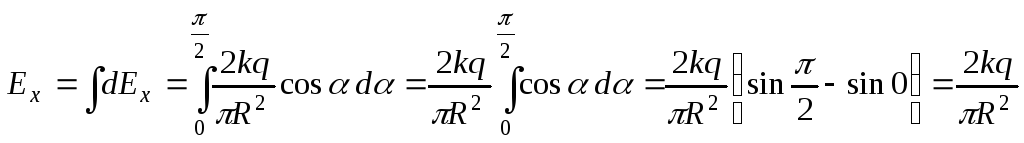
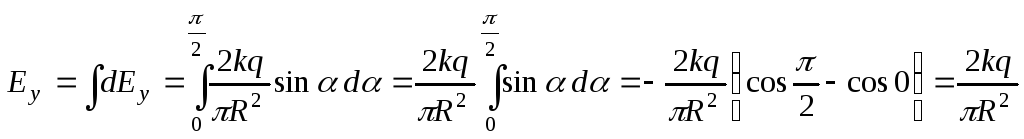Тогда суммарная напряженность будет равна:

.

Вектор напряженности направлен под углом 45к осих.

Пример 1.2Находящейся в вакууме тонкий прямой стержень длины 2азаряжен равномерно с зарядомq. Найти модуль напряженности электрического поля как функцию расстоянияrот центра стержня до точки прямой, совпадающей с осью стержняr >a.

Решение.

Вводим обозначения: . Выделим на стержне элементdl, заряд этого элемента равен:. Напряженность поля, создаваемого в точке наблюдения таким зарядом равна:

,

где l– расстояние от центра стержня до элементаdl. Поле, создаваемое всем стерж7нем будет равно:

Рис. 1.2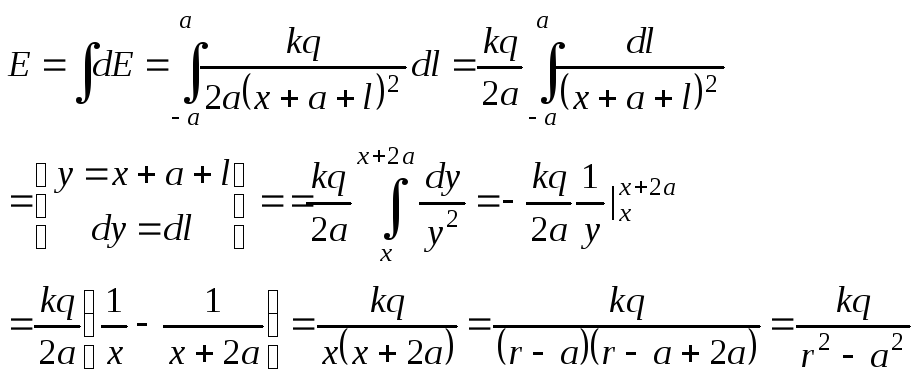

III. Задачи для самостоятельного решения

1.1.Кольцо радиусаRимеет зарядq. Найти модуль напряженности электрического поля на оси кольца как функцию расстоянияLдо его центра.

Ответ:.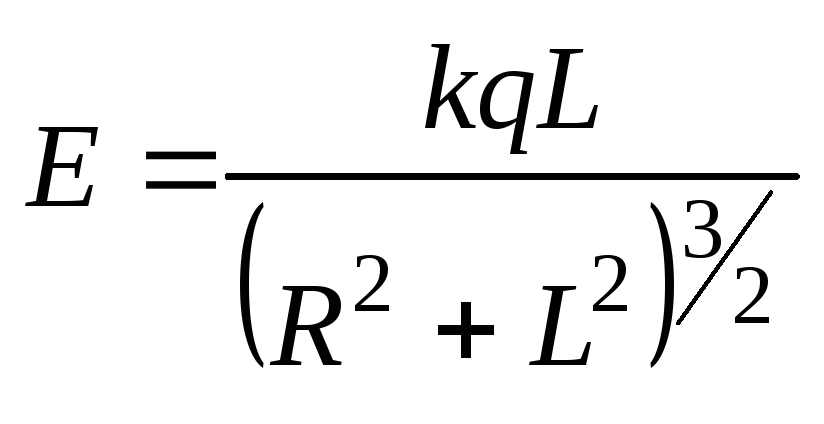

1.2.Тонкая проволока, представляющая по форме кольцо радиусаR, заряжена равномерно зарядомq. Найти напряженность поля в центре кольца.

Ответ:.

1.3.Тонкое полукольцо радиусаRимеет положительный зарядq. Найти напряженность в центре кривизны этого полукольца.

Ответ:.

1.4. Тонкая проволока, представляющая по форме три четверти кольца радиусаR, заряжена равномерно зарядомq. Найти напряженность поля в центре кривизны.

Ответ:.

1.5. Тонкое непроводящее кольцо радиусаRзаряжено с линейной плотностью, где- азимутальный угол. Найти напряженность: а) в центре кольца, б) на оси кольца в зависимости от расстоянияL.

Ответ:.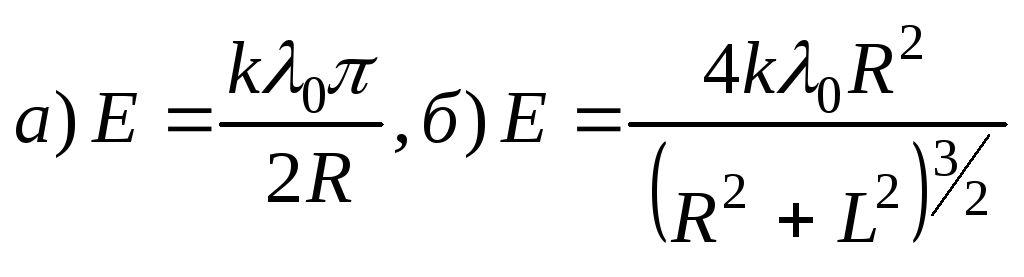

1.6. Тонкое непроводящее кольцо радиусаRзаряжено с линейной плотностью, где- азимутальный угол. Найти напряженность в центре кольца.

Ответ:.

1.7.Очень длинная прямая нить заряжена с линейной плотностью. Найти модуль и направление напряженности электрического поля в точке, которая отстоит от нити на расстояниеLи находится на перпендикуляре к нити.

Ответ:.

1.8. Очень длинная прямая нить заряжена с линейной плотностью. Найти модуль и направление напряженности электрического поля в точке, которая отстоит от нити на расстояниеLи находится на перпендикуляре к нити, проходящем через один из ее концов.

Ответ:.

1.9. Тонкий прямой стержень длины 2а равномерно заряжен с линейной плотностью. НайтиE(L), гдеL-расстояние от центра стержня до точки прямой, перпендикулярной стержню и проходящей через его центр.

Ответ:.

1.10.Тонкий прямой стержень длины 2а равномерно заряжен с линейной плотностью. НайтиE(L), гдеL-расстояние от центра стержня до точки прямой совпадающей с осью стержня, если.

Ответ:.

1.11.Равномерно заряженная нить, на единицу длины которой приходится заряд, имеет конфигурацию, показанную на рис.1.3. Радиус закругленияRгораздо меньше длинны нити. Найти модуль напряженности электрического поля в точке О.

Ответ:.

1.12.Находящаяся в вакууме тонкая пластинка радиусаRравномерно заряжена с поверхностной плотностью. Найти модуль напряженности электрического поля на оси пластинки как функцию расстоянияLот ее центра.

Ответ:.

1.13. Плоское кольцо, внутренний радиус которого а, внешний в, заряжено с поверхностной плотностью. Найти модуль напряженности электрического поля на оси кольца как функцию расстоянияLот его центра.

О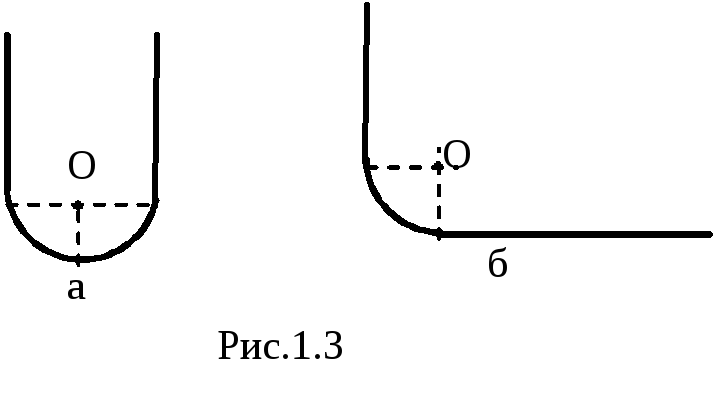твет:.

1.14.Зарядqраспределен равномерно по объему шара радиусаR. Найти потенциал:

а) в центре шара ₀, б) внутри шара(r), в) вне шара(r), гдеr- расстояние от центра шара.

Ответ:.

1.15. Потенциал поля внутри заряженного шара, гдеаиb– постоянные. Найти зависимость объемной плотности заряда(r) от расстояния от центра шара.

Ответ:.

1.16.По сфере радиусаRравномерно распределены заряды с поверхностной плотностьюНайти потенциал в зависимости от расстояния до центра сферы.

Ответ:.

1.17. Плоское кольцо, внутренний радиус которогоа, внешнийb, заряжено с поверхностной плотностью. Найти потенциал в центре кольца.

Ответ:.

1.18.Находящаяся в вакууме тонкая пластинка радиусаRравномерно заряжена с поверхностной плотностью. Найти потенциал электрического поля на оси пластинки как функцию расстоянияLот ее центра.

Ответ:.

1.19. Две длинные одноименно заряженные нити расположены на расстояниидруг от друга. Линейная плотность заряда на нитях. Найти величину и направление напряженности результирующего электрического поля в точке, находящейся на расстоянииот каждой нити.

Ответ:.