Решение типовых примеров

Пример 1. Решить уравнение

Решение:Перепишем исходное уравнение в виде

Разделив обе части последнего уравнения на , получим:

или .

Случаю отвечают два дополнительных решения. Отметим, что уравнение можно упростить, взяв синус от обеих его частей:

Ответ:,.

Пример 2.

Решение: (Разделили данное уравнение на). Тогда

.

Дополнительные решения , определяемые из условия, получаются из общего интеграла при.

Ответ: .

Пример 3. Найти решение уравнения , удовлетворяющее начальному условию.

Решение:

(подставили в общий интеграл начальные условия ), .

Ответ:.

Пример 4. Решить уравнение .

Решение:(tgx tgy 0),

, .

Ответ:

Пример 5. Решить уравнение .

Решение:

, .

Так как ‑ решения, то.

Ответ: .

Пример 6. Решить уравнение

Решение:где;

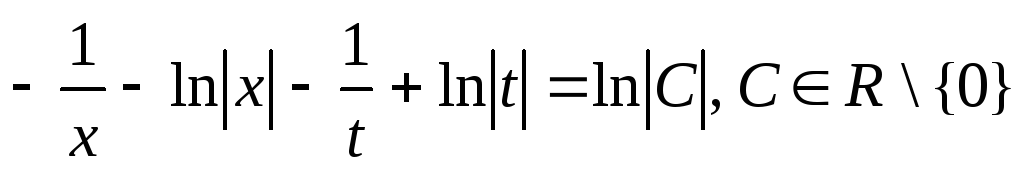или

а так как ‑ решение, то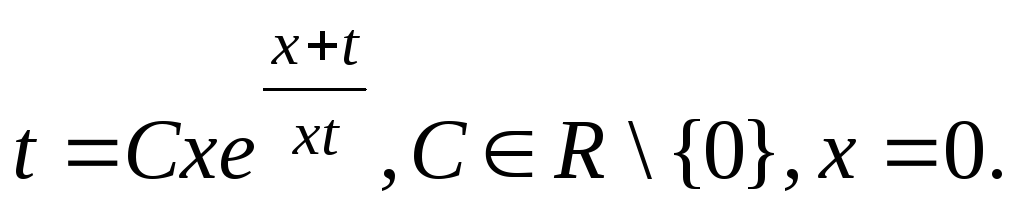

Ответ:.

Пример 7. Решить уравнение.

Решение:

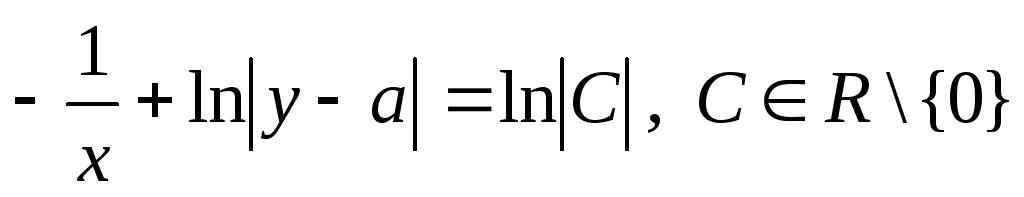. Но – решение, поэтому

Ответ:.

Пример 8. Решить уравнение

Решение:

Ответ:

Пример 9. Решить уравнение

Решение:

Ответ:

Пример 10. Решить уравнение

Решение:

Ответ:

Пример 11. 213.

Решение:

Ответ:

Задачи для самостоятельного решения

Решить уравнения:

1. ,прих=0Ответ:.

2. Ответ:

3. (1+ х²)dy+ydx= 0, y=1, при х=1. Ответ:

4. Ответ: (kZ), х=0

5. у=0 при х=1. Ответ:2е^-у(у+1)=х²+1.

6. при х=1. Ответ:

7. . Ответ:

8. у+cos(x+2y)=cos(x-2y), y= при х=0.Ответ:

9. Ответ:.

10. при . Ответ:.

11. при. Ответ:

12. Ответ:.

13. Ответ:

14. Ответ: x

15. Ответ:

16. Ответ:

17. Ответ:y = a.

18. Ответ:

19.

Ответ:

20.

Ответ: .

21. Ответ:

22.

Ответ:

23.

Ответ:

24. 5e^x tgydx+(1-e^x)sec²ydy=0 Ответ: y=

25. Ответ:

§2. Однородные уравнения

К уравнениям с разделяющимися переменными после надлежащей подстановки приводятся однородные уравнения. Под однородным дифференциальным уравнением 1-го порядка мы понимаем уравнение , когда в нем функцияпредставляет собой однородную функцию переменных и нулевой степени однородности и, следовательно, зависит от их отношения.

Функция называетсяоднородной степени k,если удовлетворяет тождеству

при любом .

Полагая , получаем: или . Оба переменных равноправны; поэтому также.

Таким образом, рассматриваемые уравнения будут вида:

. (1)

Подстановкой мы добиваемся разделения переменных. Так как, то; подставляя в уравнение (1), получаем:

,

или

(1.1)

предполагая, что и , разделяем переменные и интегрируем:

,

Обозначая через, получаем общий интеграл уравнения (1) в виде:

. (1.2)

Так как подстановка привела нас к уравнению с разделяющимися переменными, то, опираясь на теорему об этих уравнениях, можем утверждать, что если в некотором интервале ‑ непрерывна [а для этого достаточно непрерывности] и не обращается в нуль, то в области, такой, чтоа<и<b, , уравнение (1.1) имеет общий интеграл, выражаемый в квадратурах, и через каждую точку области Gпроходит единственная интегральная кривая. Это же справедливо и для данного уравнения (10), из которого уравнение (1.1) получено подстановкой!. При этом область(, илиах<у<bх, ), представляет внутреннюю часть двух вертикальных углов, ограниченных прямымиу=ах иу=bх,причем берутся те два угла, которые не содержат оси Oy,ибо.

Таким образом, является справедливой следующая теорема.

Теорема.Однородное дифференциальное уравнение при условии, чтонепрерывна ив интервале, имеет общий интеграл, выражаемый в квадратурах. При этом через каждую точку области , лежащей внутри вертикальных углов, ограниченных прямыми у=ах и у=bх и. не содержащей прямой , проходит единственная интегральная кривая.

В случае же, если найдутся такие значения и,при которых,каждому такому,будет отвечать решение, или,не вытекающее из общего интеграла.

Следует отметить, что в том случае, когда , дифференциальное уравнение является уравнением с разделяющимися переменными; для этого уравнения; как и вообще для уравнения (1) начало координатявляется особой точкой.

Уравнение в симметрическом виде

(2)

является однородным, когда ‑ однородные функции одной и той же степени однородности:

, .

В этом случае подстановка ,приводит к разделению переменных.

Интегрируемыми в квадратурах будут приводящиеся к однородным (или непосредственно к уравнениям с разделяющимися переменными) уравнения вида:

. (12)

Действительно, если определитель , то мы сумеем найти такиеи, что подстановкаипревратит это уравнение в однородное. Для этого нужно выбратьитак, чтобы

а это возможно, если . Выполняя подстановку, получим:

.

Это уравнение однородно, ибо .

В случае, если определитель ,элементы его строк пропорциональны:.Тогда, применяя подстановку , получаем: .Таким образом, приходим к уравнению с разделяющимися переменными;

.