
Диф.уры Прокофьев / DIFFER5
.DOC
Глава 5. УСТОЙЧИВОСТЬ
Дифференциальное уравнение или система, описывающие какой-либо физический процесс, обычно таковы, что участвующие в них функции, а также числовые коэффициенты и начальные условия задаются приближённо, с какой-либо степенью точности. Если решение уравнения меняется сильно при незначительном изменении этих данных, то такое решение неустойчиво, и появляются серьёзные сомнения в том, что эти функции действительно описывают данный процесс. Естественным требованием поэтому является устойчивость решений. Из различных понятий устойчивости мы выберем наиболее употребительное – устойчивость по Ляпунову.
Пусть
![]() (1)
система
дифференциальных уравнений, записанная
в векторной форме (здесь
(1)
система
дифференциальных уравнений, записанная
в векторной форме (здесь
![]() неизвестная вектор-функция), и
рассматриваются решения этой системы,
удовлетворяющие начальному условию
неизвестная вектор-функция), и
рассматриваются решения этой системы,
удовлетворяющие начальному условию
![]() и определённые на полуоси
и определённые на полуоси
![]() Решение
Решение
![]() называется устойчивым
по Ляпунову,
если для любого
называется устойчивым
по Ляпунову,
если для любого
![]() найдётся такое
найдётся такое
![]() что для всех
что для всех
![]() удовлетворяющих неравенству
удовлетворяющих неравенству
![]() решение
решение
![]() системы (1) с начальным условием
системы (1) с начальным условием
![]() продолжается на всю полуось
продолжается на всю полуось
![]() и для всех
и для всех
![]() имеет место неравенство
имеет место неравенство
![]() В противном случае решение
В противном случае решение
![]() называется неустойчивым.
называется неустойчивым.
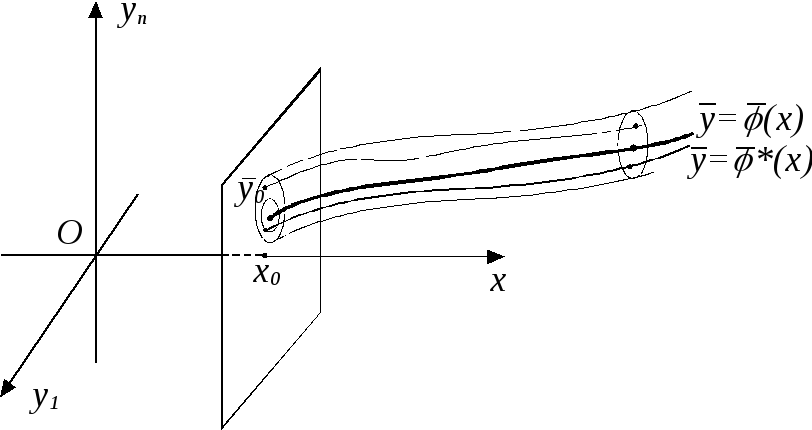
Дадим геометрическую
интерпретацию этому определению. Окружим
график функции
![]() “трубочкой”
(криволинейным
цилиндром) радиуса
“трубочкой”
(криволинейным
цилиндром) радиуса
![]() Устойчивость решения
Устойчивость решения
![]() означает, что для любого
означает, что для любого
![]() (т.е. любой “трубочки”)
найдётся такой “диск”
(т.е. любой “трубочки”)
найдётся такой “диск”
![]() что все решения, “выпущенные”
из “диска”,
будут
лежать внутри “трубочки”.
что все решения, “выпущенные”
из “диска”,
будут
лежать внутри “трубочки”.
Отметим теперь,
что вопрос об устойчивости решения
системы
![]() можно свести к вопросу об устойчивости
нулевого
решения
(т.е. функции, тождественно равной нулю)
некоторой другой системы. А именно,
положим
можно свести к вопросу об устойчивости
нулевого
решения
(т.е. функции, тождественно равной нулю)
некоторой другой системы. А именно,
положим
![]() Тогда
Тогда
![]() Таким образом, система (1) с неизвестной
функцией
Таким образом, система (1) с неизвестной
функцией
![]() равносильна системе
равносильна системе
![]() (2)
(2)
в которой неизвестной
функцией является
![]() При этом решению
При этом решению
![]() системы (1) соответствует нулевое решение
системы (2). Решение
системы (1) соответствует нулевое решение
системы (2). Решение
![]() системы (1) устойчиво в том и только том
случае, если устойчиво нулевое решение
системы (2). В дальнейшем мы будем
предполагать, что на
устойчивость исследуется нулевое
решение системы.
системы (1) устойчиво в том и только том
случае, если устойчиво нулевое решение
системы (2). В дальнейшем мы будем
предполагать, что на
устойчивость исследуется нулевое
решение системы.
Достаточное условие устойчивости даёт теорема Ляпунова, к изложению которой мы сейчас перейдём. Но перед этим определим функцию Ляпунова, участвующую в формулировке теоремы.
Функцией
Ляпунова
![]() называется дифференцируемая функция
называется дифференцируемая функция
![]() которая является положительно
определённой
в том смысле, что
которая является положительно
определённой
в том смысле, что
![]() при всех
при всех
![]() и
и
![]()
Примерами функций
Ляпунова могут служить
![]()
![]() (при
(при
![]()
![]() и т.д.
и т.д.
Теорема Ляпунова. Если для системы дифференциальных уравнений

существует функция
Ляпунова
![]() такая, что
такая, что
![]() для всех
для всех
![]() то нулевое решение системы устойчиво.
то нулевое решение системы устойчиво.
Доказательство теоремы разобьём на несколько пунктов.
-
Заметим, что если
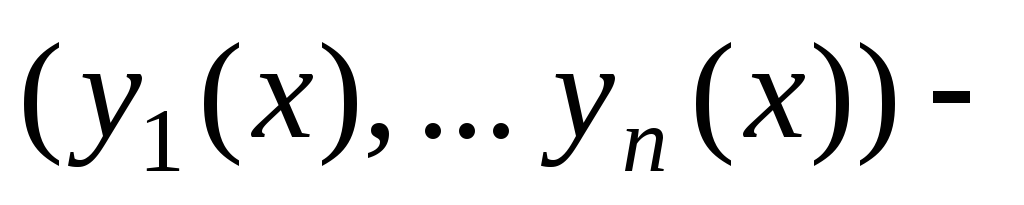 решение
системы, то, подставив
решение
системы, то, подставив
 в функцию Ляпунова, мы получим функцию
одного переменного
в функцию Ляпунова, мы получим функцию
одного переменного
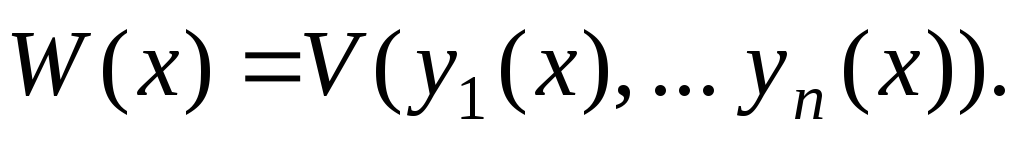 Эта функция убывающая (в нестрогом
смысле), так как
Эта функция убывающая (в нестрогом
смысле), так как

-
Рассмотрим сферу радиуса
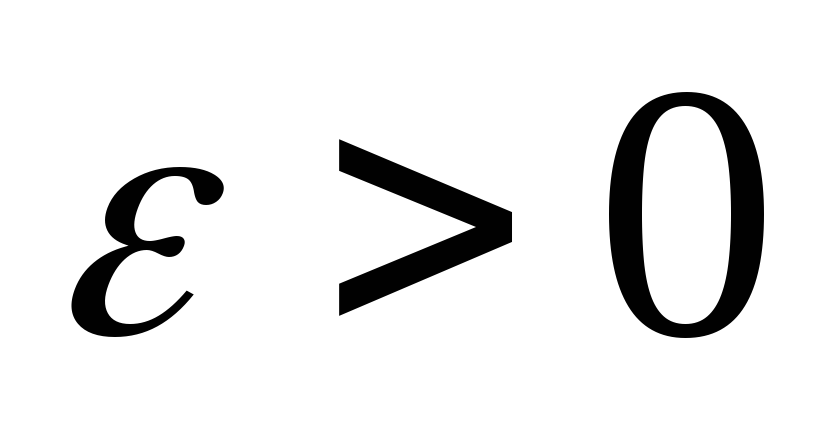 в пространстве
в пространстве
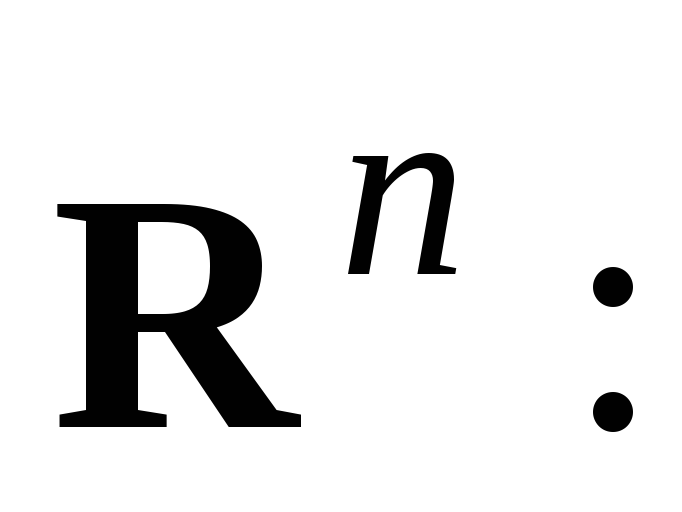
 Эта сфера является ограниченным
замкнутым подмножеством пространства
Эта сфера является ограниченным
замкнутым подмножеством пространства
 (компактом), поэтому существует
(компактом), поэтому существует
 Так как
Так как
 положительно определена, то
положительно определена, то
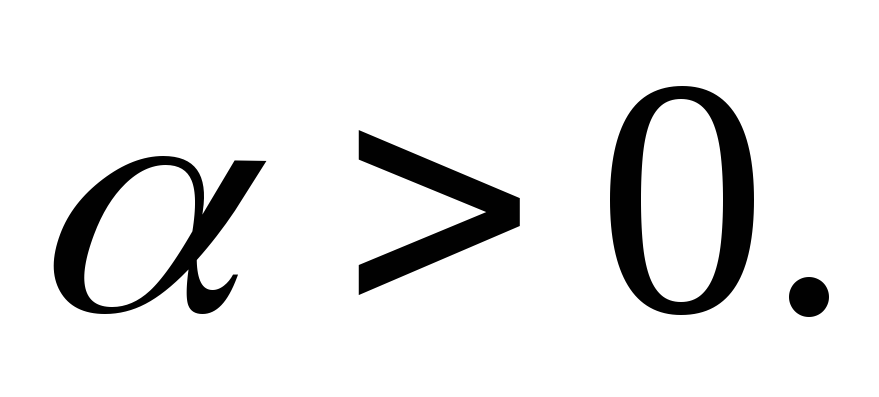
-
Ввиду непрерывности функции
 существует такое
существует такое
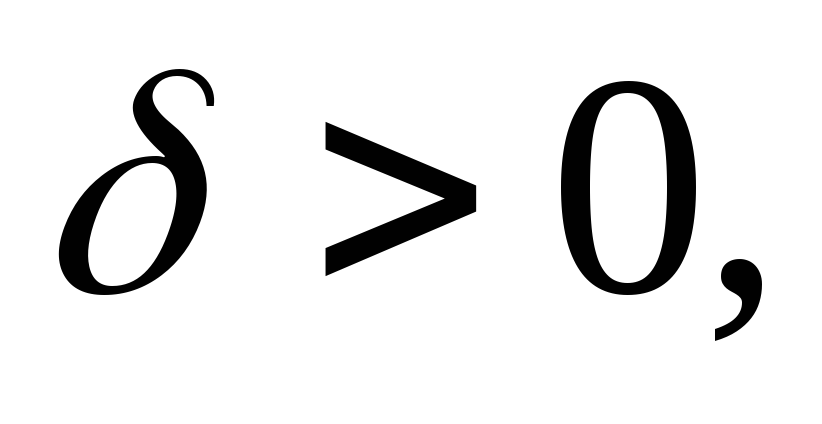 то
то
 при всех
при всех

-
Осталось проверить выполнение определения устойчивости. Пусть
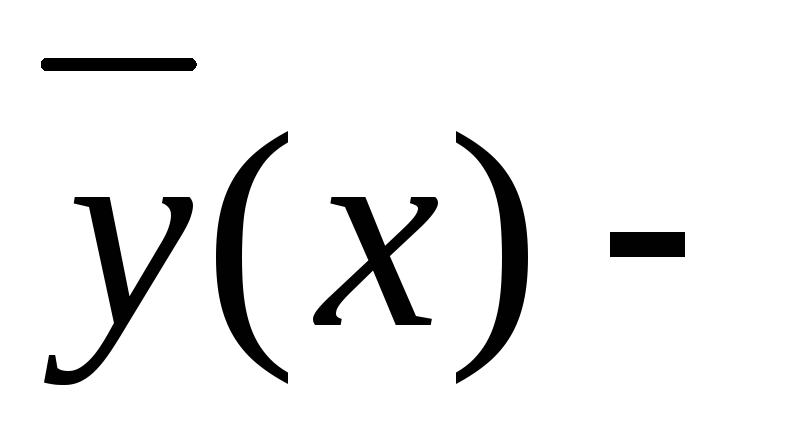 решение системы с начальным условием
решение системы с начальным условием
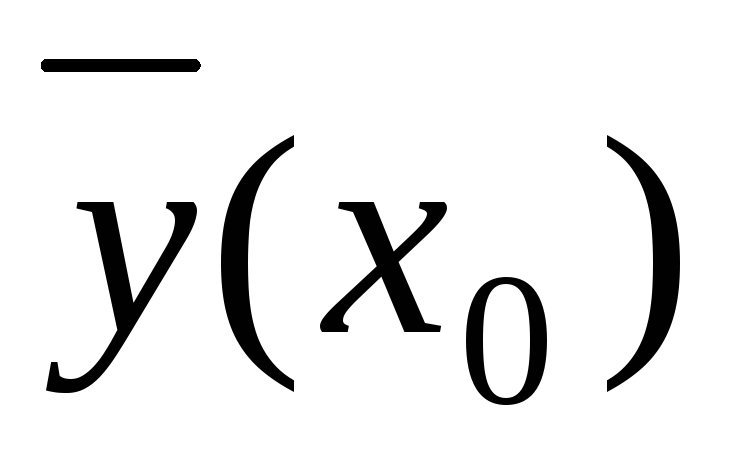 таким, что
таким, что
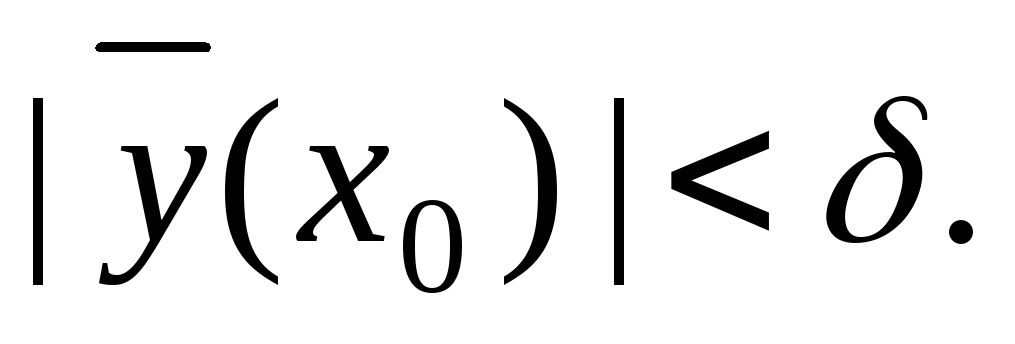 Для доказательства теоремы теперь
достаточно показать, что график функции
Для доказательства теоремы теперь
достаточно показать, что график функции
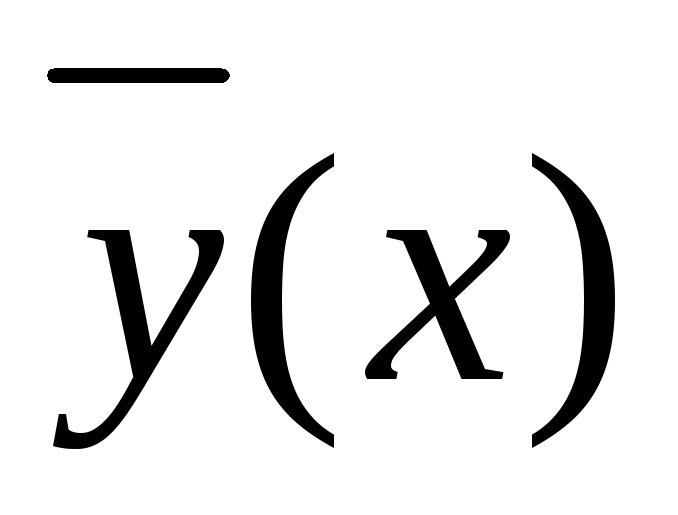 не выходит за пределы цилиндра радиуса
не выходит за пределы цилиндра радиуса
 т.е. что
т.е. что
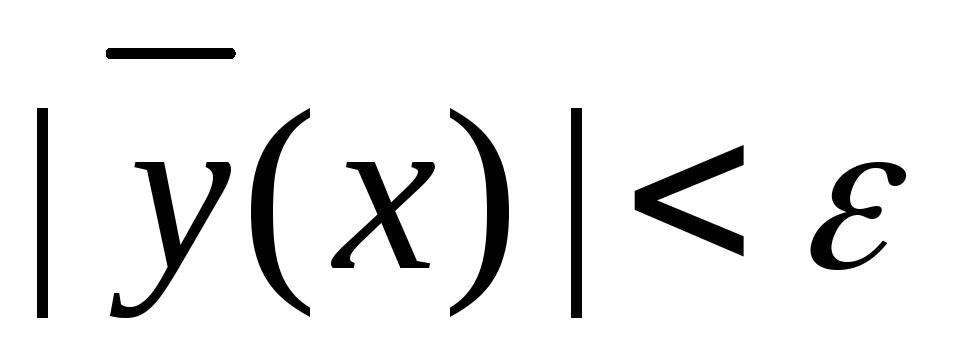 при всех
при всех
 Действительно, если
Действительно, если
 не для всех
не для всех
 и
и
 наименьшее значение, для которого
наименьшее значение, для которого
 то точка
то точка
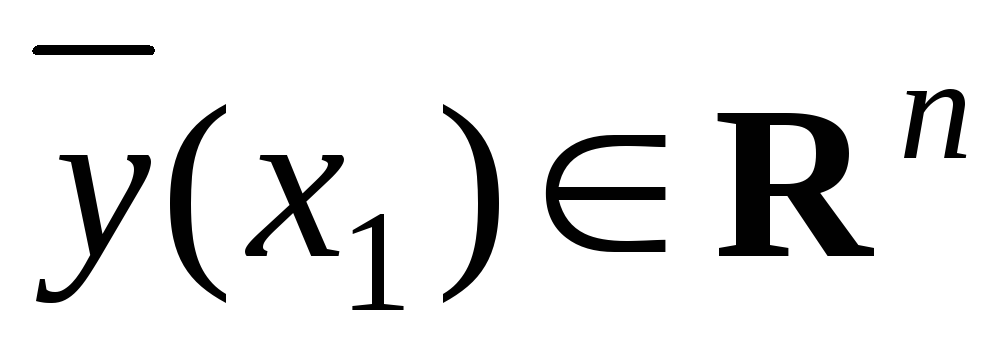 лежит на сфере
лежит на сфере
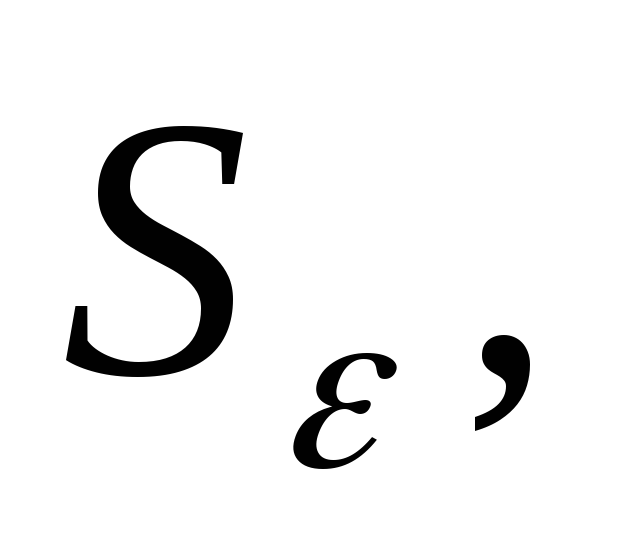 поэтому
поэтому
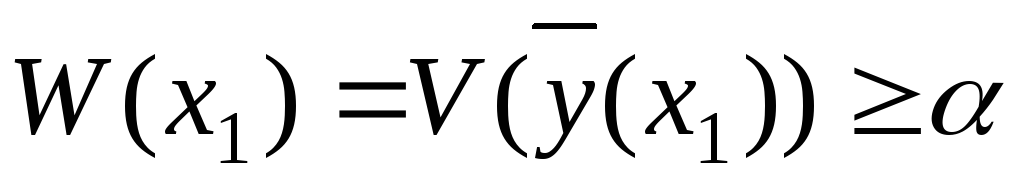 (см. пункт 2), а
(см. пункт 2), а
 (см. пункт 3). Итак, мы имеем:
(см. пункт 3). Итак, мы имеем:
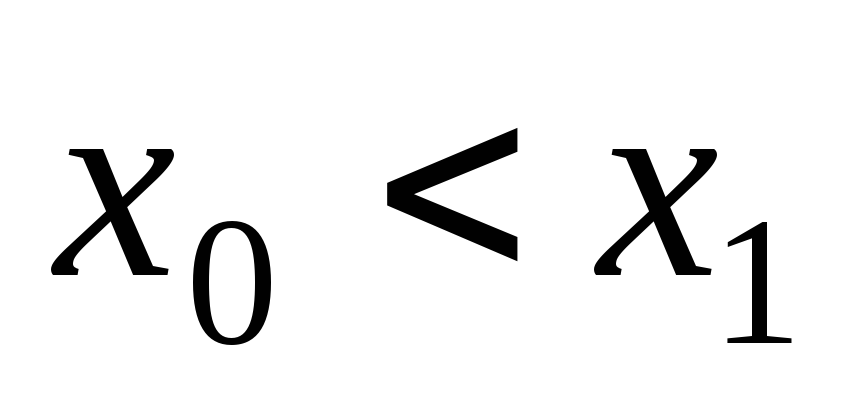 и
и
 а это противоречит доказанному в пункте
1 убыванию функции
а это противоречит доказанному в пункте
1 убыванию функции
 Теорема доказана.
Теорема доказана.
Устойчивость решений системы с постоянными коэффициентами оказывается тесно связанной с собственными значениями матрицы системы и в большинстве случаев полностью определяется ими, как показывает следующая теорема. Доказательство теоремы мы опустим, отсылая читателя к учебникам по дифференциальным уравнениям с более подробным изложением. Отметим лишь, что она может быть доказана с использованием теоремы Ляпунова и приведения матрицы системы к жордановой нормальной форме.
Теорема. Пусть дана система дифференциальных уравнений
![]()
где
![]()
![]() матрица размера
матрица размера
![]() с элементами
с элементами
![]()
![]() непрерывная вектор-функция, определённая
для
непрерывная вектор-функция, определённая
для
![]() Пусть
Пусть
![]() С
– собственные значения матрицы А.
Тогда:
С
– собственные значения матрицы А.
Тогда:
-
если
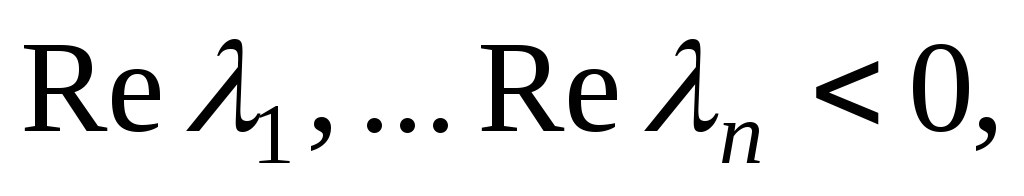 то всякое решение системы устойчиво;
то всякое решение системы устойчиво; -
если
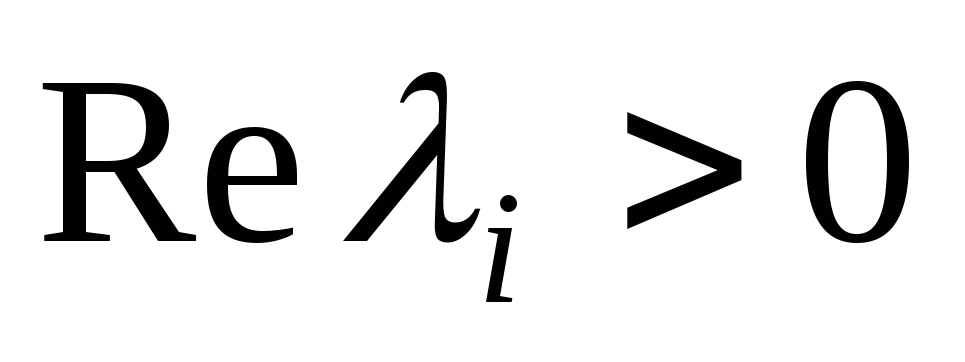 для какого-либо
для какого-либо
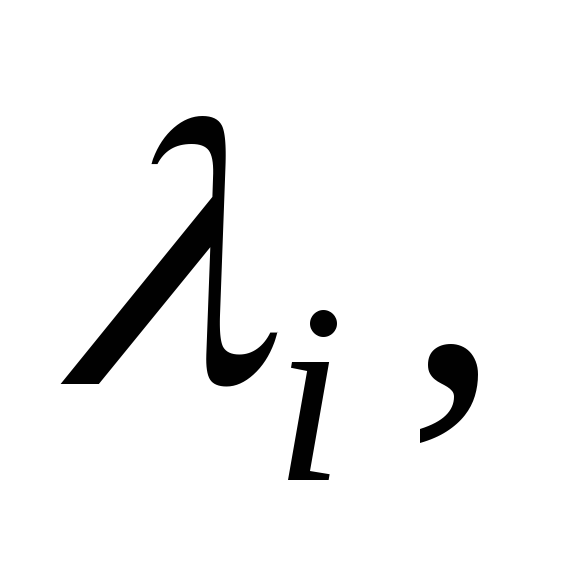 то всякое решение системы неустойчиво.
то всякое решение системы неустойчиво.
Теорема не даёт
ответа на вопрос об устойчивости решений
в случае, когда
![]() при всех
при всех
![]() и
и
![]() для какого-либо
для какого-либо
![]()
Нелинейные системы часто удаётся исследовать на устойчивость, осуществив линеаризацию системы, т.е. замену нелинейной на близкую к ней ( в определённом смысле) линейную систему. А именно, пусть система имеет вид
![]() (
(![]()
Выделим каким-либо
способом у функций
![]() главную линейную часть (т.е. разложим
функции
главную линейную часть (т.е. разложим
функции
![]() по формуле
Тэйлора до членов первого порядка):
по формуле
Тэйлора до членов первого порядка):
![]()
где
![]() а
а
![]() достаточно мала. Тогда вопрос об
устойчивости нелинейной системы сведётся
к аналогичному вопросу для линейной
системы с постоянными коэффициентами,
а он рассматривался в предыдущей
теореме. Точный математический смысл
высказанного утверждения даётся
следующей теоремой,
достаточно мала. Тогда вопрос об
устойчивости нелинейной системы сведётся
к аналогичному вопросу для линейной
системы с постоянными коэффициентами,
а он рассматривался в предыдущей
теореме. Точный математический смысл
высказанного утверждения даётся
следующей теоремой,
доказательство которой здесь не приводится и может быть найдено в учебниках по дифференциальным уравнениям с более подробным изложением.
Теорема об
устойчивости по первому приближению.
Пусть дана система дифференциальных
уравнений
![]() где
где
![]() постоянная
постоянная
![]() -матрица,
а вектор-функция
-матрица,
а вектор-функция
![]() удовлетворяет условию
удовлетворяет условию
![]() при
при
![]() для некоторой константы
для некоторой константы
![]() Пусть
Пусть
![]() собственные значения матрицы А.
Тогда:
собственные значения матрицы А.
Тогда:
-
если
 то нулевое решение системы устойчиво;
то нулевое решение системы устойчиво; -
если
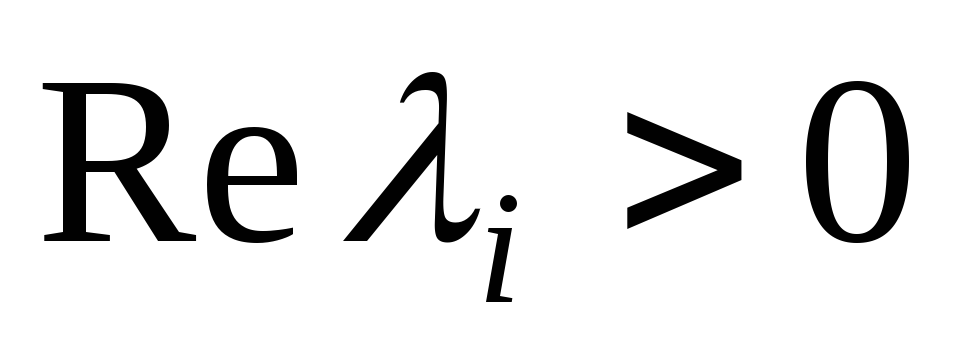 при некотором
при некотором
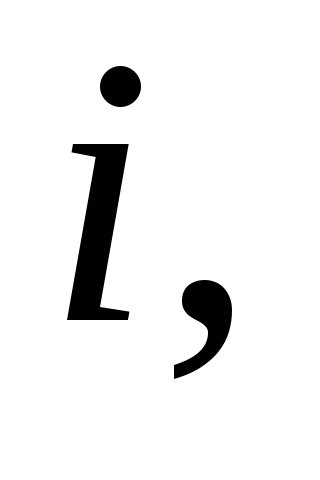 то нулевое решение системы неустойчиво.
то нулевое решение системы неустойчиво.
Примеры решения задач
-
Определить устойчивость решения уравнения п-го порядка
![]()
с начальным условием
![]()
![]()
Решение.
Устойчивость означает, что небольшое
изменение начальных условий не вызывает
значительного изменения решения. Поэтому
решение
![]() естественно назвать устойчивым, если
для любого
естественно назвать устойчивым, если
для любого
![]() существует такое
существует такое
![]() что для любого набора чисел
что для любого набора чисел
![]() таких, что
таких, что
![]() решение с начальным условием
решение с начальным условием
![]() существует на всей полуоси
существует на всей полуоси
![]() м для всех
м для всех
![]() удовлетворяет неравенству
удовлетворяет неравенству
![]()
-
Пользуясь лишь определением устойчивости, выяснить, устойчивы ли решения данных уравнений с заданными начальными условиями:
а)
![]() б)
б)
![]()
Решение.
а) Данное уравнение является уравнением
с разделяющимися переменными. Имеем:
![]() откуда
откуда
![]() Это общее решение данного уравнения.
Чтобы найти решение, удовлетворяющее
данному начальному условию, надо
подставить в эту формулу
Это общее решение данного уравнения.
Чтобы найти решение, удовлетворяющее
данному начальному условию, надо
подставить в эту формулу
![]() Получим
Получим
![]() а значит,
а значит,
![]() Пусть
Пусть
![]() решение уравнения с другим начальным
условием. Для устойчивости необходимо,
чтобы
решение уравнения с другим начальным
условием. Для устойчивости необходимо,
чтобы
![]() т.е.
т.е.
![]() Но каково бы ни было число С,
отличное от нуля, всегда можно найти
достаточно большое
Но каково бы ни было число С,
отличное от нуля, всегда можно найти
достаточно большое
![]() для которого
для которого
![]() Следовательно, решение уравнения
неустойчиво.
Следовательно, решение уравнения
неустойчиво.
б) Решения этого
уравнения имеют вид
![]() Эти функции определены на всей
действительной оси. Кроме того,
Эти функции определены на всей
действительной оси. Кроме того,
![]() Значит, решение, проверяемое на
устойчивость, – это
Значит, решение, проверяемое на
устойчивость, – это
![]() Функция
Функция
![]() имеет на промежутке
имеет на промежутке
![]() максимум
максимум
![]() Поэтому
Поэтому
![]() Это доказывает устойчивость. Здесь
Это доказывает устойчивость. Здесь
![]()
-
Какие из следующих функций являются функциями Ляпунова:
а)
![]() б)
б)
![]() в)
в)![]()
Решение.
а) Функция
![]() дифференцируема и положительно
определена, поэтому является функцией
Ляпунова.
дифференцируема и положительно
определена, поэтому является функцией
Ляпунова.
б) Эта функция не
является положительно определённой,
так как
![]() Следовательно, эта функция не является
функцией Ляпунова.
Следовательно, эта функция не является
функцией Ляпунова.
в) Функция
![]() недифференцируема в точке
недифференцируема в точке
![]() поэтому не является функцией Ляпунова.
поэтому не является функцией Ляпунова.
-
Доказать устойчивость нулевого решения системы, используя функцию Ляпунова: а)
 б)
б)
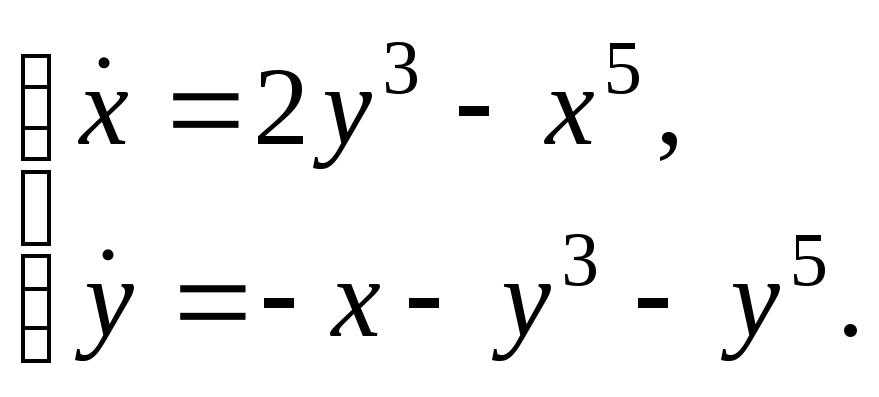
Решение.
а) Возьмём в качестве функции Ляпунова
функцию
![]() Имеем:
Имеем:
![]() при всех
при всех
![]() Следовательно, нулевое решение системы
устойчиво.
Следовательно, нулевое решение системы
устойчиво.
б) Положим
![]() Тогда
Тогда
![]() Следовательно, по
теореме Ляпунова нулевое решение системы
устойчиво.
Следовательно, по
теореме Ляпунова нулевое решение системы
устойчиво.
-
Выяснить, устойчивы ли решения системы:
а)
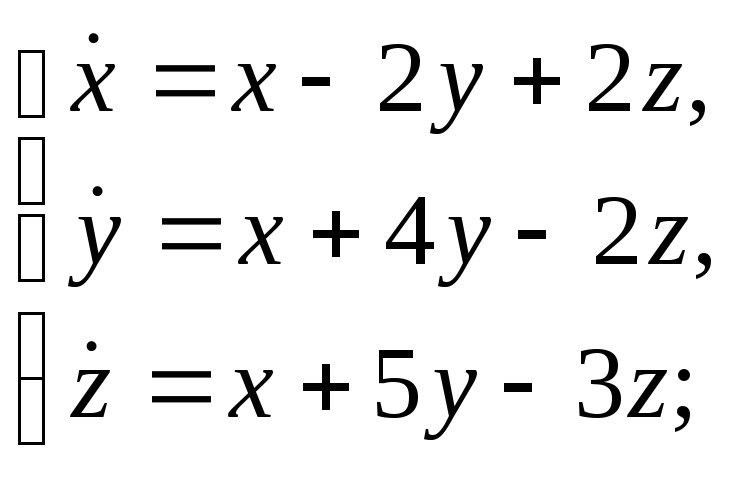 б)
б)
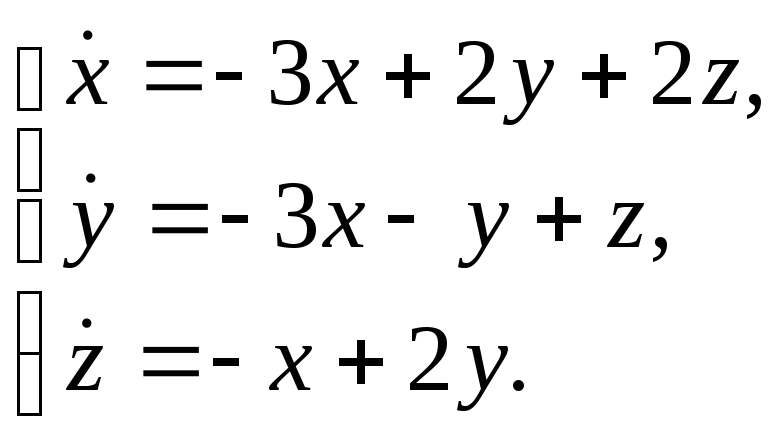
Решение.
а) Найдём собственные значения матрицы
системы
 Для этого решим характеристическое
уравнение
Для этого решим характеристическое
уравнение
![]() Имеем:
Имеем:
 Корни этого
кубического уравнения следующие:
Корни этого
кубического уравнения следующие:
![]()
![]()
![]() Так как существует
Так как существует
![]() то решения системы неустойчивы.
то решения системы неустойчивы.
б) Решая
характеристическое уравнение
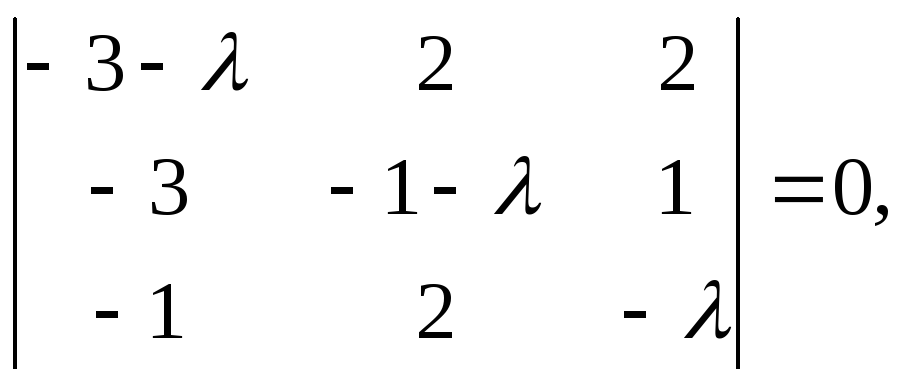 получаем:
получаем:
![]()
![]() Так как
Так как
![]() и
и
![]() то решения системы устойчивы.
то решения системы устойчивы.
-
Найти интервал изменения параметра
 на котором нулевое решение системы
на котором нулевое решение системы
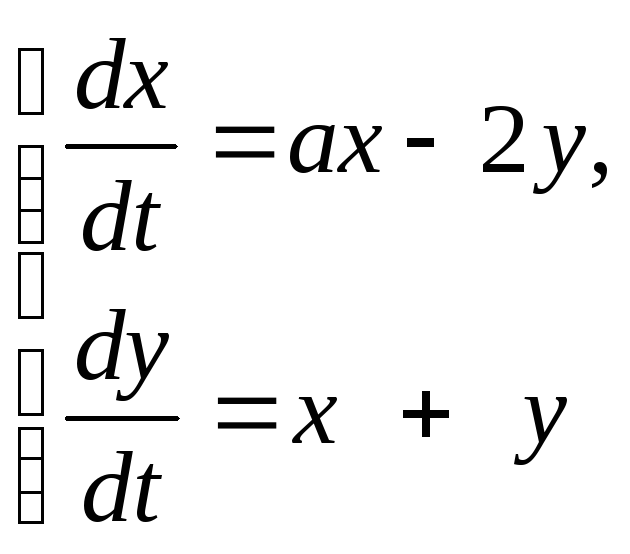 является устойчивым.
является устойчивым.
Решение.
Найдём собственные значения матрицы
системы
![]() Имеем:
Имеем:
 Отсюда
Отсюда
![]() Возможны два случая:
Возможны два случая:
![]() и
и
![]() В первом случае
В первом случае
![]() или
или
![]() а оба корня
а оба корня
![]() действительные числа. Для устойчивости
нужно, чтобы оба корня были меньше нуля,
что равносильно выполнению неравенства
действительные числа. Для устойчивости
нужно, чтобы оба корня были меньше нуля,
что равносильно выполнению неравенства
![]() Решив это неравенство, получим:
Решив это неравенство, получим:
![]() Во втором случае
Во втором случае
![]() и оба корня комплексные. Имеем:
и оба корня комплексные. Имеем:
![]() Для устойчивости нужно, чтобы
Для устойчивости нужно, чтобы
![]() Следовательно,
Следовательно,
![]() Объединив оба случая, получим:
Объединив оба случая, получим:
![]() Это наибольший интервал устойчивости.
Это наибольший интервал устойчивости.
-
Исследовать на устойчивость нулевое решение системы, используя теорему об устойчивости по первому приближению:
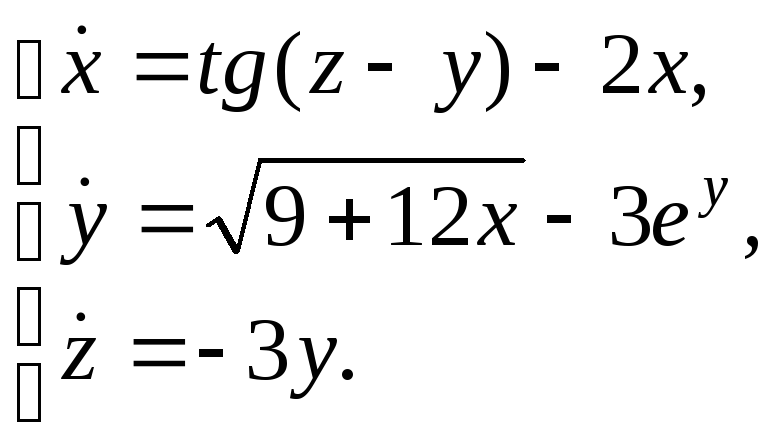
Решение.
При малых
![]() мы имеем:
мы имеем:
![]() где
где
![]()
![]()
![]() Таким образом,
система имеет вид
Таким образом,
система имеет вид
 где
где
![]() Исследуем теперь на устойчивость
линеаризованную систему, т.е. линейную
систему, полученную отбрасыванием
слагаемых
Исследуем теперь на устойчивость
линеаризованную систему, т.е. линейную
систему, полученную отбрасыванием
слагаемых
![]() Найдём собственные значения:
Найдём собственные значения:
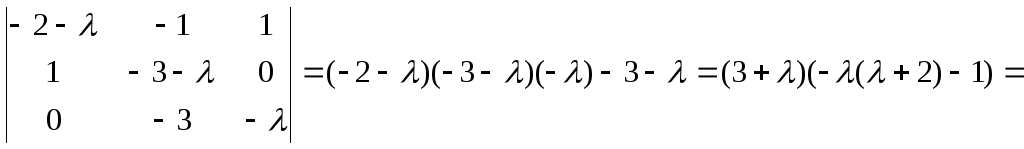
![]() откуда
откуда
![]()
![]() Так как
Так как
![]()
![]()
![]() то по теореме об устойчивости по первому
приближению мы получаем, что нулевое
решение исходной системы (нелинейной)
устойчиво.
то по теореме об устойчивости по первому
приближению мы получаем, что нулевое
решение исходной системы (нелинейной)
устойчиво.
-
Исследовать на устойчивость нулевое решение уравнения
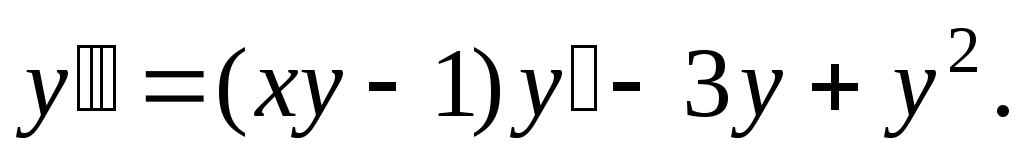
Решение.
Полагая
![]() сведём уравнение к системе, получим:
сведём уравнение к системе, получим:
 Линеаризованная система имеет вид
Линеаризованная система имеет вид
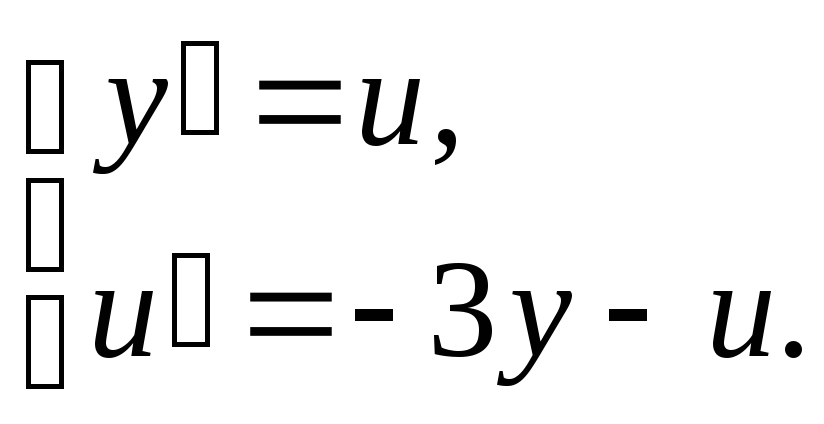 Найдём собственные значения её матрицы:
Найдём собственные значения её матрицы:
![]()
![]() Так как
Так как
![]() то нулевое решение системы устойчиво.
то нулевое решение системы устойчиво.
Задачи для самостоятельного решения
-
Используя лишь определение устойчивости, выяснить, устойчивы ли решения данных уравнений с заданными начальными условиями:
а)
![]()
![]() б)
б)
![]()
![]()
-
Доказать устойчивость нулевого решения системы, используя функцию Ляпунова:
а)
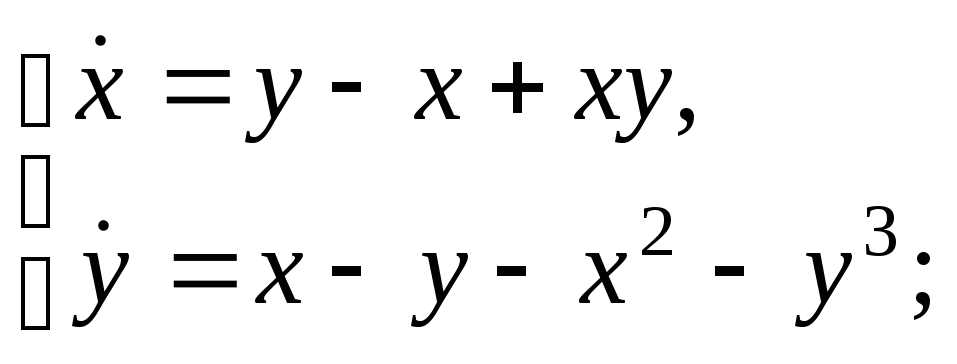 б)
б)
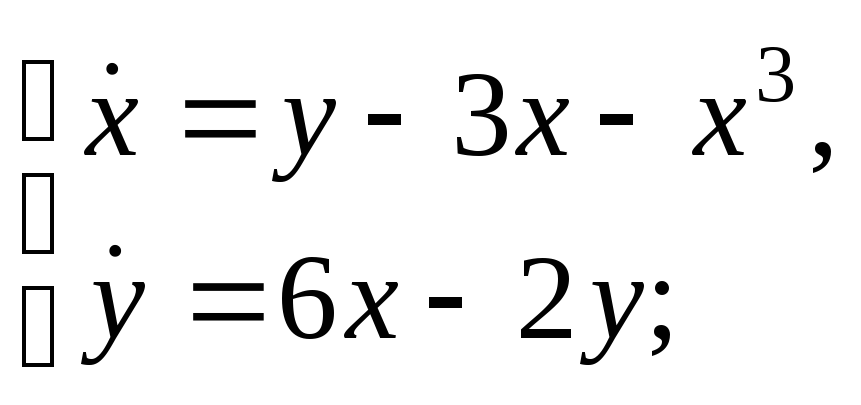 в)
в)
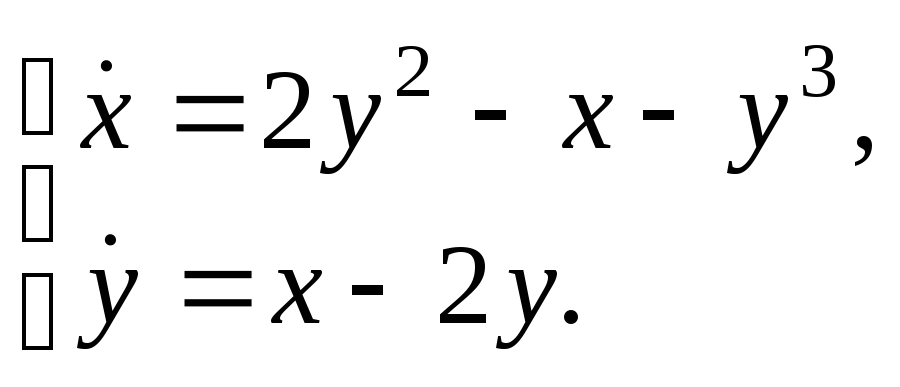
-
Выяснить, устойчиво ли решение системы:
а)
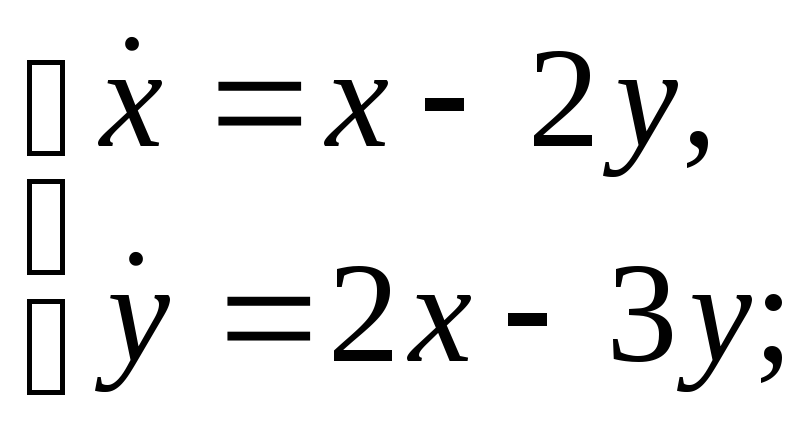 б)
б)
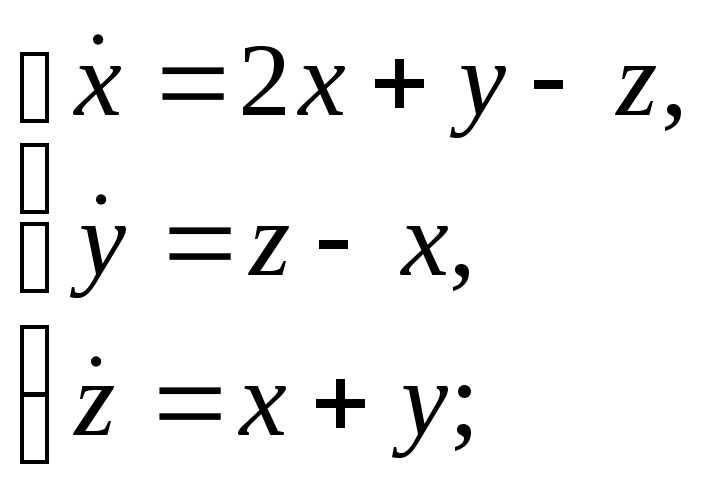 в)
в)
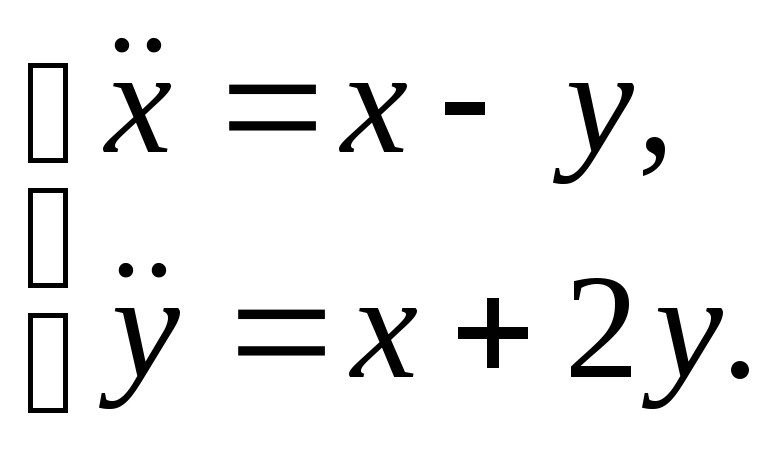
-
Найти наибольший интервал значений параметра
 при которых решения данных систем
устойчивы:
при которых решения данных систем
устойчивы:
а)
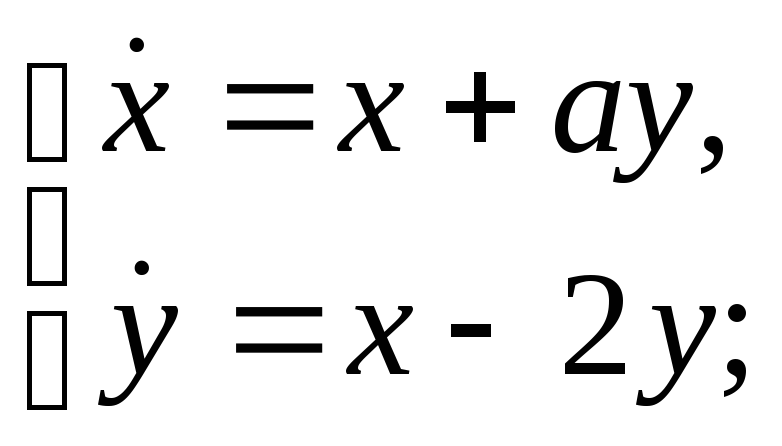 б)
б)

-
Применяя теорему об устойчивости по первому приближению, выяснить, устойчиво ли нулевое решение системы:
а)
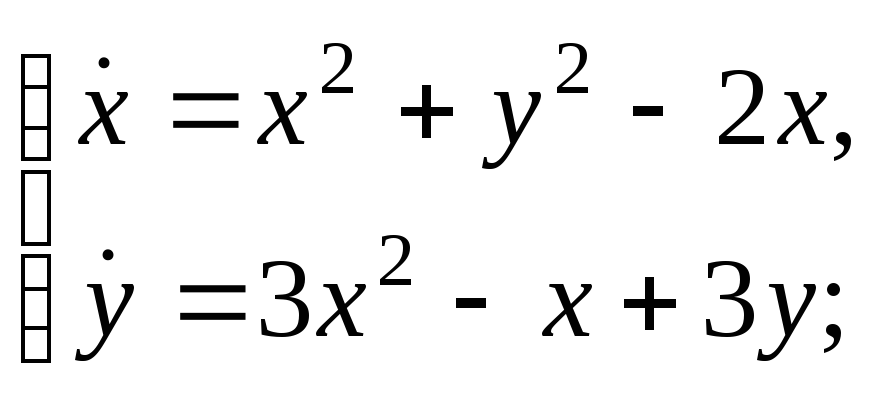 б)
б)
 в)
в)
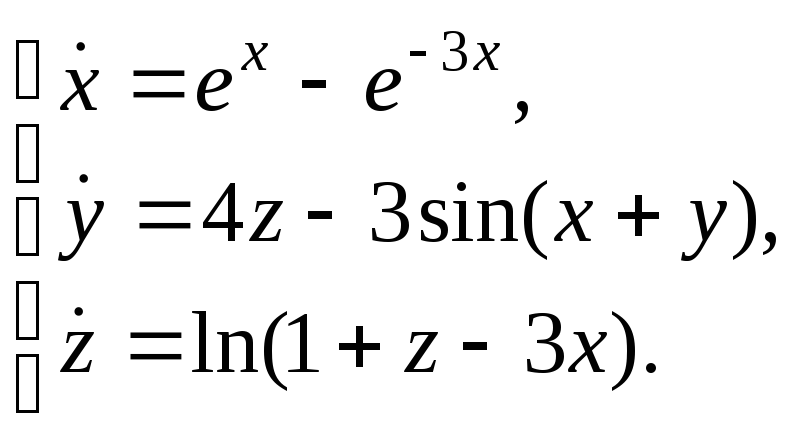
-
Выяснить, устойчиво ли нулевое решение уравнения:
а)
![]() б)
б)
![]()
Ответы:
1. а) Устойчиво; б) неустойчиво. 2. а)
![]()
б)
![]() (указание: искать функцию Ляпунова в
виде
(указание: искать функцию Ляпунова в
виде
![]() где
где
![]() в)
в)
![]() 3. а) Да; б) нет; в) нет. 4. а)
3. а) Да; б) нет; в) нет. 4. а)
![]() б)
б)
![]()
5. а) Нет; б) да; в) нет. 6. а) Да; б) нет.
