
Диф.уры Прокофьев / ГЛАВА2Б
.DOC§ 4. Уравнения в полных дифференциалах.
Интегрирующий множитель
Рассмотрим дифференциальное уравнение в симметричной форме:
![]() .
(1)
.
(1)
Если
бы оказалось, что левая часть этого
уравнения представляет полный дифференциал
некоторой функции
![]() ,
‑ в этом случае дифференциальное
уравнение называют уравнением в
полных дифференциалах:
,
‑ в этом случае дифференциальное
уравнение называют уравнением в
полных дифференциалах:
![]() ,
(2)
,
(2)
то,
зная функцию
![]() ,
мы получили бы общий интеграл уравнения
(1) в виде:
,
мы получили бы общий интеграл уравнения
(1) в виде:
![]() ,
(3)
,
(3)
ибо
из
![]() следует, что
следует, что
![]() .
.
Как установить, является ли дифференциальное
выражение
![]() полным дифференциалом некоторой функции,
и если это так, то как эту функцию найти?
полным дифференциалом некоторой функции,
и если это так, то как эту функцию найти?
Предположим, что функции
![]() и
и
![]() непрерывны и имеют непрерывные частные
производные
непрерывны и имеют непрерывные частные
производные
![]() и
и
![]() внутри некоторой области
внутри некоторой области
![]() .
Необходимым и достаточным условием
того, чтобы выражение
.
Необходимым и достаточным условием
того, чтобы выражение
![]() было полным дифференциалом, является
равенство частных производных:
было полным дифференциалом, является
равенство частных производных:
![]() =
=![]() (4)
(4)
Докажем
сначала необходимость условия (4). Если
![]() является полным дифференциалом функции
является полным дифференциалом функции
![]() ,
то это значит, что
,
то это значит, что
![]() ,
а
,
а
![]() .
Дифференцируя первое равенство по у,
а второе по х, получаем:
.
Дифференцируя первое равенство по у,
а второе по х, получаем:
![]() ,
,
![]()
Смешанные производные
![]() и
и
![]() ,
будучи непрерывными, как это предполагается
условием нашей теоремы, должны совпадать:
,
будучи непрерывными, как это предполагается
условием нашей теоремы, должны совпадать:
![]() =
=
![]() .
Отсюда следует равенство (4).
.
Отсюда следует равенство (4).
Предполагая теперь условие (4) выполненным,
мы покажем, что можно будет построить
такую функцию
![]() ,
которая своим полным дифференциалом
будет иметь
,
которая своим полным дифференциалом
будет иметь
![]() .
Такая функция
.
Такая функция
![]() ,
если она существует, должна иметь своими
производными по x и у функции
,
если она существует, должна иметь своими
производными по x и у функции
![]() и
и
![]() ,
соответственно:
,
соответственно:
![]() ,
,
![]() (5)
(5)
Из первого требования (5) следует, что
 ;
;
![]() (6)
(6)
поскольку
при интегрировании у рассматривается
как постоянная величина, произвольное
постоянное С(у) зависит от у,
представляя, таким образом, произвольную
функцию от у. При любом выборе этой
функции и предела интегрирования, точки
![]() ,
,
![]() .
Следовательно, первое из условий (5)
удовлетворено. Далее, функцией С(у)
мы постараемся распорядиться так, чтобы
удовлетворить и второму требованию
(5), чтобы, следовательно,
.
Следовательно, первое из условий (5)
удовлетворено. Далее, функцией С(у)
мы постараемся распорядиться так, чтобы
удовлетворить и второму требованию
(5), чтобы, следовательно,
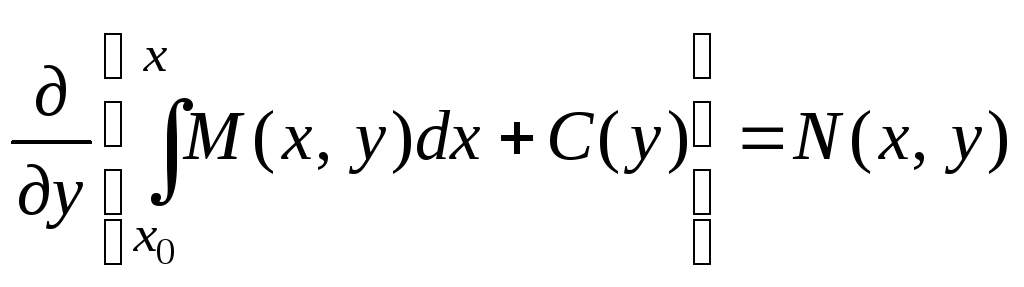 (7)
(7)
Выполняя дифференцирование под знаком интеграла и принимая во внимание условие (4), преобразуем левую часть уравнения (7) следующим образом:
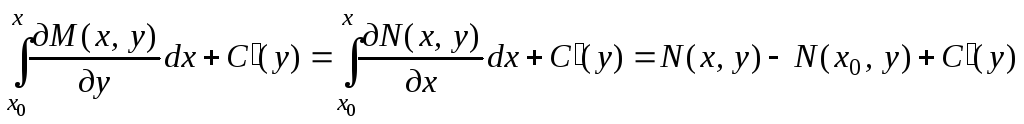 (8)
(8)
Отсюда видно, что, для того чтобы
выполнялось требование
![]() ,
надо, чтобы С'(у) = N(х0,
у). А это будет иметь место, если
положить:
,
надо, чтобы С'(у) = N(х0,
у). А это будет иметь место, если
положить:

(мы берем ту первообразную, которая при у=y0 обращается в нуль). Подставляя найденное выражение для С(у) в (6), мы получаем, что
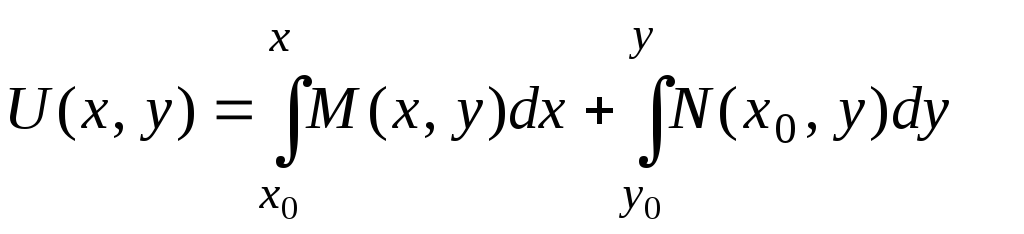 (9)
(9)
Таким
образом, не только доказано, что при
выполнении условия (4)
![]() есть полный дифференциал, но вместе с
тем найдена функция
есть полный дифференциал, но вместе с
тем найдена функция
![]() ,
полным дифференциалом которой является
,
полным дифференциалом которой является
![]() .
.
Приравнивая
![]() постоянной, согласно с (3) получаем общий
интеграл данного дифференциального
уравнения:
постоянной, согласно с (3) получаем общий
интеграл данного дифференциального
уравнения:
 (10)
(10)
который, как видим, выражается в квадратурах.
Установленный метод интегрирования,
таким образом, заключается в нахождении
функции
![]() по ее полному дифференциалу
по ее полному дифференциалу
![]() (такая функция
(такая функция
![]() называется первообразной, или
примитивной этого полного дифференциала).
Задача эта допускает неоднозначное
решение. Однако все функции, имеющие
один и тот же полный дифференциал,
отличаются на аддитивную постоянную:
если dU(х,
у) = dV(х, у), то
V(х,у)=U(х,у)+С. Для наших целей отыскания
общего интеграла дифференциального
уравнения безразлично, какую именно
первообразную взять, ибо общий интеграл
находится по формуле:
называется первообразной, или
примитивной этого полного дифференциала).
Задача эта допускает неоднозначное
решение. Однако все функции, имеющие
один и тот же полный дифференциал,
отличаются на аддитивную постоянную:
если dU(х,
у) = dV(х, у), то
V(х,у)=U(х,у)+С. Для наших целей отыскания
общего интеграла дифференциального
уравнения безразлично, какую именно
первообразную взять, ибо общий интеграл
находится по формуле:
![]() ,
,
где С
‑ произвольная постоянная. В
установленной нами формуле (10) за
первообразную взята такая функция
![]() ,
которая в точке
,
которая в точке
![]() обращается в нуль. Самую же точку
обращается в нуль. Самую же точку
![]() мы можем выбирать в Q
произвольно. Проще всего взять
мы можем выбирать в Q
произвольно. Проще всего взять
![]() ,
если только точка (0, 0) принадлежит
области Q, в которой непрерывны
функции дифференциалу
,
если только точка (0, 0) принадлежит
области Q, в которой непрерывны
функции дифференциалу
![]() ,
,
![]() и их производные
и их производные
![]() и
и
![]() .
.
Формула (10) не вполне симметрична: под
знаком первого интеграла стоит функция
![]() двух переменных, а под знаком второго
‑ функция
двух переменных, а под знаком второго
‑ функция
![]() одного переменного у. Если бы
построение функции
одного переменного у. Если бы
построение функции
![]() мы начали не с условия
мы начали не с условия
![]() ,
а с условия
,
а с условия
![]() ,
то пришли бы к общему интегралу:
,
то пришли бы к общему интегралу:
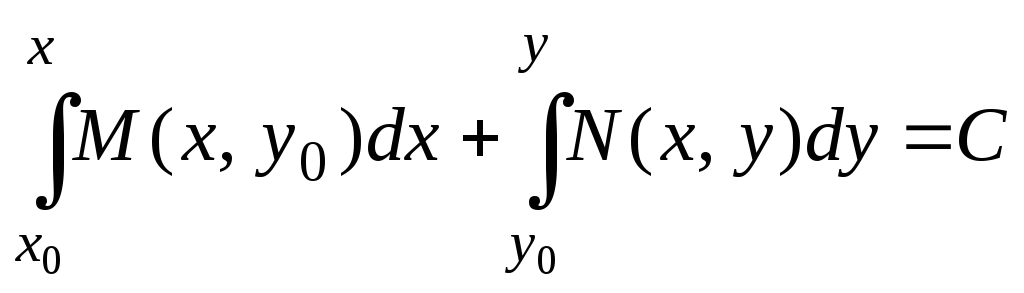 .
(11)
.
(11)
Справедливость этой формулы можно проверить непосредственно дифференцированием.
Частным случаем уравнения в полных дифференциалах является уравнение с разделенными переменными:
М(х)dx+N(у)dy=0,
к
которому приводится уравнение с
разделяющимися переменными после их
разделения. Действительно, в этом
![]() .
Решение может быть записано:
.
Решение может быть записано:
 ,
,
к которому в этом случае сводятся обе формулы (10) и (11).
При интегрировании уравнения в полных
дифференциалах можно обойтись и вовсе
без готовых формул, а искать функцию
![]() постепенно, пользуясь знанием ее частных
производных:
постепенно, пользуясь знанием ее частных
производных:
![]() ,
,
![]() .
(12)
.
(12)
Из первого равенства (12):
![]() .
.
Функцию С(у) далее подбираем так, чтобы удовлетворить и второму условию (12):
![]() .
.
Из этого уравнения находим С'(у), а по нему и С(у).
Возникает вопрос, будет ли решение уравнения в полных дифференциалах (1) при заданных начальных условиях единственным?
Докажем, что через любую точку
![]() внутри области Q
(в которой
внутри области Q
(в которой
![]() ,
,
![]() ,
,
![]() и
и
![]() непрерывны), если только в этой точке
не обращаются в нуль обе функции
непрерывны), если только в этой точке
не обращаются в нуль обе функции
![]() и
и
![]() ,
проходит единственная интегральная
кривая.
,
проходит единственная интегральная
кривая.
Частный
интеграл с начальными условиями
![]() получаем из (10), положив С=0:
получаем из (10), положив С=0:
![]() ,
(13)
,
(13)
где
![]() определяется формулой (9) (так
определяется формулой (9) (так
![]() ,
а
,
а
![]() ).
).
Положим,
что
![]() .
Тогда, так как
.
Тогда, так как
![]() ,
U(x,y) и
,
U(x,y) и
![]() непрерывны и
непрерывны и
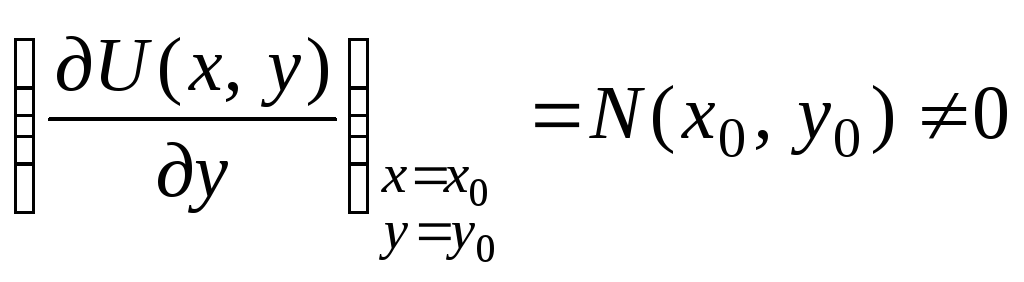 ,
т. е. выполнены условия теоремы о
неявной функции, можно утверждать, что
уравнение (13) определяет единственное
решение у=
,
т. е. выполнены условия теоремы о
неявной функции, можно утверждать, что
уравнение (13) определяет единственное
решение у=![]() (х),
такое, что
(х),
такое, что
![]() .
.
Покажем, что другого решения,
удовлетворяющего тем же начальным
условиям, у дифференциального уравнения
нет. Допустим противное. Пусть функция
![]() ,
такая, что
,
такая, что
![]() также является решением данного уравнения
(1), которое мы перепишем в виде:
также является решением данного уравнения
(1), которое мы перепишем в виде:
![]() .
.
Таким образом, по предположению:
![]() .
.
Составим
теперь функцию
![]() и найдем ее производную:
и найдем ее производную:
![]()
Так
как производная функции
![]() тождественно равна нулю, то функция эта
сохраняет постоянное значение ‑ то,
которое она имеет в точке
тождественно равна нулю, то функция эта
сохраняет постоянное значение ‑ то,
которое она имеет в точке
![]() :
:
![]() .
.
Видно, что функция
![]() удовлетворяет уравнению (13). А так как
у=
удовлетворяет уравнению (13). А так как
у=![]() (х)
также удовлетворяет этому уравнению и
(х)
также удовлетворяет этому уравнению и
![]() ,
то обе функции
,
то обе функции
![]() и у=
и у=![]() (х)
должны совпадать. Таким образом, решение
у=
(х)
должны совпадать. Таким образом, решение
у=![]() (х)
единственное.
(х)
единственное.
В случае, если
![]() ,
а
,
а
![]() ,
точно так же можно показать, что через
точку
,
точно так же можно показать, что через
точку
![]() проходит единственная интегральная
кривая вида:
проходит единственная интегральная
кривая вида:
![]() .
.
Полученные результаты можно сформулировать следующим образом:
Теорема. Уравнение
![]() при условии, что в области
Q:
при условии, что в области
Q:
1)
![]() ,
,![]() ,
,
![]() и
и
![]() непрерывны, 2)
непрерывны, 2)
![]() =
=![]()
и
3)
![]() и
и
![]() не обращаются одновременно в нуль, имеет
общий, интеграл, выражаемый в квадратурах,
причем начальными условиями
не обращаются одновременно в нуль, имеет
общий, интеграл, выражаемый в квадратурах,
причем начальными условиями
![]() ,
где
,
где
![]() ‑ любая точка области Q,
определяется единственное решение.
‑ любая точка области Q,
определяется единственное решение.
Точка
![]() ,
в которой одновременно
,
в которой одновременно
![]() и
и
![]() ,
очевидно является особой.
,
очевидно является особой.
Предположим, что дифференциальное
уравнение
![]() является одновременно однородным и
в полных дифференциалах. Каким методом
его предпочтительнее интегрировать?
Оказывается, что в этом случае (если
только степень его однородности
является одновременно однородным и
в полных дифференциалах. Каким методом
его предпочтительнее интегрировать?
Оказывается, что в этом случае (если
только степень его однородности
![]() )
общий интеграл находится вовсе без
квадратур, сразу по формуле:
)
общий интеграл находится вовсе без
квадратур, сразу по формуле:
![]() .
(14)
.
(14)
Докажем это. Поскольку
![]() и
и
![]() ‑ однородные функции степени k,
то по теореме Эйлера
‑ однородные функции степени k,
то по теореме Эйлера
![]() ;
;
![]() .
.
Кроме того, из условия следует, что
![]() =
=![]() .
Тогда
.
Тогда
![]()
![]() ;
;
![]()
![]() ;
;
Таким образом,
![]() .
.
и если
![]() ,
т. е.
,
т. е.
![]() ,
то общим интегралом данного уравнения,
очевидно, будет:
,
то общим интегралом данного уравнения,
очевидно, будет:
![]() .
.
Разбор типовых примеров
1.
![]()
Решение:
Необходимым условием того, чтобы
уравнение
![]() (раньше
оно обозначалось
(раньше
оно обозначалось
![]() )
было уравнением в полных дифференциалах,
является равенство
)
было уравнением в полных дифференциалах,
является равенство
![]()
Проверим его выполнимость:
![]()
![]()
![]()
Следовательно,
условие
![]() выполнимо и, значит,
выполнимо и, значит,
![]()
![]() (или
(или
![]() ).
Неизвестную функцию
).
Неизвестную функцию
![]() (или
(или
![]() )
найдем из условия
)
найдем из условия
![]() (или
(или
![]() ):
):

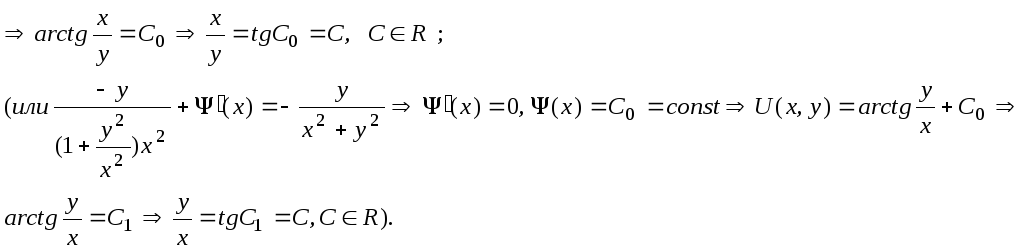
Полученное уравнение
![]() (или
(или
![]() ),
однако, не охватывает множества всех
решений данного дифференциального
уравнения, так как функции
),
однако, не охватывает множества всех
решений данного дифференциального
уравнения, так как функции
![]() и
и
![]() определены в области D,
представляющей собой плоскость с
выколотой точкой (0,0)
(х2+у20)
и не являющейся односвязной. В таком
случае условие
определены в области D,
представляющей собой плоскость с
выколотой точкой (0,0)
(х2+у20)
и не являющейся односвязной. В таком
случае условие
![]() не является достаточным, и те кривые,
лежащие в области Д,
на которых найденная функция не
определена, могут быть дополнительными
интегральными кривыми. В данном примере
это у=0 (или
х=0),
причем точка (0,
0)
устранена.
не является достаточным, и те кривые,
лежащие в области Д,
на которых найденная функция не
определена, могут быть дополнительными
интегральными кривыми. В данном примере
это у=0 (или
х=0),
причем точка (0,
0)
устранена.
Ответ:
![]() или
или
![]()
2.
![]()
Решение:
![]()
 Ответ:
Ответ:
![]()
3.
![]()
Решение:
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
4.
![]()
Решение:
![]()
![]() ,
,
![]()
![]()
![]()
Ответ:
![]()
5.
![]()
Решение:
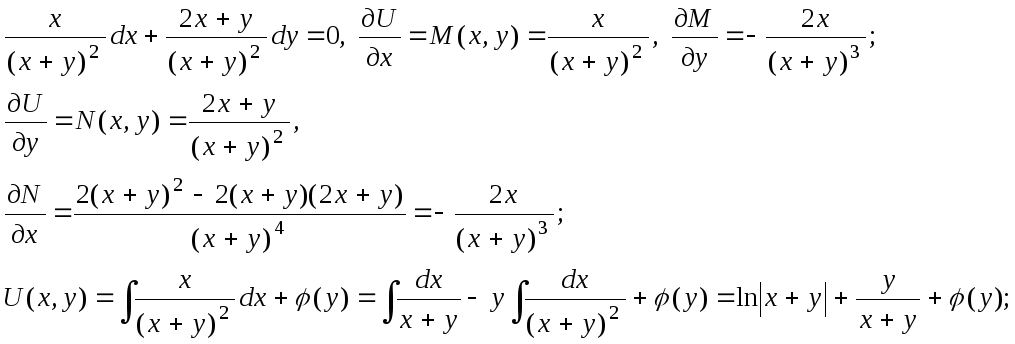
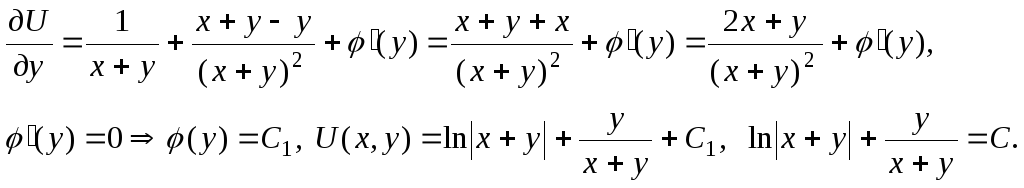
Ответ:
![]()
6.
![]()
Решение:
![]()
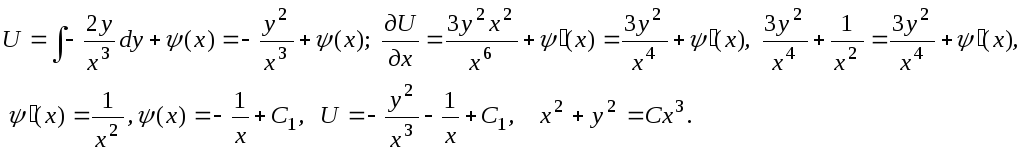 Ответ:
Ответ:
![]()
7.
![]() .
.
Решение:

![]()
![]()
![]()
![]()
Ответ:
![]()
8.
![]()
Решение:
![]()
![]()
![]()
![]()
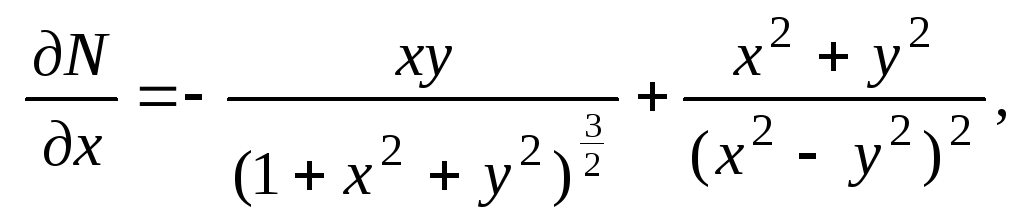
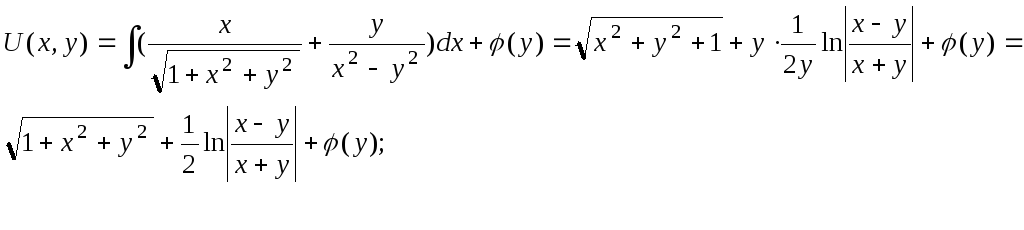
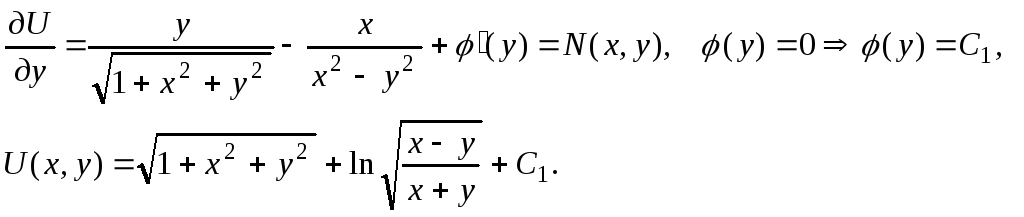
![]()
Ответ:
![]()
9.
![]()
Решение:
![]()
![]()
![]()
![]()
Ответ:
![]()
10.
![]()
Решение:
![]()
![]()
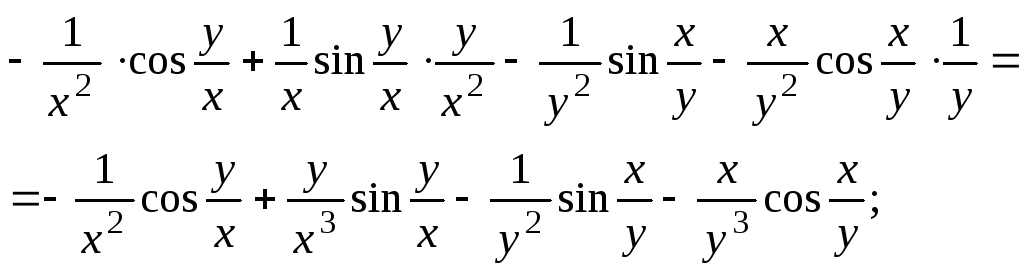
![]()
![]()
![]()
Ответ:
![]()
Задачи для самостоятельного решения
1.
![]() Ответ:
Ответ:
![]()
2.
![]() Ответ:
Ответ:
![]()
3.
![]() Ответ:
Ответ:
![]()
4.
![]() Ответ:
Ответ:
![]()
5.
![]() Ответ:
Ответ:
![]()
6. (х2у-1)у`+xy2=1. Ответ: x2y2-2(x+y)=C.
7.
![]() Ответ:
xy-ln(xy3)=C.
Ответ:
xy-ln(xy3)=C.
8. 2x3yy`+3x2y2+7=0. Ответ: x3y2+7x=C.
9. (y2-x)y`-y+x2=0. Ответ: x3 +y2-3xy=C.
10. (y2+x2+a)y`+2xy+x2+в=0. Ответ: x3 +y3+3(x2y+ау+вх)=C.
11.![]() Ответ:
Ответ:
![]()
12.![]() Ответ:
Ответ:
![]()
13. xy` cos y+sin y=0. Ответ: x sin y=C.
14. (x cos y+cos x)y`-y sin x+sin y=0. Ответ: x sin y+y cos x=C.
15. (x2cos y+2y sin x)y`+2x sin y+y2cos x=0. Ответ: x2sin y+y2sin x=C.
