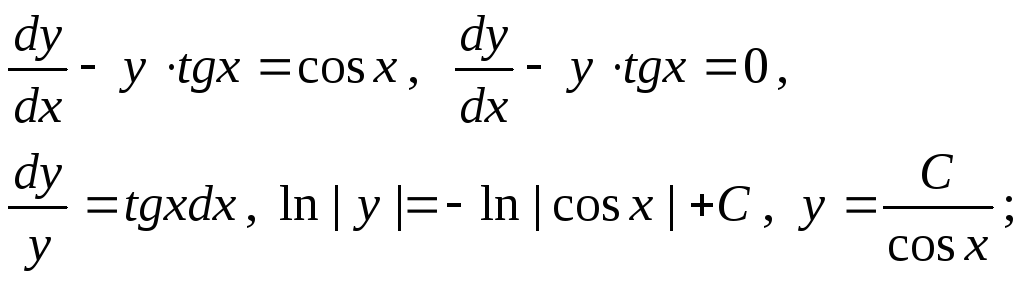Диф.уры Прокофьев / ГЛАВА2А
.DOC§ 3. Линейное уравнение
1.
Дифференциальное уравнение
,
разрешенное относительно производной,
называется линейным, если его правая
часть линейна, т. е. первой степени,
относительно у:
(1)
Уравнение это линейно как относительно функции у, так и относительно ее производной у'.
Положим,
что функции Р (х) и Q(x)
непрерывны в интервале
.
В этом случае, как будет показано, через
каждую точку полосы
проходит единственное решение данного
уравнения.
Рассмотрим сначала линейное однородное уравнение, соответствующее уравнению (I):
.
(2)
Мы
предполагаем, следовательно, что
свободный член
.
Уравнение (2) есть уравнение с разделяющимися
переменными. Разделяем переменные
и интегрируем:
или
(3)
Решение
,
не получаемое из (3), не является особым,
так как ни одна из показательных кривых
не пересекает оси Ox.
Условившись параметру в (3) приписывать
и значение, равное нулю, получаем
окончательно общее решение:
(4)
Решение, удовлетворяющее
начальным условиям
,
где
‑ любая точка области G,
может быть написано в виде:
Такое решение единственное.
Для
нахождения решения уравнения (1)
применим метод варьирования
постоянной: в общем решении (4) однородного
уравнения заменим постоянное С
функцией
:
(6)
При
этом
постараемся подобрать так, чтобы
удовлетворить неоднородному уравнению
(1). Мы увидим, что таких функций найдется
не одна, а множество (семейство, зависящее
от одного параметра). Дифференцируем
(6) и подставляем в данное уравнение (I):
.
Отсюда
и, следовательно,
.
(7)
Подставляя найденное выражение для С(х) в (6), получаем общее решение линейного уравнения:
.
(8)
Чтобы
получить решение с начальными условиями
,
нужно в решение (5) однородного уравнения
вместо
подставить такую определяемую соотношением
(7) функцию
,
которая при
принимала значение
.
Такая функция найдется только одна:
.
Подставляя в (6), находим искомое единственное решение:
.
(9)
Таким образом, доказано следующее предложение:
Теорема. Линейное дифференциальное уравнение
,
где Р(х) и
Q(x) ‑ функции, непрерывные
в интервале
,
имеет общее решение, выражаемое
в квадратурах; при этом через каждую
точку внутри полосы
G,
ограниченной прямыми х=а и
у=b, проходит,
единственная интегральная кривая этого
уравнения.
Таким образом, внутри полосы G, а если Р(х) и Q(x) всюду непрерывны, то во всей плоскости Oxу, линейное уравнение не имеет особых точек, а следовательно, и особых решении.
2. Если уравнение не разрешено относительно производной, то, чтобы установить его линейность, надо убедиться, что оно содержит у и у' в первой степени и не содержит их произведения. Чтобы пользоваться выведенной выше формулой (8). надо разрешить его относительно производной. Однако при интегрировании линейного уравнения (1) можно обойтись и без пользования готовой формулой, а искать решение в виде произведения:
,
(10)
где и и v ‑ функции от х, которые постараемся подобрать так, чтобы их произведение удовлетворило данному уравнению. Подставляя (10) в уравнение (1), получаем:
или
.
(*)
Функцию и выбираем так, чтобы
.
Для
этого нужно, чтобы
(мы берем одно из возможных значений
для u).При таком выборе
и соотношение (*) примет вид:
.
Отсюда
.
Произведение u на v и дает искомое решение.
3. Из формулы (8), дающей решение линейного уравнения, мы видим, что
,
т. е. общее решение линейного (неоднородного) уравнения есть сумма общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Впоследствии будет показано, что этим свойством обладают и линейные уравнения высшего порядка.
Из
предшествующего следует, что, зная одно
какое-нибудь частное решение неоднородного
уравнения и какое-либо частное решение
соответствующего однородного уравнения,
мы можем записать общее решение
неоднородного уравнения в виде:
.
(**)
Если
теперь
,
и
‑ два каких-либо частных решения
неоднородного уравнения, так что
и
,
то, вычитая, получаем:
.
Разность
оказывается, таким образом,
решением однородного уравнения. А потому
согласно (**) общее решение можно записать
в виде:
,
или
(***)
Таким образом, любое решение линейного неоднородного уравнения выражается линейной комбинацией вида (***) двух каких-либо его частных решений.
Разбор типовых примеров
1.
Решить уравнение
.
Решение:
|
Первый способ
|
второй способ
|
Ответ:
2.
Решить уравнение
Решение:
,
Ответ:
3.
Решить уравнение
Решение:
,
,
,
,
Ответ:
4.
Решить уравнение
Решение:
.
Ответ:
5.
Решить уравнение
Решение:
Ответ:
6.
Решить уравнение
.
Решение:
Ответ:
7.
Решить уравнение
.
Решение:
Ответ:
8.
Решить уравнение
.
Решение:
Ответ:
9.
Решить уравнение
Решение:
Ответ:
10.
Решить уравнение
Решение:
Ответ:
11.
Решить уравнение
.
Решение:
,
Ответ:
12. Решить
уравнение
Решение:
Ответ:
13.
Решить уравнение
Решение:
Ответ:
14.
Решить уравнение
Решение:
Ответ:
15. Решить
уравнение
Решение:
y=Cx,
,
Ответ:
Задачи для самостоятельного решения
Решить уравнения:
1.
Ответ:
2.
.
Ответ:
3.
.
Ответ:
.
4.
.
Ответ:
.
5.
.
Ответ:
x =Cey
- y2
- 2y - 2 .
6.
Ответ:
.
7.
Ответ:
.
8.
Ответ:
.
9.
Ответ:
10.
Ответ:
11.
Ответ:
.
12.
Ответ:
13.
Ответ:
14.
Ответ:
15.
Ответ:
16.
Ответ:
17.
Ответ:
18.
Ответ:
19.
Ответ:
20.
Ответ:
21.
Ответ:
22.
Ответ:
23.
Ответ:
24.
Ответ:
25.
Ответ:
26.
Ответ:
27.
Ответ:
28.
Ответ:
29.
Ответ:
Указание:
30.
Ответ:
Указание:
Уравнение Бернулли
К линейному уравнению может быть приведено уравнение:
,
называемое уравнением
Бернулли. Показатель т может
быть любым числом; но при
получаем линейное уравнение, а при
‑ уравнение с разделяющимися
переменными; поэтому считаем, что
.
Делим
на
,
или, что то же, умножаем на
:
.
Вводя
подстановку
и, следовательно,
,
приходим к линейному уравнению:
.
Находя его решение по формуле (8), получаем общий интеграл данного уравнения (12):
.
Таким
образом, уравнение Бернулли также
интегрируется в квадратурах. Помимо
общего интеграла (11), данное уравнение
при m >0
имеет еще очевидное решение у =
0, не получаемое из общего. (Решение это
не могло получиться из общего потому,
что при выводе последнего мы делили на
и потому предполагали, что
.)
При
решении уравнения Бернулли нет
необходимости пользоваться готовой
формулой (11); проще подстановкой
превратить его в линейное уравнение.
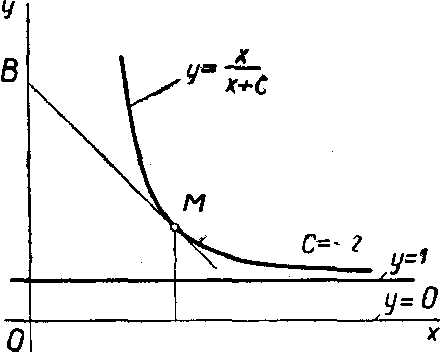
Задача. Найти кривые, у которых отрезок, отсекаемый касательной на оси Oy, равен квадрату ординаты точки касания.
Решение. Таким образом, условие задачи требует, чтобы (рис. 1)
.
Отрезок
находим из уравнения касательной:
,
положив в нем
;
тогда
.
Дифференциальное
уравнение задачи, таким образом, будет:
Разрешая
его относительно у':
,
видим, что это уравнение Бернулли.
Рис. 1.
Деля на у2 и полагая
,
откуда
,
приходим к линейному уравнению:
.
(а)
Обозначая
,
получим
;
.
Замечая,
что
,
получаем:
,
или
.
Искомые
кривые ‑ гиперболы и (при
)
прямая
.
Кроме того, решением является также
прямая
.
Решение типовых примеров
1. Решить
уравнение
Решение:
0 ,
следовательно,
есть тривиальное решение у = 0.
Делим обе части данного уравнения на
:
Делаем замену
,
и подставляем в последнее уравнение:
(линейное
уравнение).
Ответ:
2. Решить
уравнение
Решение:
Ответ:
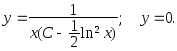
3. Решить
уравнение
Решение:
,
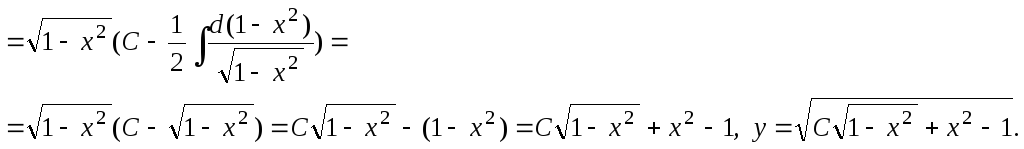
Ответ:
4.
Решить уравнение
Решение:
,
