Глава 3. Существование и единственность решения дифференциального уравнения

Предположим, что при решении какой-либо физической или инженерной задачи у нас получилось дифференциальное уравнение. Если оно относится к одному из типов, метод решения которого был изложен ранее (например, если оно линейное первого порядка, или с разделяющимися переменными, или в полных дифференциалах), то препятствий для получения аналитического решения этого уравнения нет (под аналитическим решением мы понимаем формулу, выражающую искомую функцию через элементарные функции или интегралы от элементарных функций). Однако, далеко не всегда дифференциальное уравнение может быть решено аналитически. Тогда можно попытаться решить это уравнение приближённо, т.е. построить функцию (выраженную формулой, или таблицей, или графиком), в том или ином смысле близкую к точному решению. Но для этого мы должны быть уверены, что точное решение существует.

Теперь предположим, что каким-либо образом удалось найти решение дифференциального уравнения. Тогда возникает вопрос: а является ли это решение тем, которое мы искали, т.е. действительно ли оно описывает данный процесс? Если уравнение имеет более одного решения, то, может быть, мы нашли не то решение, которое требовалось найти. Таким образом, мы должны быть уверены, что решение дифференциального уравнения единственно.

И действительно, при определённых условиях на функцию уравнение

(1)

имеет решение, удовлетворяющее начальному условию и это решениеединственно. Точная формулировка этого утверждения даётся теоремой существования и единственности, формулировка которой будет приведена позже. Прежде, чем переходить к этой теореме, нам надо познакомиться с элементами теории метрических пространств.

1. Метрические пространства

Определение. Множество Х называется метрическим пространством, если любым двум элементам поставлено в соответствие действительное число(называемоерасстоянием между х и у) такое, что выполняются аксиомы:

(М1) причём

(М2) (симметричность);

(М3) (неравенство треугольника).

Функция называетсяметрикой.

Приведём примеры метрических пространств.

1. Произвольное множество Х можно сделать метрическим пространством, если положить

Это пространство называется дискретным.

2. Множество R действительных чисел является метрическим пространством относительно обычной метрики

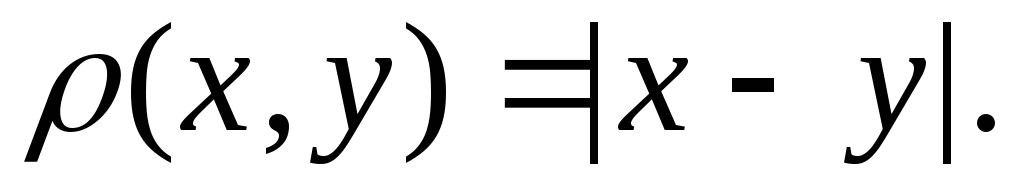
3. Множество 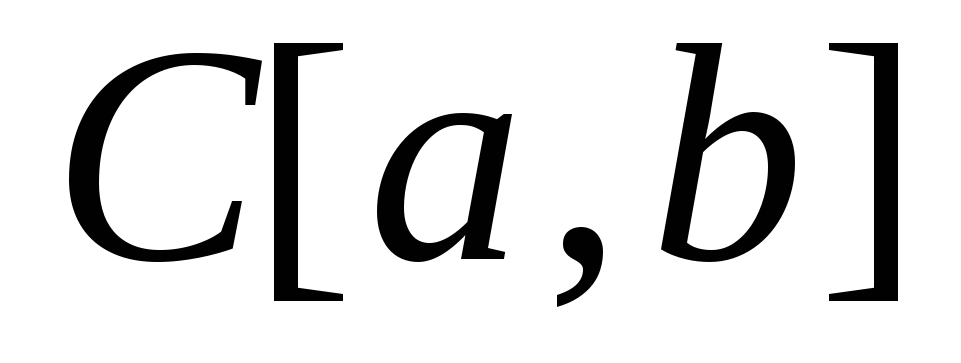всех функций, определённых на отрезке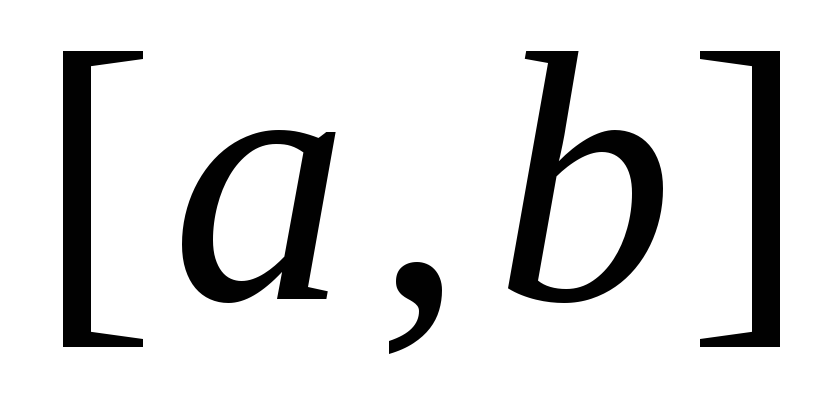и непрерывных на этом отрезке, является метрическим пространством относительноравномерной метрики

(2)

Докажем это. Неравенство очевидно. Также ясно, чтоиНеочевидно лишь неравенство треугольника. ПустьПоложимТогдаипри всехСледовательно, для всехх из этого промежутка мы имеем:

Поэтому т.е.

4. Множество всех функций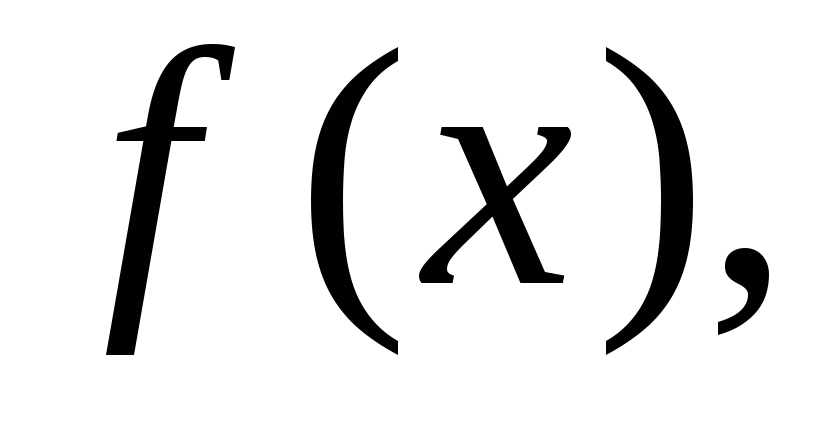для которых существуета расстояние в котором определяется по формуле

(3)

метрическим пространством не является, так как в нём не выполнена аксиома (М1): действительно, если при всехафункция, равная 0 прии 1 притоаЭту ситуацию можно исправить, отождествляя такие функциидля которыхт.е. считая такие функции одним элементом пространстваТогдабудет метрическим пространством. Расстояние, определяемое по формуле (3), называетсяинтегральной метрикой.

5. Множество всех функцийдля которых существуетявляется метрическим пространством относительно метрики

(4)

если считать функции идля которыходним и тем же элементом пространства

6. Множество R(п-мерное линейное пространство над полем действительных чисел), как и всякое бесконечное множество, можно превратить в метрическое пространство многими способами. Наиболее употребительными являются следующие метрики на R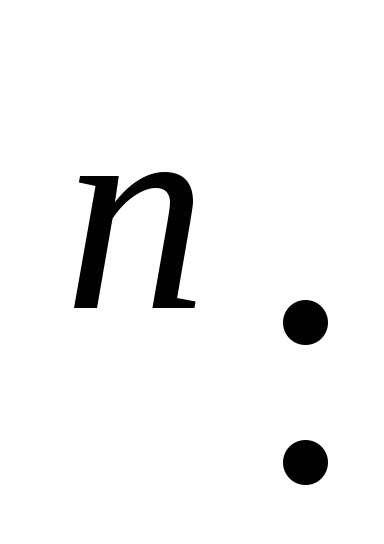

(5)

(6)

(7)

где RОбычно вRиспользуется метрика

7. Множество С комплексных чисел является метрическим пространством относительно метрики Это пространствоизометрично пространству Rв том смысле, что существует взаимно однозначное соответствие между элементами этих пространств, сохраняющее расстояния между любыми двумя точками.

Более узким, чем метрическое пространство, является понятие нормированного пространства.

Определение.Пустьлинейное пространство над полемRилиСназываетсянормированным пространством, если каждому векторупоставлено в соответствие действительное число(называемоенормойэлементах) так, что выполняются следующие аксиомы:

(Н1) причём

(Н2) для любого и любогоR(илиС)

(Н3) для любых

Всякое нормированное пространство является метрическим, а именно, расстояние в нём можно определить по формуле

(8)

Аксиомы (М1)-(М3) следуют в этом случае из (Н1)-(Н3). Метрические пространства из примеров 2,3,4,5,6,7 являются нормированными, а дискретное пространство (пример 1) нормированным не является. Нормы, определяющие метрики из примера 6, имеют вид:

(9)

(10)

(11)

Замечания. 1) п-мерное комплексное линейное пространство Стакже может рассматриваться как нормированное (а значит, и метрическое) пространство; норма в нём определяется формулой

(12)

где Са С.

2) Через у нас было обозначено пространство всех непрерывных на отрезкедействительных функцийОднако, можно рассматривать также комплекснозначные функциидействительного аргументах, т.е. функций вида гдеR. Множество таких функций будем также обозначать через Норма в этом пространстве определяется такой же формулой, как и в действительном случае:

разница лишь в том, что теперь обозначает модуль (абсолютную величину) комплексного числа.