
- •Глава 3. Существование и единственность решения дифференциального уравнения
- •1. Метрические пространства
- •Типовые задачи
- •Задачи для самостоятельного решения
- •Полные пространства
- •Типовые задачи
- •Задачи для самостоятельного решения
- •3. Принцип сжимающих отображений
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6. Теорема существования и единственности для линейных уравнений и систем
Примеры решения задач
Привести формулировку теоремы существования и единственности решения системы дифференциальных уравнений
 (28)
(28)
с начальным условием
![]()
![]() (29)
(29)
Решение.
Здесь система уравнений рассматривается
в области![]() Следовательно, если вектор-функция
Следовательно, если вектор-функция![]() в области
в области![]() непрерывна похи удовлетворяет
условию Липшица по
непрерывна похи удовлетворяет
условию Липшица по![]() то точка
то точка![]() имеет окрестность
имеет окрестность![]()
![]()
![]() в которой решение системы (28) с начальным
условием (29) существует и единственно.
в которой решение системы (28) с начальным
условием (29) существует и единственно.
Указать какой-нибудь отрезок, на котором существует единственное решение системы

![]()
![]()
Решение.
Систему дифференциальных уравнений
можно переписать в виде![]() Проинтегрировав это векторное
равенство, мы получим:
Проинтегрировав это векторное
равенство, мы получим:
![]()
Пусть
![]() параллелепипед в пространстве
параллелепипед в пространстве![]() определяемый неравенствами
определяемый неравенствами![]()
![]()
![]() и пусть
и пусть![]() решение системы, определённое на
решение системы, определённое на![]() Тогда
Тогда![]()
![]() а значит,
а значит,![]() Возможные значения
Возможные значения![]() найдутся теперь из условия
найдутся теперь из условия![]() Последнее неравенство равносильно
следующему:
Последнее неравенство равносильно
следующему:![]() Чтобы нашлось число
Чтобы нашлось число![]() удовлетворяющее этому неравенству,
необходимо и достаточно, чтобы дискриминант
был больше или равен нулю. Таким образом,
удовлетворяющее этому неравенству,
необходимо и достаточно, чтобы дискриминант
был больше или равен нулю. Таким образом,![]() т.е.
т.е.![]() Следовательно, можно утверждать, что
на отрезке
Следовательно, можно утверждать, что
на отрезке![]() решение системы существует и единственно.
решение системы существует и единственно.
Даны две непрерывные функции
 и
и Могут ли кривые, изображённые на рисунке,
быть интегральными кривыми уравнения:
а)
Могут ли кривые, изображённые на рисунке,
быть интегральными кривыми уравнения:
а) б)
б)
Р ешение.
Обозначим точку пересечения кривых
через
ешение.
Обозначим точку пересечения кривых
через![]() Кривые на рисунке не могут быть
интегральными кривыми уравнения
Кривые на рисунке не могут быть
интегральными кривыми уравнения![]() так
как это противоречит теореме существования
и единственности решения. Иначе обстоит
дело с уравнением
так
как это противоречит теореме существования
и единственности решения. Иначе обстоит
дело с уравнением![]() Здесь теорема существования и
единственности утверждает единственность
решения, удовлетворяющего двум условиям:
Здесь теорема существования и
единственности утверждает единственность
решения, удовлетворяющего двум условиям:![]()
![]() Для кривых, изображённых на рисунке,
Для кривых, изображённых на рисунке,![]() имеет разные значения, и эти кривые
могут являться интегральными кривыми
рассматриваемого уравнения второго
порядка.
имеет разные значения, и эти кривые
могут являться интегральными кривыми
рассматриваемого уравнения второго
порядка.
Задачи для самостоятельного решения
При каких
 на отрезке
на отрезке существует решение системы
существует решение системы

удовлетворяющее
начальному условию
![]()
2. Сколько
существует решений уравнения
![]() удовлетворяющее одновременно двум
условиям:
удовлетворяющее одновременно двум
условиям:![]()
![]() если: а)
если: а)![]() б)
б)![]() в)
в)![]()
3.
Указать какой-нибудь отрезок, на котором
существует единственное решение
уравнения
![]() с начальным условием
с начальным условием![]()
![]()
М
 огут
ли кривые, изображённые на рисунке,
являться интегральными кривыми
уравнения: а)
огут
ли кривые, изображённые на рисунке,
являться интегральными кривыми
уравнения: а) б)
б)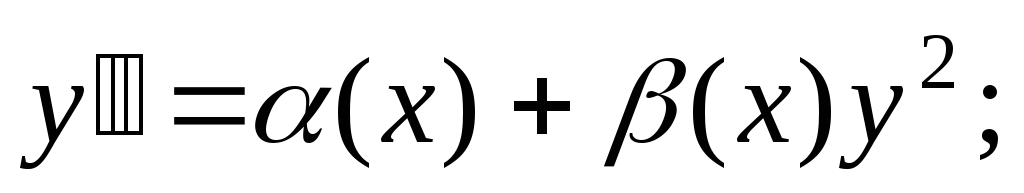 в)
в) если
если непрерывные функции?
непрерывные функции?
Ответы:1. При всех![]() 2. а) Ни одного, б) одно, в) бесконечно
много. 3.
2. а) Ни одного, б) одно, в) бесконечно
много. 3.![]() 4. а) Нет, б) нет, в) да.
4. а) Нет, б) нет, в) да.
6. Теорема существования и единственности для линейных уравнений и систем
Система линейных дифференциальных уравнений первого порядка имеет вид
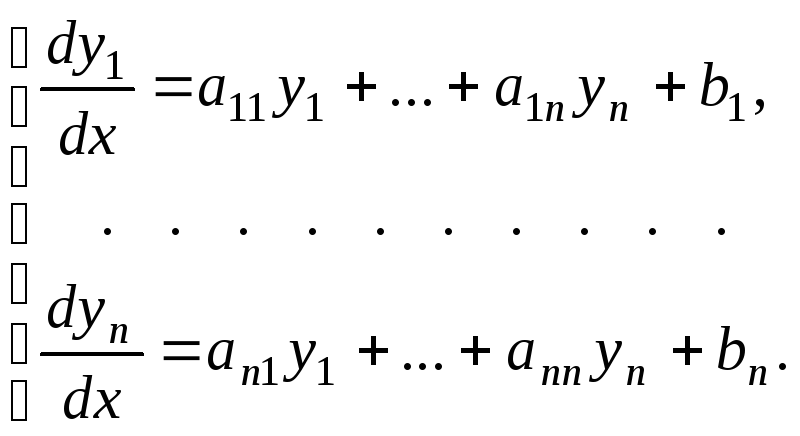 (30)
(30)
Здесь
![]() неизвестные функции (искомые), а
неизвестные функции (искомые), а![]() известные функции, которые мы будем
предполагать непрерывными на отрезке
известные функции, которые мы будем
предполагать непрерывными на отрезке![]() числовой прямой. Используя векторные
и матричные обозначения, систему (30)
можно переписать так:
числовой прямой. Используя векторные
и матричные обозначения, систему (30)
можно переписать так:
![]() (31)
(31)
где
![]() столбец из неизвестных функций, а
столбец из неизвестных функций, а![]() из известных. Требуется найти решение
системы, удовлетворяющее начальному
условию
из известных. Требуется найти решение
системы, удовлетворяющее начальному
условию![]()
Заметим,
что система (31) является частным случаем
более общей системы
![]() рассмотренной в предыдущем параграфе.
А именно, у линейной системы правая
часть представляет собой линейную
функцию от
рассмотренной в предыдущем параграфе.
А именно, у линейной системы правая
часть представляет собой линейную
функцию от![]()
![]() Вектор-функция
Вектор-функция![]() определена для
определена для![]() и любых
и любых![]() следовательно,
область
следовательно,
область![]() для линейной системы представляет собой
часть пространства
для линейной системы представляет собой
часть пространства![]() ограниченную двумя плоскостями
ограниченную двумя плоскостями![]() и
и![]() (см. рисунок).
(см. рисунок).

Далее
будет доказано, что, в отличие от
произвольных систем дифференциальных
уравнений, для линейных систем можно
гарантировать существование решения
на всём отрезке![]() а не только на маленьком промежутке
а не только на маленьком промежутке![]() Геометрически это означает, что через
каждую точку
Геометрически это означает, что через
каждую точку![]() проходит интегральная кривая, которая
одним концом“упирается”в плоскость
проходит интегральная кривая, которая
одним концом“упирается”в плоскость![]() а другим – в плоскость
а другим – в плоскость![]() (т.е. интегральные кривые“не
уходят в бесконечность”).
Сформулируем и докажем это утверждение.
(т.е. интегральные кривые“не
уходят в бесконечность”).
Сформулируем и докажем это утверждение.
Теорема
существования и единственности решения
линейной системы.Пусть дана линейная
система![]() где
где![]()
![]() матрица и столбец, состоящие из непрерывных
на
матрица и столбец, состоящие из непрерывных
на![]() функций. Тогда для каждого
функций. Тогда для каждого![]() и любого вектора
и любого вектора![]() существует решение системы, определённое
на всём отрезке
существует решение системы, определённое
на всём отрезке![]() и это решение единственно.
и это решение единственно.
Доказательство.
Единственность следует из теоремы
для произвольных систем, поэтому надо
доказать лишь существование решения
на всём отрезке![]() Для этого будем использовать метод
последовательных приближений. Построим
последовательность вектор-функций
Для этого будем использовать метод
последовательных приближений. Построим
последовательность вектор-функций
![]()

![]()
Так как
компоненты матрицы
![]() являются непрерывными функциями на
отрезке
являются непрерывными функциями на
отрезке![]() то они ограничены. Поэтому существует
константа
то они ограничены. Поэтому существует
константа![]() такая, что
такая, что![]() для всех
для всех![]() и любого вектора
и любого вектора![]() Оценим разности двух соседних членов
последовательности
Оценим разности двух соседних членов
последовательности![]() Для этого положим
Для этого положим![]() Теперь получаем:
Теперь получаем:
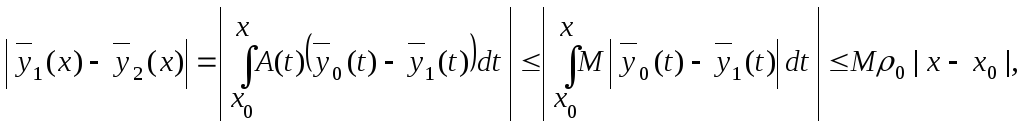
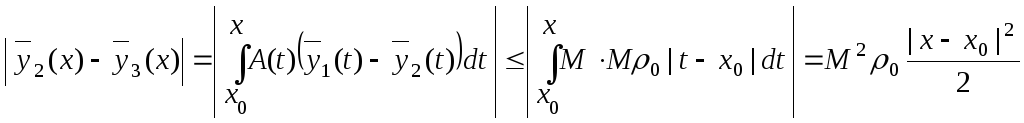 и
т.д., т.е.
и
т.д., т.е.![]() Отсюда следует, что для любых
Отсюда следует, что для любых![]()
![]()
![]() Положим
Положим![]() Тогда
Тогда
 Очевидно,
Очевидно,![]() при
при![]() поэтому последовательность
поэтому последовательность![]() фундаментальна, а значит, равномерно
сходится на отрезке
фундаментальна, а значит, равномерно
сходится на отрезке![]() Предельная функция этой последовательности,
очевидно, является решением дифференциального
уравнения.
Предельная функция этой последовательности,
очевидно, является решением дифференциального
уравнения.
Наконец, сформулируем теорему существования и единственности решения линейного уравнения п-го порядка, которая является непосредственным следствием только что доказанной теоремы.
Теорема существования и единственности решения линейного уравнения.Пусть дано линейное дифференциальное уравнение
![]() (32)
(32)
где
![]() и
и![]() непрерывные на отрезке
непрерывные на отрезке![]() функции. Тогда для каждого числа
функции. Тогда для каждого числа![]() и любой точки
и любой точки![]() существует решение
существует решение![]() уравнения (32), определённое на отрезке
уравнения (32), определённое на отрезке![]() и удовлетворяющее начальным условиям
и удовлетворяющее начальным условиям![]()
![]()
