
- •Глава 3. Существование и единственность решения дифференциального уравнения
- •1. Метрические пространства
- •Типовые задачи
- •Задачи для самостоятельного решения
- •Полные пространства
- •Типовые задачи
- •Задачи для самостоятельного решения
- •3. Принцип сжимающих отображений
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6. Теорема существования и единственности для линейных уравнений и систем
Примеры решения задач
Найти решение уравнения
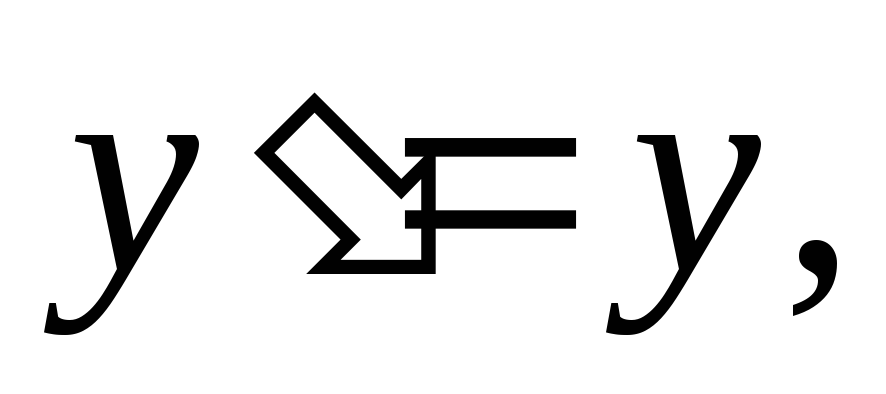 удовлетворяющее начальному условию
удовлетворяющее начальному условию методом последовательного приближения.
методом последовательного приближения.
Решение.
Разумеется, данное уравнение можно
решить достаточно просто другими
методами. Решим его методом последовательных
приближений, чтобы продемонстрировать
этот метод и убедиться в том, что он даёт
правильное решение. Последовательные
приближения к истинному решению имеют
вид:
![]()
![]()
![]() и т.д. Нетрудно видеть, что для любогоп
мы имеем
и т.д. Нетрудно видеть, что для любогоп
мы имеем
![]() Ясно, что на любом конечном отрезке
Ясно, что на любом конечном отрезке![]() числовой прямой
числовой прямой![]() Следовательно,
Следовательно,![]() искомая функция.
искомая функция.
Доказать, что решение уравнения
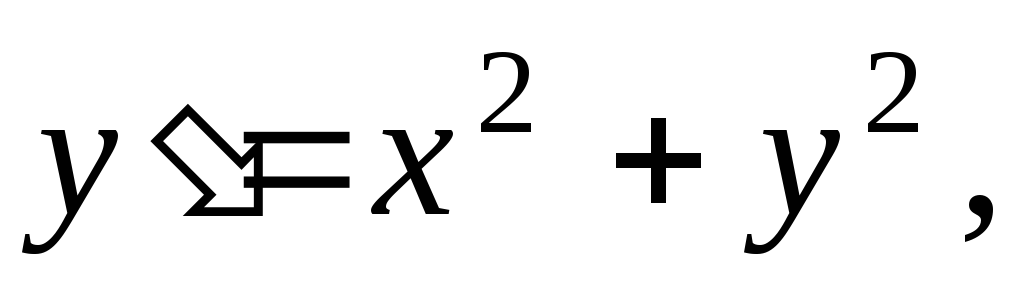 удовлетворяющее условию
удовлетворяющее условию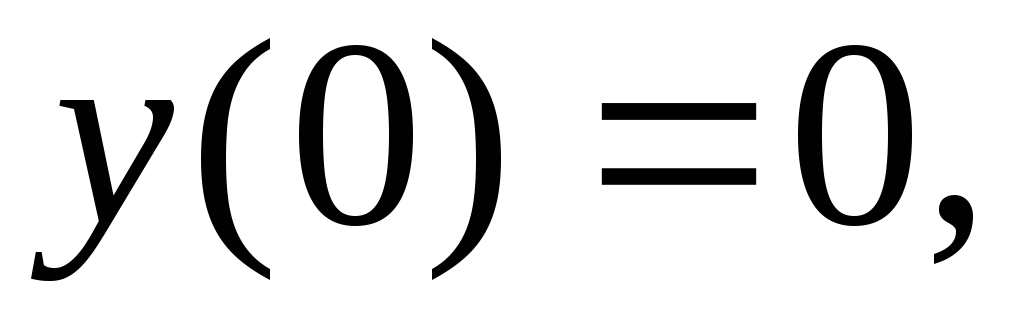 существует на отрезке
существует на отрезке но не продолжается на отрезок
но не продолжается на отрезок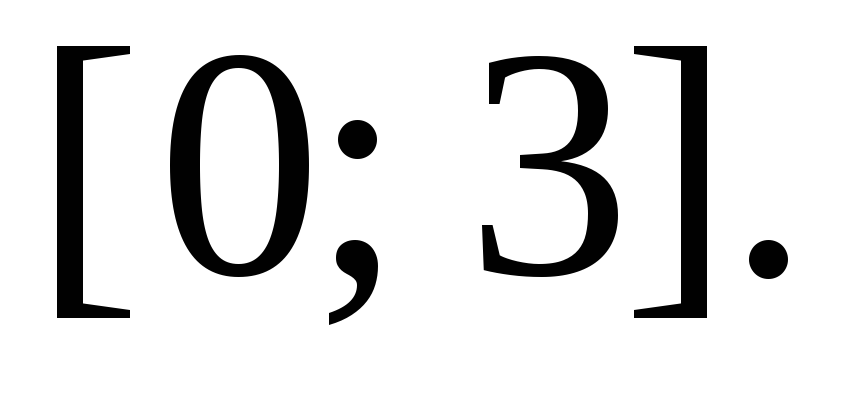
Доказательство.
Пусть
![]() решение уравнения
решение уравнения![]() определённое на отрезке
определённое на отрезке![]() и удовлетворяющее начальному условию
и удовлетворяющее начальному условию![]() Так как
Так как![]() то
то![]() при
при![]() поэтому
поэтому![]() возрастающая функция. Пусть
возрастающая функция. Пусть![]() при
при![]() Тогда
Тогда![]() Если
Если![]() и
и![]() таковы, что
таковы, что![]() то решение
то решение![]() существует на отрезке
существует на отрезке![]() В частности, при
В частности, при![]()
![]() мы имеем:
мы имеем:![]() поэтому уравнение имеет решение,
определённое на отрезке
поэтому уравнение имеет решение,
определённое на отрезке![]()
Займёмся
теперь отрезком
![]() Понятно, что если решение уравнения
Понятно, что если решение уравнения![]() не существует на отрезке
не существует на отрезке![]() то оно не существует и на отрезке
то оно не существует и на отрезке![]() Предположим теперь, что на отрезке
Предположим теперь, что на отрезке![]() решение существует. При
решение существует. При![]() мы имеем
мы имеем![]() поэтому
поэтому![]() Проинтегрировав это неравенство, мы
получим:
Проинтегрировав это неравенство, мы
получим:![]() откуда следует, что
откуда следует, что![]() т.е.
т.е.
![]() (23)
(23)
Так
как
![]() то
то![]() Если
Если![]() то
то![]() будет иметь на отрезке
будет иметь на отрезке![]() бесконечный разрыв, и неравенство (23)
для непрерывной функции
бесконечный разрыв, и неравенство (23)
для непрерывной функции![]() выполняться не будет. Таким образом,
выполняться не будет. Таким образом,![]() и
и![]() Значит, на отрезке
Значит, на отрезке![]() решений нет.
решений нет.
Продолжается ли на всю полуось
 решение уравнения
решение уравнения с начальным условием
с начальным условием
Решение.
Если
![]() решение
данного уравнения на отрезке
решение
данного уравнения на отрезке![]() то
то![]() Следовательно, на любом отрезке
Следовательно, на любом отрезке![]() где
где![]() решение уравнения существует. Значит,
оно продолжается на всю полуось
решение уравнения существует. Значит,
оно продолжается на всю полуось![]()
Пусть
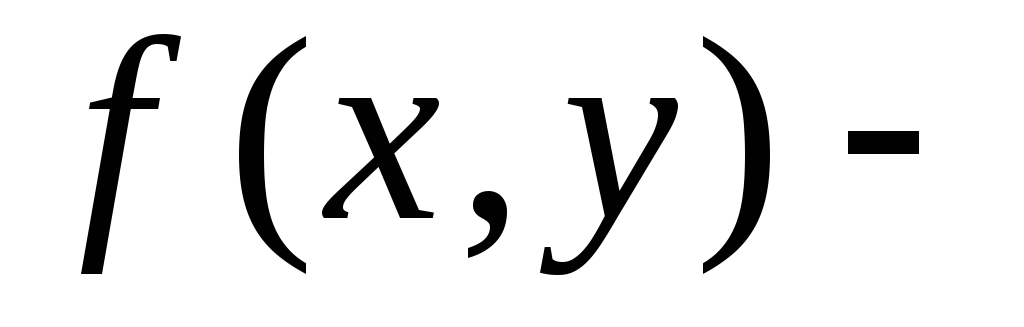 функция, определённая во всей плоскостиR
функция, определённая во всей плоскостиR и имеющая непрерывные производные в
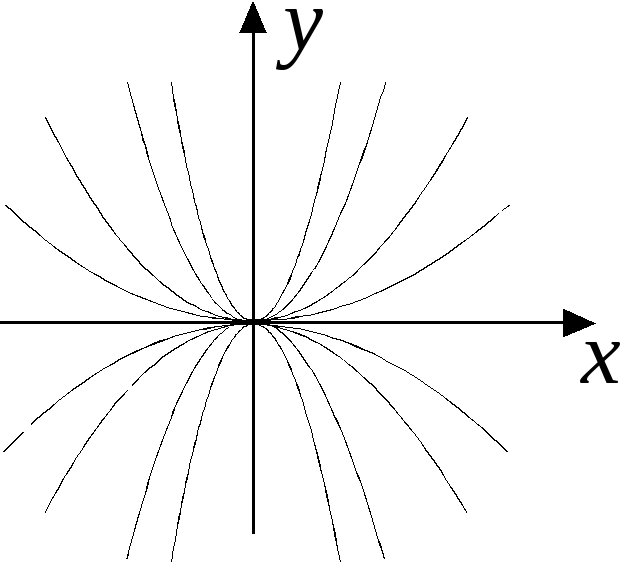
каждой точке плоскости. Может ли
семейство интегральных кривых уравнения
и имеющая непрерывные производные в
каждой точке плоскости. Может ли
семейство интегральных кривых уравнения иметь вид, изображённый на рисунке?
иметь вид, изображённый на рисунке?
Решение.
Так как функция
![]() имеет непрерывную производную по
имеет непрерывную производную по![]() то она удовлетворяет условию Липшица
по
то она удовлетворяет условию Липшица
по![]() Значит, через каждую тоску плоскости
проходит одна интегральная кривая
уравнения. Однако, на рисунке через
начало координат проходит более одной
интегральной кривой. Следовательно,
интегральные кривые уравнения изображены
неверно.
Значит, через каждую тоску плоскости
проходит одна интегральная кривая
уравнения. Однако, на рисунке через
начало координат проходит более одной
интегральной кривой. Следовательно,
интегральные кривые уравнения изображены
неверно.
Задачи для самостоятельного решения
Указать какой-нибудь отрезок, на котором существует решение уравнения с заданным начальным условием: а)

 б)
б)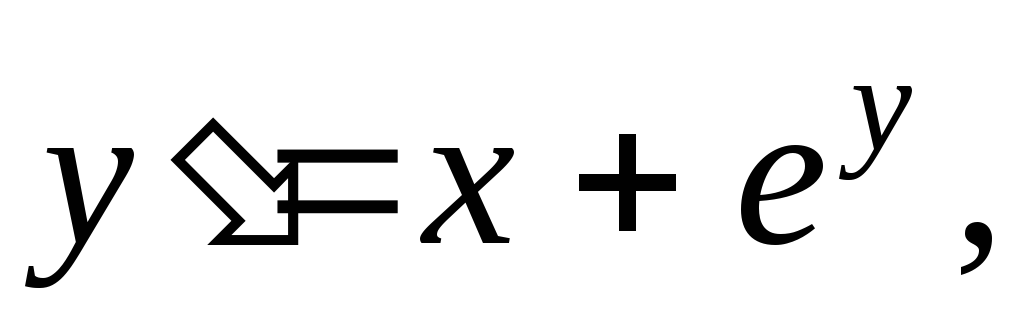

Существует ли функция
 определённая на отрезке
определённая на отрезке и удовлетворяющая уравнению
и удовлетворяющая уравнению и начальному условию
и начальному условию
Построить последовательные приближения
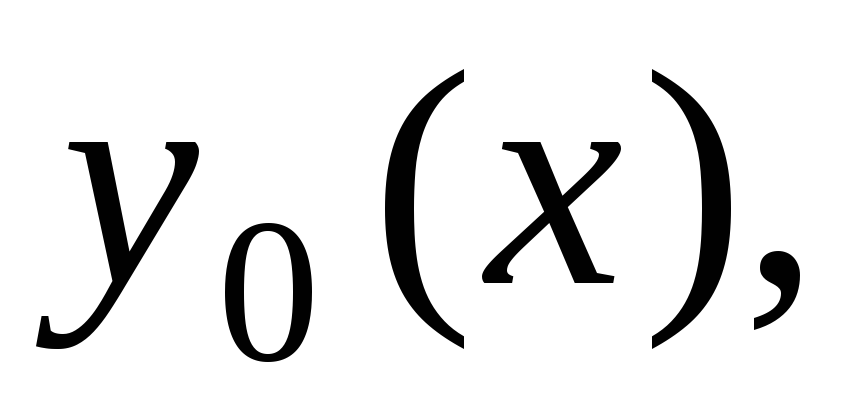
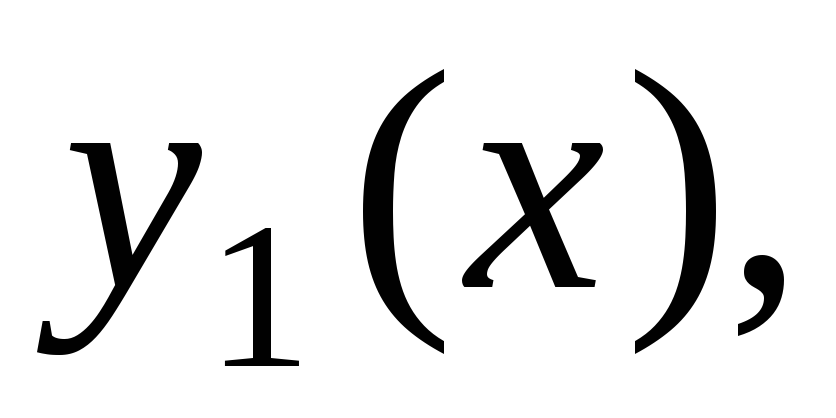
 к решению данного уравнения с данным
начальным условием: а)
к решению данного уравнения с данным
начальным условием: а)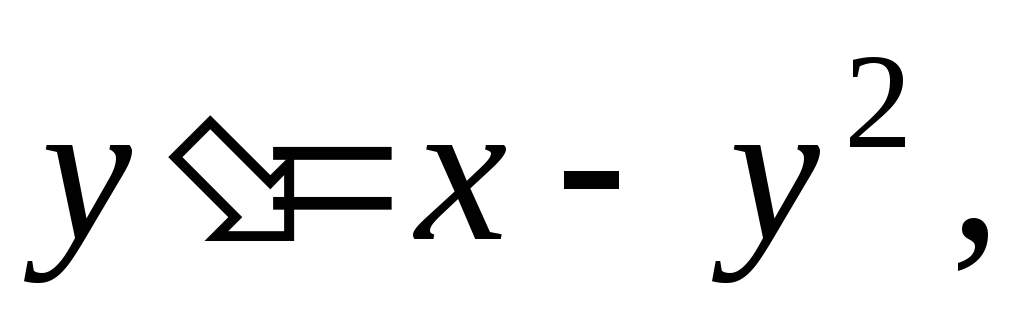
 б)
б)

Уравнение
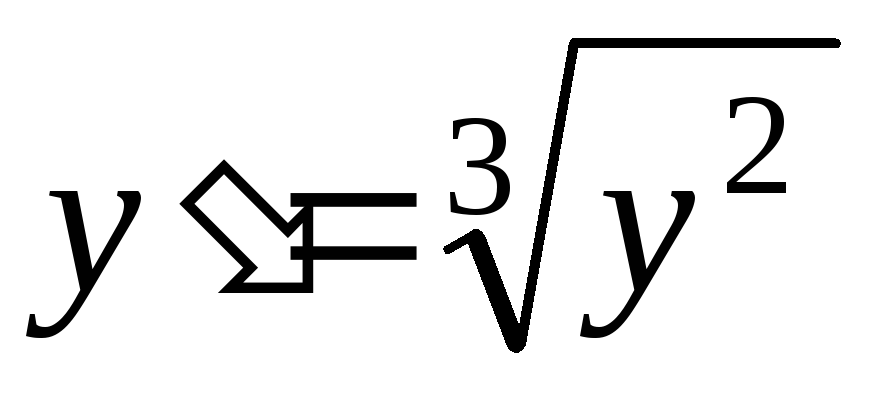 имеет два различных решения, удовлетворяющих
начальному условию
имеет два различных решения, удовлетворяющих
начальному условию это
это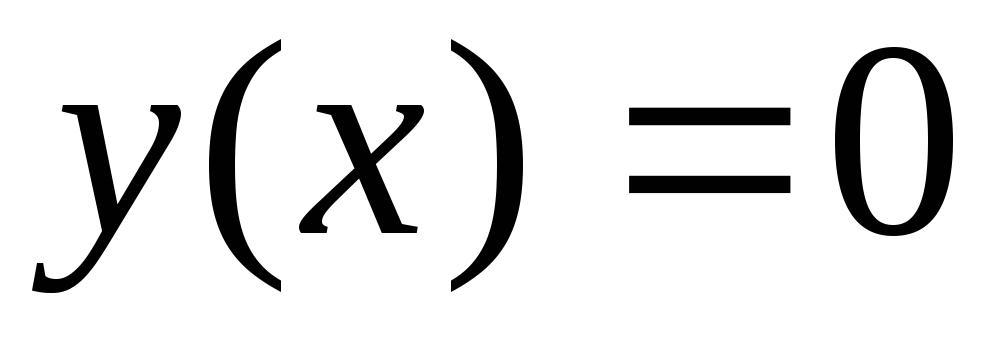 и
и Не противоречит ли данный пример теореме
существования и единственности решения?
Не противоречит ли данный пример теореме
существования и единственности решения?
Ответы:
1. а)
![]() б)
б)![]() 2. Нет. 3. а)
2. Нет. 3. а)![]()
![]()
![]() б)
б)![]()
![]()
![]() 4. Не противоречит, так как функция
4. Не противоречит, так как функция![]() не удовлетворяет условию Липшица на
отрезке
не удовлетворяет условию Липшица на
отрезке![]() где
где![]()
5. Теорема существования и единственности для дифференциальных уравнений высших порядков и систем
Пусть дана система п дифференциальных уравнений первого порядка
 (24)
(24)
Введём
в рассмотрение вектор-функции
![]() и
и![]() Тогда система (24) запишется в виде
Тогда система (24) запишется в виде
![]() (25)
(25)
Напомним,
что задача Коши для системы (25) состоит
в том, что требуется найти решение этой
системы, удовлетворяющее начальному
условию
![]() где
где![]() постоянный
вектор. Строку
постоянный
вектор. Строку![]() мы будем рассматривать как точку
пространства
мы будем рассматривать как точку
пространства![]() .
Пусть
.
Пусть![]() область в пространстве
область в пространстве![]() .
Мы будем говорить, что вектор-функция
.
Мы будем говорить, что вектор-функция![]() удовлетворяет условию Липшица по
удовлетворяет условию Липшица по![]() в области
в области![]() если существует постоянная
если существует постоянная![]() (константа
Липшица)
такая, что для любых точек
(константа
Липшица)
такая, что для любых точек
![]()
![]() имеющих одинаковую первую координату,
имеет место неравенство
имеющих одинаковую первую координату,
имеет место неравенство
![]() (26)
(26)
Здесь
модули обозначают длины векторов в
пространстве
![]() .
Для системы (25), как и для уравнения
(20), справедлива теорема существования
и единственности решения.
.
Для системы (25), как и для уравнения
(20), справедлива теорема существования
и единственности решения.
Теорема
существования и единственности решения
системы.
Пусть
![]() область в пространстве
область в пространстве![]() ,
,![]() вектор-функция,
определённая в области
вектор-функция,
определённая в области![]() причём
причём![]() в этой области непрерывна по
в этой области непрерывна по![]() и удовлетворяет условию Липшица по
и удовлетворяет условию Липшица по![]() Тогда для каждой точки
Тогда для каждой точки![]() области
области![]() существует окрестность
существует окрестность![]()
![]() в которой система дифференциальных
уравнений
в которой система дифференциальных
уравнений![]() имеет единственное решение, удовлетворяющее
начальному условию
имеет единственное решение, удовлетворяющее
начальному условию![]()
Доказательство этой теоремы проводится совершенно аналогично доказательству теоремы существования и единственности решения уравнения первого порядка.
Дифференциальное уравнение п-го порядка, разрешённое относительно старшей производной, имеет вид
![]() (25)
(25)
Задача Коши для этого уравнения ставится следующим образом: требуется найти решение уравнения (25), удовлетворяющего начальному условию
![]()
![]() .
. .
.
. .
![]() (26)
(26)
где
![]() заданные действительные числа. Здесь
заданные действительные числа. Здесь![]() не означает дифференцирования. Очевидно,
уравнение (25)п-го
порядка равносильно системе уравнений
первого порядка, а именно, системе
не означает дифференцирования. Очевидно,
уравнение (25)п-го
порядка равносильно системе уравнений
первого порядка, а именно, системе
 (27)
(27)
Начальное
условие для системы (27) получается из
(26) и имеет вид
![]() Теорема существования и единственности
решения уравнения (25) является
непосредственным следствием теоремы
существования и единственности решения
системы. Приведём формулировку теоремы.
Теорема существования и единственности
решения уравнения (25) является
непосредственным следствием теоремы
существования и единственности решения
системы. Приведём формулировку теоремы.
Теорема
существования и единственности решения
уравнения п-го
порядка.
Пусть
![]() функция, которая в некоторой области
функция, которая в некоторой области![]() пространства
пространства![]() непрерывна пох
и удовлетворяет условию Липшица по
непрерывна пох
и удовлетворяет условию Липшица по
![]() Тогда для каждой точки
Тогда для каждой точки![]() существует окрестность, в которой
решение уравнения
существует окрестность, в которой
решение уравнения![]() удовлетворяющее начальному условию
удовлетворяющее начальному условию![]()
![]() . . .
. . .![]() существует и единственно.
существует и единственно.
Для
систем дифференциальных уравнений
первого порядка, как и для одного
уравнения первого порядка, решение
может быть найдено методом последовательных
приближений. А именно, если рассматривается
уравнение
![]() с начальным условием
с начальным условием![]() то для достаточно малого
то для достаточно малого![]() последовательность вектор-функций
последовательность вектор-функций![]()
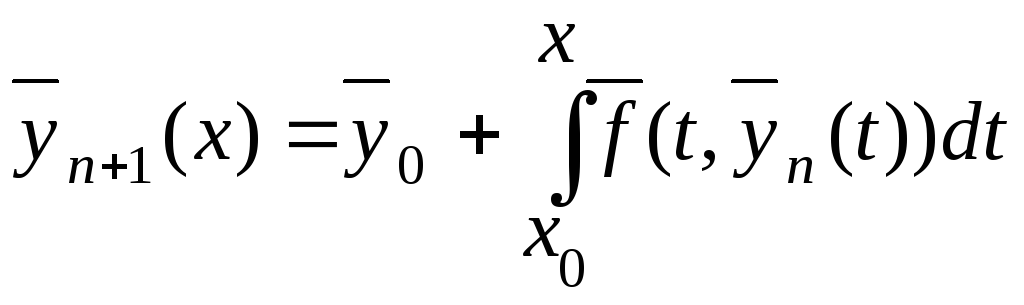
![]() равномерно сходится к решению
равномерно сходится к решению![]() если вектор-функция
если вектор-функция![]() непрерывна пох
и удовлетворяет условию Липшица по
непрерывна пох
и удовлетворяет условию Липшица по
![]()
