
- •Глава 3. Существование и единственность решения дифференциального уравнения
- •1. Метрические пространства
- •Типовые задачи
- •Задачи для самостоятельного решения
- •Полные пространства
- •Типовые задачи
- •Задачи для самостоятельного решения
- •3. Принцип сжимающих отображений
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6. Теорема существования и единственности для линейных уравнений и систем
Типовые задачи
Доказать эквивалентность на R
 метрик
метрик определяемых формулами (5), (6), (7).
определяемых формулами (5), (6), (7).
Доказательство.
Пусть![]() R
R![]() и
и![]()
![]()
![]() Тогда
Тогда![]() при всех
при всех![]() Следовательно,
Следовательно,![]() Далее,
Далее,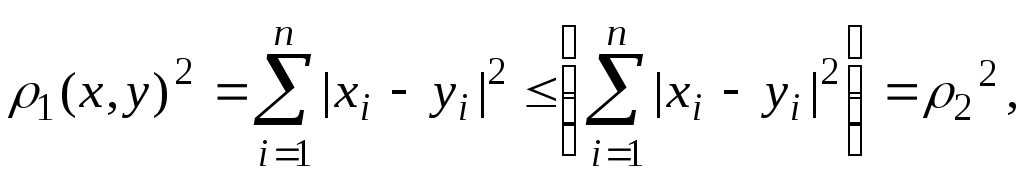 т.е.
т.е.![]() Наконец, ясно, что
Наконец, ясно, что![]() Таким образом,
Таким образом,![]() значит, метрики
значит, метрики![]() эквивалентны.
эквивалентны.
Какие последовательности сходятся в дискретном пространстве?
Решение.
Пусть![]() дискретное пространство,
дискретное пространство,![]() последовательность
точек изХи
последовательность
точек изХи![]() Тогда
Тогда![]() при
при![]() Взяв
Взяв![]() получим:
получим:![]() при
при![]() Таким образом, сходящимися являются те
и только те последовательности
Таким образом, сходящимися являются те
и только те последовательности![]() которыестабилизируются, т.е. обладают
свойством
которыестабилизируются, т.е. обладают
свойством![]() при некотором
при некотором![]()
Выяснить, является ли дискретное пространство полным.
Решение.
Пусть![]() фундаментальная последовательность в
дискретном пространствеХ. Тогда
фундаментальная последовательность в
дискретном пространствеХ. Тогда![]() при
при![]() Взяв
Взяв![]() получим, что
получим, что![]() при
при![]() Отсюда видно, что
Отсюда видно, что![]() сходящаяся последовательность. Значит,Хполно.
сходящаяся последовательность. Значит,Хполно.
Выяснить, сходятся ли в
 последовательности: а)
последовательности: а) б)
б) в)
в)
Решение.
а) Если![]() сходится в
сходится в![]() к функции
к функции![]() то
то![]() при
при![]() и всех
и всех![]() Подставив любое
Подставив любое![]() мы получим
мы получим![]() а подставив
а подставив![]() получим
получим![]() Таким образом, функция
Таким образом, функция![]() не является непрерывной на отрезке
не является непрерывной на отрезке![]() а значит,
а значит,![]() расходится.
расходится.
б) При
каждом фиксированном
![]() мы имеем:
мы имеем:![]() Значит, если
Значит, если![]() сходится в
сходится в![]() то сходится к функции, тождественно
равной нулю, и
то сходится к функции, тождественно
равной нулю, и![]() Найдём наибольшее значение функции
Найдём наибольшее значение функции![]() на отрезке
на отрезке![]() Имеем:
Имеем:![]() откуда
откуда![]() или
или![]() Далее,
Далее,![]() Так как
Так как![]() то
то![]() при
при![]() Следовательно,
Следовательно,![]()
в) При
каждом фиксированном
![]() мы имеем:
мы имеем:![]() Далее,
Далее,![]() Следовательно,
Следовательно,![]() при
при![]() и
и![]() .
Так как
.
Так как![]() не стремится к нулю, то
не стремится к нулю, то![]() не сходится в
не сходится в![]()
Выяснить, является ли полным пространство Рмногочленов с нормой

Решение.
Пространство многочленов рассматривается
здесь как подпространство пространства![]() Известно, что
Известно, что![]() Рассмотрим последовательность многочленов
Рассмотрим последовательность многочленов![]() .
Ясно, что
.
Ясно, что![]() т.е. последовательность
т.е. последовательность![]() сходится к функции
сходится к функции![]() в пространстве
в пространстве![]() Так как функция
Так как функция![]() не является многочленом, то
не является многочленом, то![]() фундаментальная последовательность в
пространстве
фундаментальная последовательность в
пространстве![]() не являющаяся сходящейся. Следовательно,
не являющаяся сходящейся. Следовательно,![]() не полно.
не полно.
Привести пример последовательности, которая сходится в пространстве
 но не сходится в
но не сходится в
Решение.
Примером может служить последовательность![]() Так как
Так как то
то![]() не сходится в
не сходится в![]() Однако, она сходится в
Однако, она сходится в![]() к нулю, так как
к нулю, так как![]() при
при![]()
Задачи для самостоятельного решения
Эквивалентны ли метрики
 и
и на
на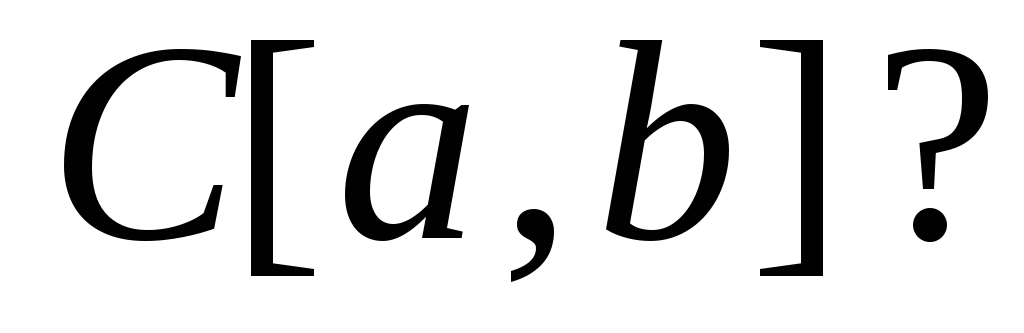
Является ли полным пространство
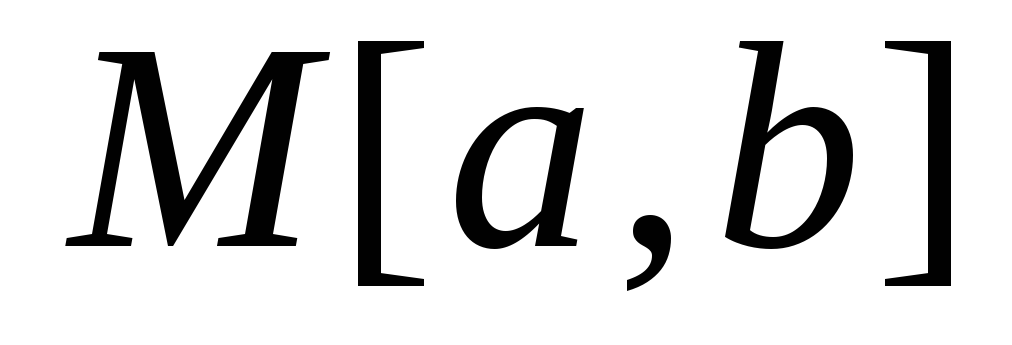 всех функций, ограниченных на отрезке
всех функций, ограниченных на отрезке с нормой
с нормой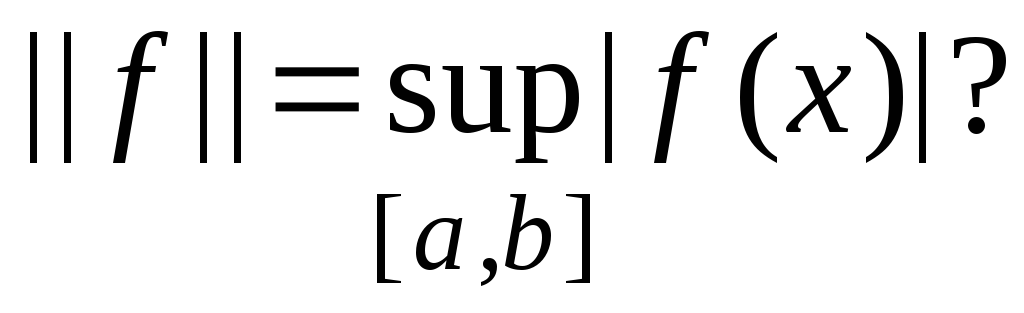
Пусть
 и
и последовательности точек нормированного
пространстваХ, причём
последовательности точек нормированного
пространстваХ, причём сходится, а
сходится, а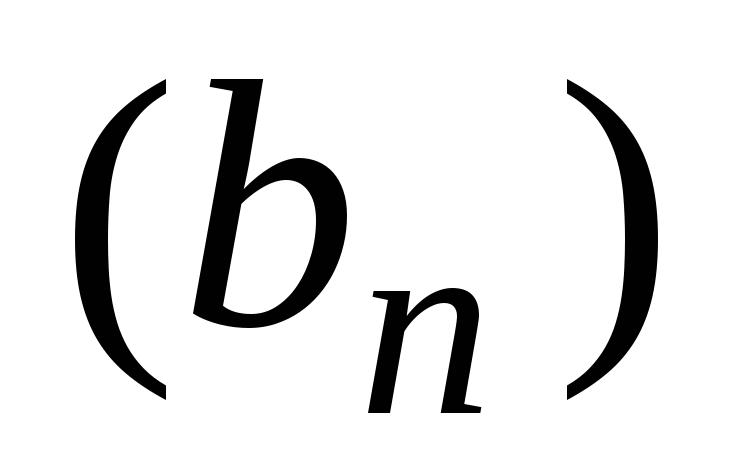 расходится. Сходится ли последовательность
расходится. Сходится ли последовательность
Привести пример фундаментальной, но не сходящейся последовательности в пространстве R с метрикой

Пусть
 пространство всех функций, имеющих
непрерывную производную на отрезке
пространство всех функций, имеющих
непрерывную производную на отрезке с нормой
с нормой Какое из утверждений истинно для
последовательностей
Какое из утверждений истинно для
последовательностей
(А) если
![]() сходится в
сходится в![]() то
то![]() сходится в
сходится в![]()
(Б) если
![]() сходится в
сходится в![]() то
то![]() сходится в
сходится в![]()
Ответы:1. Нет. 2. Да. 3. Расходится. 4.![]() 5. (А) ложно, (Б) истинно.
5. (А) ложно, (Б) истинно.
3. Принцип сжимающих отображений
Пусть
![]() метрическое пространство. Отображение
метрическое пространство. Отображение![]() называетсясжимающим,
если существует такое
называетсясжимающим,
если существует такое
![]() что
что![]() и
и![]() при всех
при всех![]()
Пусть
![]() метрическое пространство и
метрическое пространство и![]() отображение. Говорят, что точка
отображение. Говорят, что точка![]() являетсянеподвижной
точкой
отображения Т,
если
являетсянеподвижной
точкой
отображения Т,
если
![]()
Теорема
(принцип
сжимающих отображений).
Если
![]() сжимающее отображение полного метрического
пространстваХ,
то Т
имеет единственную неподвижную точку.
сжимающее отображение полного метрического
пространстваХ,
то Т
имеет единственную неподвижную точку.
Доказательство.
Возьмём любую точку
![]() и образуем последовательность
и образуем последовательность![]()
![]()
![]() Докажем, что эта последовательность
сходится, и её предел является единственной
неподвижной точкой отображения
Докажем, что эта последовательность
сходится, и её предел является единственной
неподвижной точкой отображения![]() Доказательство разобьём на несколько
шагов.
Доказательство разобьём на несколько
шагов.
Оценим сверху расстояние между соседними членами последовательности. Имеем:
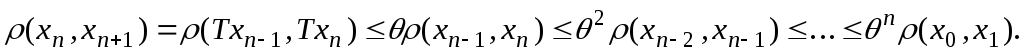
Докажем, что последовательность
 фундаментальна. Для этого оценим
расстояние между произвольными членами
последовательности. Имеем:
фундаментальна. Для этого оценим
расстояние между произвольными членами
последовательности. Имеем: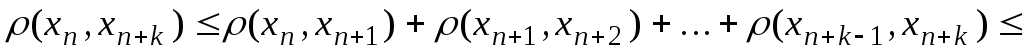
![]()
![]() Так
как
Так
как
![]() то
то![]() при
при![]() поэтому
поэтому![]() при
при![]() и
и![]() Это означает, что последовательность
Это означает, что последовательность![]() фундаментальна.
фундаментальна.
Так как
 фундаментальна иХ
полно, то
фундаментальна иХ
полно, то
 сходится. Пусть
сходится. Пусть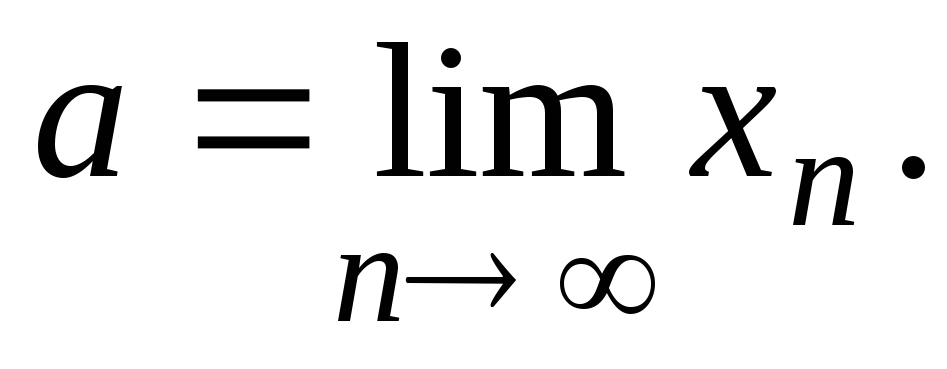 Докажем, что
Докажем, что неподвижная точка отображенияТ.
Имеем:
неподвижная точка отображенияТ.
Имеем:

 при
при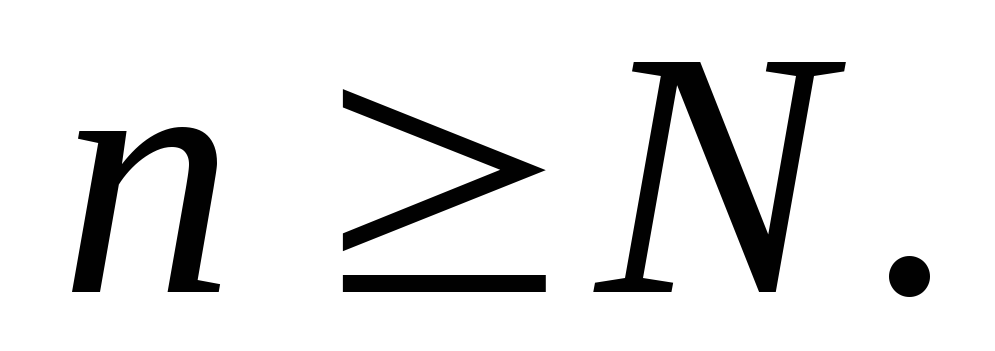 Ввиду произвольности числа
Ввиду произвольности числа мы получаем, что
мы получаем, что Из аксиом метрики следует, что
Из аксиом метрики следует, что следовательно,
следовательно, неподвижная точка.
неподвижная точка.Докажем, что других неподвижных точек у отображения Т нет. Действительно, пусть
 Тогда
Тогда Так как
Так как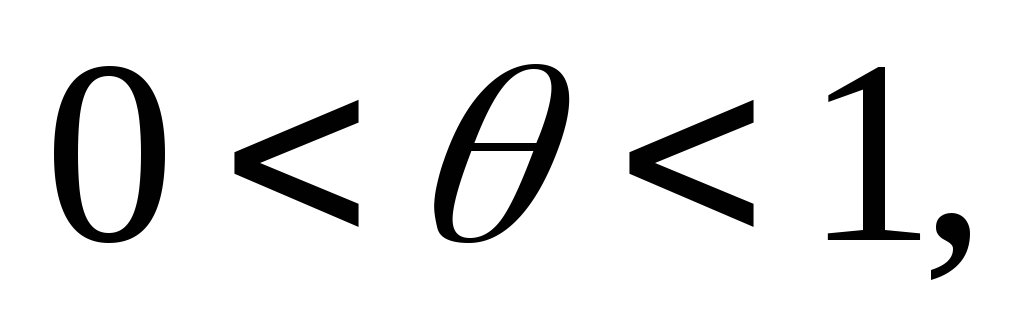 то
то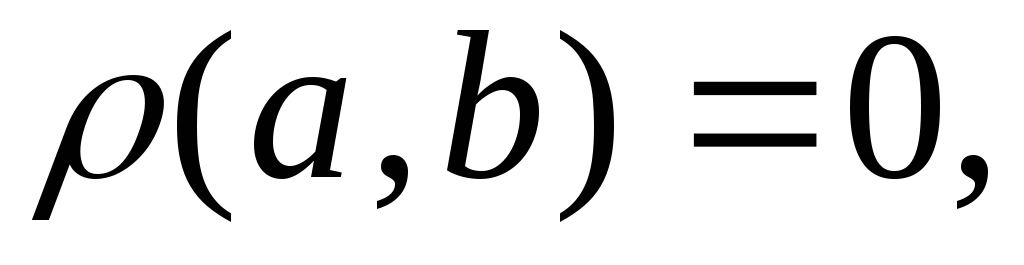 а значит,
а значит,
4. Теорема существования и единственности решения дифференциального уравнения первого порядка
![]() Напомним,
что областью
в пространстве R
Напомним,
что областью
в пространстве R![]() называетсясвязное
открытое множество.
Связность означает, что любые две точки
множества можно соединить непрерывной
кривой, не выходящей за пределы множества.
Множество открытое, если любая его точка
внутренняя,
т.е. имеет окрестность, лежащую внутри
области.
называетсясвязное
открытое множество.
Связность означает, что любые две точки
множества можно соединить непрерывной
кривой, не выходящей за пределы множества.
Множество открытое, если любая его точка
внутренняя,
т.е. имеет окрестность, лежащую внутри
области.
Пусть
дано дифференциальное уравнение
![]() где функция
где функция![]() определена в некоторой области
определена в некоторой области![]() плоскостиR
плоскостиR![]() Естественным требованием на функцию
Естественным требованием на функцию![]() является её непрерывность в области
является её непрерывность в области![]() Однако, этого для существования и
единственности решения оказывается
недостаточным. Введём ещё одно условие.
А именно, будем говорить, что функция
Однако, этого для существования и
единственности решения оказывается
недостаточным. Введём ещё одно условие.
А именно, будем говорить, что функция![]() удовлетворяетусловию
Липшица
по переменной у
в области
удовлетворяетусловию
Липшица
по переменной у
в области
![]() ,
если существует постоянная
,
если существует постоянная![]() (константа
Липшица)
такая, что
(константа
Липшица)
такая, что
![]() (17)
(17)
для
всех
![]() Условие Липшица сильнее, чем непрерывность
по переменнойу,
но слабее, чем дифференцируемость.
Точнее, справедливы утверждения:
Условие Липшица сильнее, чем непрерывность
по переменнойу,
но слабее, чем дифференцируемость.
Точнее, справедливы утверждения:
(![]() если функция
если функция![]() удовлетворяет условию Липшица поу,
то она непрерывна по у;
удовлетворяет условию Липшица поу,
то она непрерывна по у;
(![]() если
если![]() имеет в области
имеет в области![]() ограниченную производную поу,
то она удовлетворяет условию Липшица
по у.
ограниченную производную поу,
то она удовлетворяет условию Липшица
по у.
Докажем
утверждения (![]() ),
(
),
(![]() Действительно, из условия (17) следует,
что
Действительно, из условия (17) следует,
что![]() а это означает непрерывность функции
а это означает непрерывность функции![]() по переменной
по переменной![]() т.е. выполнено (
т.е. выполнено (![]() Далее, пусть
Далее, пусть![]() для всех точек области
для всех точек области![]() Тогда по теореме Лагранжа для некоторого
Тогда по теореме Лагранжа для некоторого![]() мы имеем:
мы имеем:![]() что доказывает
что доказывает![]() В качестве константы Липшица здесь
можно взять константуК.
В качестве константы Липшица здесь
можно взять константуК.
Во многих вопросах теории дифференциальных уравнений и, в частности, для доказательства теоремы существования и единственности удобно заменить дифференциальное уравнение интегральным. Возможность такой замены вытекает из следующего утверждения.
Лемма.
Если
![]() непрерывная функция, то система уравнений
непрерывная функция, то система уравнений
![]() (18)
(18)
состоящая из дифференциального уравнения и начального условия, равносильна интегральному уравнению
 (19)
(19)
Доказательство.
Пусть функция
![]() определённая на интервале
определённая на интервале![]() удовлетворяет системе (18). Проинтегрировав
равенство
удовлетворяет системе (18). Проинтегрировав
равенство![]() получим:
получим: Так как
Так как![]() то
то![]() Следовательно, выполнено (19).
Следовательно, выполнено (19).
Наоборот,
пусть функция
![]() удовлетворяет интегральному уравнению
(19). Тогда
удовлетворяет интегральному уравнению
(19). Тогда значит, выполнено начальное условие.
Продифференцировав равенство (19) по
значит, выполнено начальное условие.
Продифференцировав равенство (19) по![]() получим:
получим:![]() поэтому функция
поэтому функция![]() удовлетворяет дифференциальному
уравнению.
удовлетворяет дифференциальному
уравнению.
Теорема существования и единственности решения уравнения первого порядка. Пусть дано дифференциальное уравнение
![]() (20)
(20)
причём
функция
![]() в некоторой области
в некоторой области![]() плоскостиR
плоскостиR![]() непрерывна пох
и удовлетворяет условию Липшица по у.
Тогда для каждой точки
непрерывна пох
и удовлетворяет условию Липшица по у.
Тогда для каждой точки
![]() области
области![]() существует такое
существует такое![]() что на отрезке
что на отрезке![]() существует единственная функция
существует единственная функция![]() удовлетворяющая дифференциальному
уравнению (20) и начальному условию
удовлетворяющая дифференциальному
уравнению (20) и начальному условию![]()
Доказательство.
Во-первых, заменим дифференциальное
уравнение с начальным условием на
интегральное уравнение (19). Затем выберем
числа
![]() так, чтобы прямоугольник
так, чтобы прямоугольник![]() лежал в области
лежал в области![]() Обозначим через
Обозначим через![]() множество функций, непрерывных на
отрезке
множество функций, непрерывных на
отрезке![]() и удовлетворяющих условиям
и удовлетворяющих условиям
![]() (21)
(21)
Очевидно,
![]() является подпространством пространства
является подпространством пространства![]() Пространство
Пространство![]() полно – его полнота доказывается так
же, как полнота пространства
полно – его полнота доказывается так
же, как полнота пространства![]() Обозначим через
Обозначим через![]() оператор на множестве функций, переводящий
функциюу
в функцию
оператор на множестве функций, переводящий
функциюу
в функцию
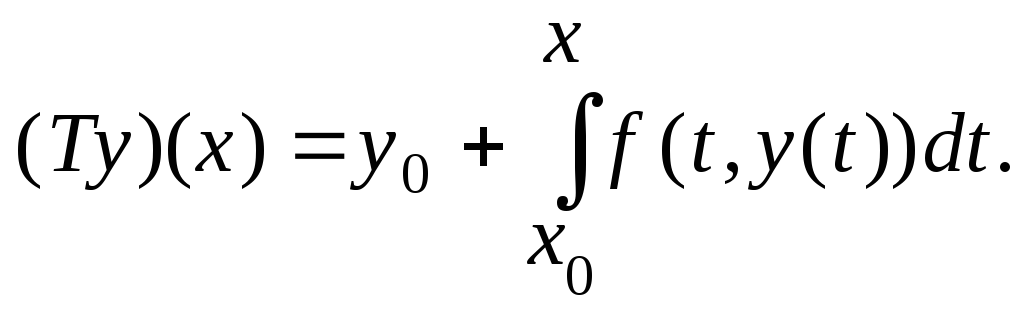 (22)
(22)
Проверим,
что при достаточно малом
![]() операторТ
будет являться отображением из
операторТ
будет являться отображением из
![]() в
в![]() причём сжимающим. Действительно, из
условия теоремы следует, что функция
причём сжимающим. Действительно, из
условия теоремы следует, что функция![]() непрерывна в прямоугольнике
непрерывна в прямоугольнике![]() поэтому существует постоянная
поэтому существует постоянная![]() такая, что
такая, что![]() при
при![]() Пусть
Пусть![]() и
и![]() Тогда
Тогда![]() Следовательно,
Следовательно, Если теперь
Если теперь![]() то
то![]() при
при![]() а значит,
а значит,![]()
 Докажем
теперь сжимаемость оператора Т.
Пусть
Докажем
теперь сжимаемость оператора Т.
Пусть
![]() и
и![]() Мы имеем:
Мы имеем: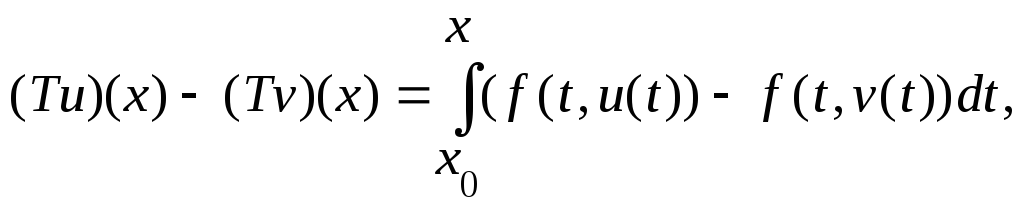 поэтому
поэтому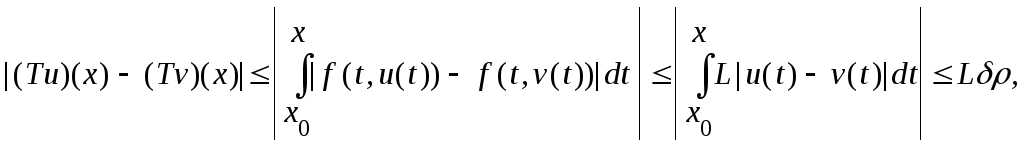 следовательно,
следовательно,![]() Так как
Так как![]() то
то![]() поэтому
поэтому![]() сжимающий оператор. По принципу сжимающих
отображений существует единственная
функция
сжимающий оператор. По принципу сжимающих
отображений существует единственная
функция![]() такая, что
такая, что![]() Это означает, что уравнение (20) имеет
единственное решение, удовлетворяющее
начальному условию
Это означает, что уравнение (20) имеет
единственное решение, удовлетворяющее
начальному условию![]() Предположение о том, что
Предположение о том, что![]() не сужает класса рассматриваемых
функций, так как для всякой непрерывной
на отрезке функции это неравенство
выполняется при подходящем
не сужает класса рассматриваемых
функций, так как для всякой непрерывной
на отрезке функции это неравенство
выполняется при подходящем![]()
Теорему
существования и единственности можно
переформулировать так: для “достаточно
хорошей” функции
![]() (а именно, если
(а именно, если![]() непрерывна пох
и удовлетворяет условию Липшица по у
в области
непрерывна пох
и удовлетворяет условию Липшица по у
в области
![]() ),
то через каждую точку области
),
то через каждую точку области![]() проходит единственная интегральная
кривая уравнения
проходит единственная интегральная
кривая уравнения![]() Таким образом, эта теорема носитлокальный
характер,
т.е. для каждой точки утверждается лишь
существование окрестности, в которой
решение существует и единственно.
Решение, найденное на промежутке
Таким образом, эта теорема носитлокальный
характер,
т.е. для каждой точки утверждается лишь
существование окрестности, в которой
решение существует и единственно.
Решение, найденное на промежутке
![]() далеко не всегда может быть продолжено
на промежуток
далеко не всегда может быть продолжено
на промежуток![]() даже если существует прямоугольник
даже если существует прямоугольник![]() лежащий в области
лежащий в области![]() Однако, применяя теорему существования
и единственности несколько раз (переходя
от точки
Однако, применяя теорему существования
и единственности несколько раз (переходя
от точки![]() к точке
к точке![]() ,
затем к
,
затем к![]() и т.д., можно убедиться в том, что всякое
решение продолжается либо до границы
области
и т.д., можно убедиться в том, что всякое
решение продолжается либо до границы
области![]() (возможно, не достигая этой границы),
либо “уходит в бесконечность” (это
может быть лишь в случае, когда область
(возможно, не достигая этой границы),
либо “уходит в бесконечность” (это
может быть лишь в случае, когда область![]() неограниченна).
неограниченна).
Доказательство
теоремы существования и единственности
даёт также метод решения дифференциальных
уравнений, который можно использовать
на практике для приближённого их решения.
Это метод
последовательных приближений.
Суть этого метода заключается в следующем.
Пусть требуется найти решение
дифференциального уравнения
![]() удовлетворяющего начальному условию
удовлетворяющего начальному условию![]() Рассмотрим последовательность функций,
определённых на отрезке
Рассмотрим последовательность функций,
определённых на отрезке![]()
![]()

 и
т.д., т.е. для любого
и
т.д., т.е. для любого
![]() полагаем
полагаем Тогда для достаточно малого
Тогда для достаточно малого![]() мы имеем:
мы имеем:![]() при
при![]() где
где![]() решение дифференциального уравнения.
Начальное условие
решение дифференциального уравнения.
Начальное условие![]() для функций
для функций![]() а значит, и для функции
а значит, и для функции![]() очевидно, также выполнено.
очевидно, также выполнено.
