
- •Глава 3. Существование и единственность решения дифференциального уравнения
- •1. Метрические пространства
- •Типовые задачи
- •Задачи для самостоятельного решения
- •Полные пространства
- •Типовые задачи
- •Задачи для самостоятельного решения
- •3. Принцип сжимающих отображений
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •6. Теорема существования и единственности для линейных уравнений и систем
Типовые задачи
Выяснить, является ли метрическим пространством данное множество:
а)
множество всех ограниченных
последовательностей
![]() действительных чисел, где расстояние
между
действительных чисел, где расстояние
между![]() и
и![]() определяется формулой
определяется формулой![]()
б)
множество всех интервалов
![]() числовой прямой, где
числовой прямой, где![]()
в)
множество R
всех действительных чисел, где
![]()
г)
множество всех многочленов
![]() где
где![]() R,
а расстояние между
R,
а расстояние между
![]() и
и![]() определяется по формуле
определяется по формуле![]()
Решение.
а) Данное множество является метрическим
пространством, даже нормированным,
причём норма выражается формулой
![]() Проверим это. Выполнение аксиом (Н1),
(Н2) здесь очевидно. Кроме того,
Проверим это. Выполнение аксиом (Н1),
(Н2) здесь очевидно. Кроме того,![]() значит, выполнена аксиома (Н3).
значит, выполнена аксиома (Н3).
б)
Данное множество не является метрическим
пространством, так как не выполнена
аксиома (М1). Действительно, для элементов
![]() и
и![]() например, мы имеем:
например, мы имеем:![]() но
но![]()
в)
Проверим, что (R,![]() метрическое пространство. Здесь
выполнение аксиом (М1), (М2) очевидно,
нужно проверить лишь неравенство
треугольника. Имеем:
метрическое пространство. Здесь
выполнение аксиом (М1), (М2) очевидно,
нужно проверить лишь неравенство
треугольника. Имеем:![]() значит, аксиома (М3) также выполнена.
значит, аксиома (М3) также выполнена.
г)
Положим
![]() Ясно, что
Ясно, что![]() и
и![]() Далее, при
Далее, при![]() R
имеем:
R
имеем:
![]() т.е. выполнено (Н2). Наконец,
т.е. выполнено (Н2). Наконец,![]() т.е. выполнено (Н3). Таким образом, множество
многочленов является нормированным, а
значит, и метрическим пространством.
т.е. выполнено (Н3). Таким образом, множество
многочленов является нормированным, а
значит, и метрическим пространством.
2.
Доказать, что евклидово пространство
![]() над полем действительных чисел (т.е.
пространство со скалярным произведением)
будет являться нормированным пространством,
если положить
над полем действительных чисел (т.е.
пространство со скалярным произведением)
будет являться нормированным пространством,
если положить![]() для всех
для всех![]()
![]()
Доказательство.
Из аксиом скалярного произведения
следует, что
![]() и
и![]() Кроме того,
Кроме того,![]() Наконец, из неравенства Шварца (
Наконец, из неравенства Шварца (![]() )
получаем:
)
получаем:![]()
![]() откуда
следует неравенство треугольника.
откуда
следует неравенство треугольника.
3.
Вычислить норму функции
![]() а) в пространстве
а) в пространстве![]() б) в пространстве
б) в пространстве![]() в) ) в пространстве
в) ) в пространстве![]()
Решение.
а)
![]() б)
б)![]() в)
в)![]()
Доказать, что если
 метрика на множествеХ,
то
метрика на множествеХ,
то
 тоже метрика.
тоже метрика.
Доказательство.
Так как
![]() то
то![]() При этом
При этом![]() и
и![]() Осталось доказать неравенство
треугольника. Для краткости положим
Осталось доказать неравенство
треугольника. Для краткости положим![]()
![]()
![]()
![]()
![]() Так как
Так как![]() метрика, то
метрика, то![]() Отсюда
Отсюда![]() т.е.
т.е.![]()
Вычислить расстояние между функциями
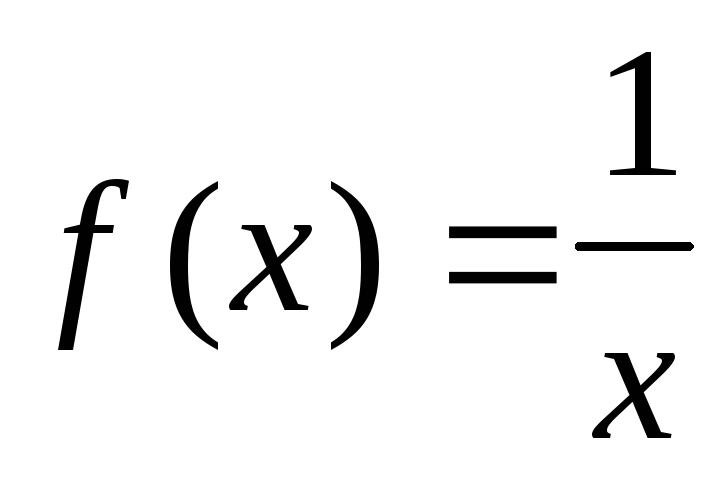 и
и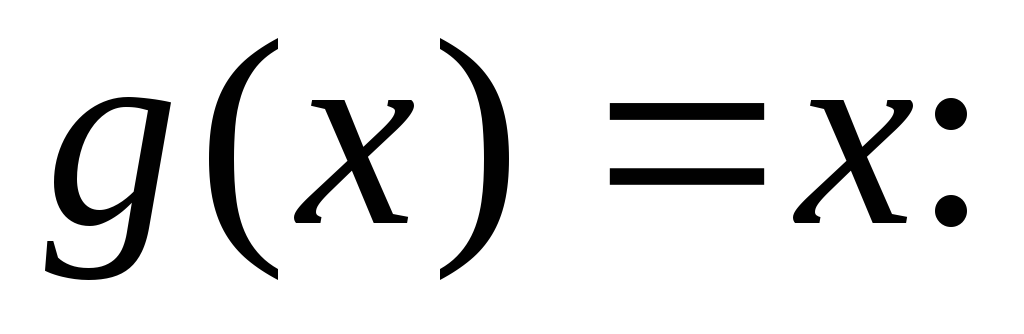 а) в пространстве
а) в пространстве б) в пространстве
б) в пространстве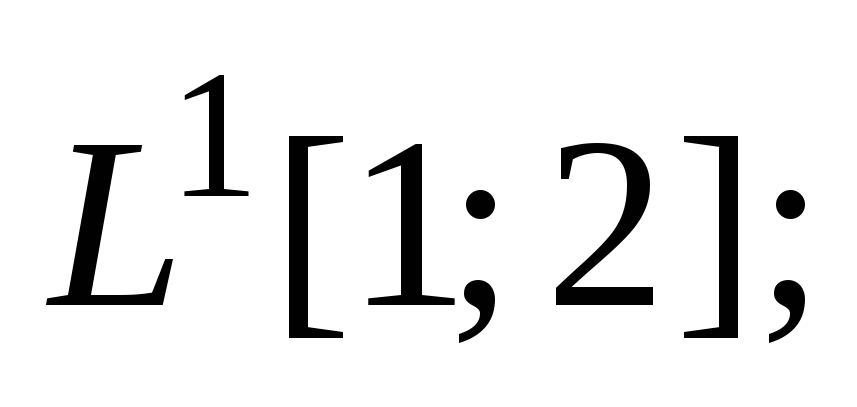 в) в пространстве
в) в пространстве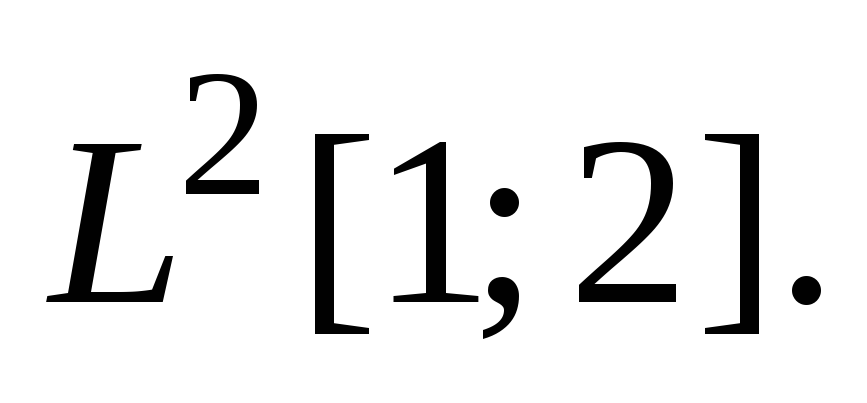
Решение.
а)
![]()
б)
![]()
в)
![]()
Задачи для самостоятельного решения
Доказать, что если
 метрика
пространстваХ,
то
метрика
пространстваХ,
то
 и
и также метрики наХ.
также метрики наХ.Является ли метрикой на множестве R следующая функция:
а)
![]() б)
б)![]() в)
в)![]()
Вычислить норму функции
 а) в пространстве
а) в пространстве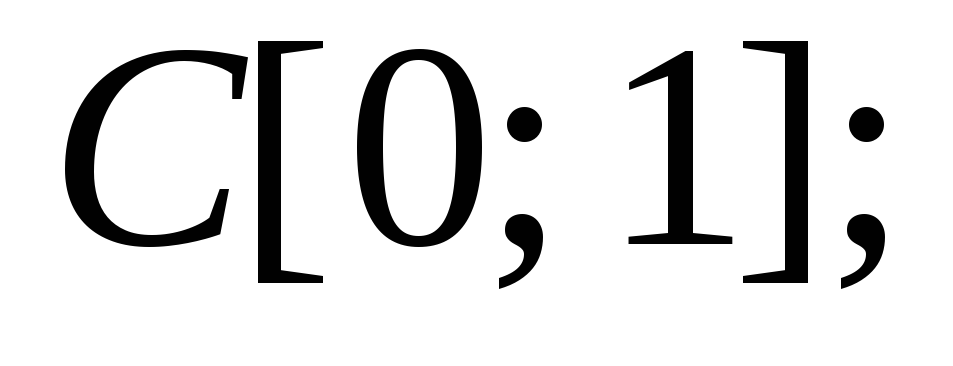 б) в пространстве
б) в пространстве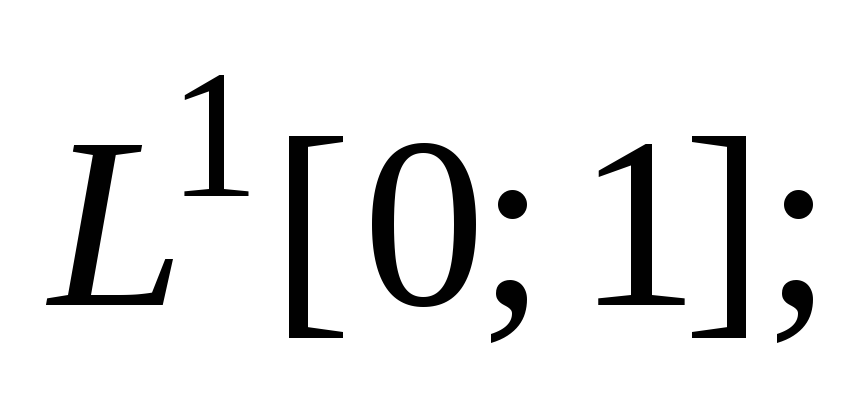 в) в пространстве
в) в пространстве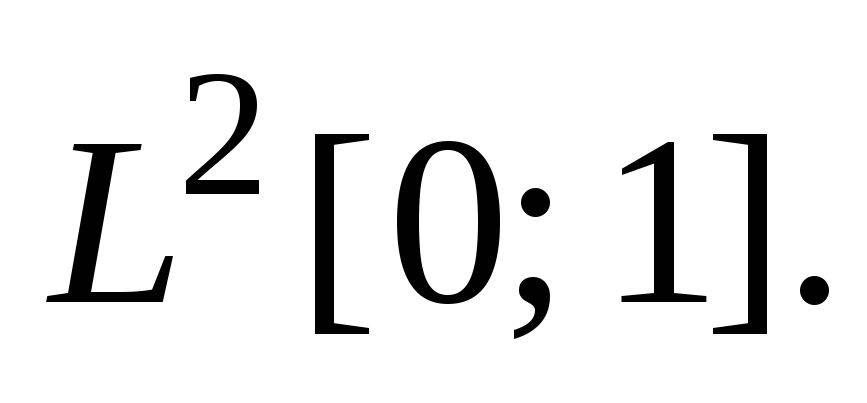
Вычислить расстояние между функциями
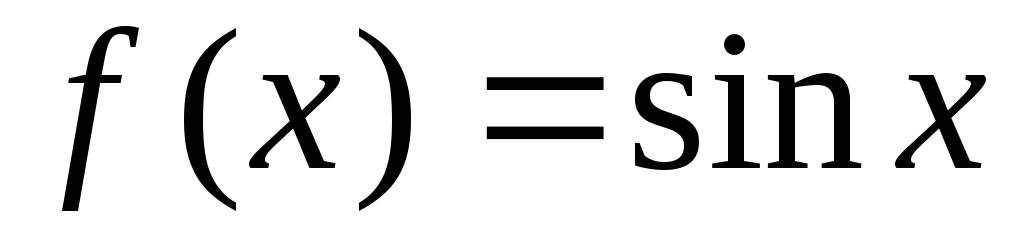 и
и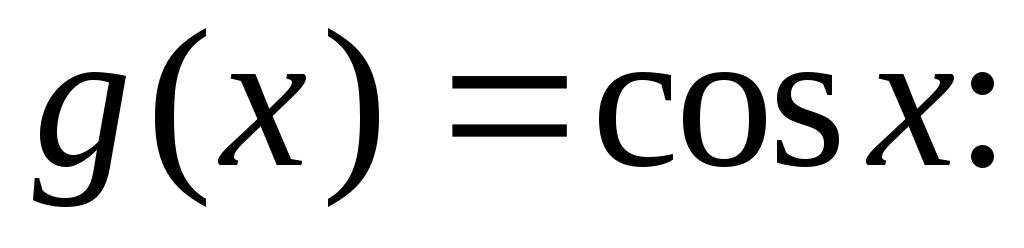 а) в пространстве
а) в пространстве б) в пространстве
б) в пространстве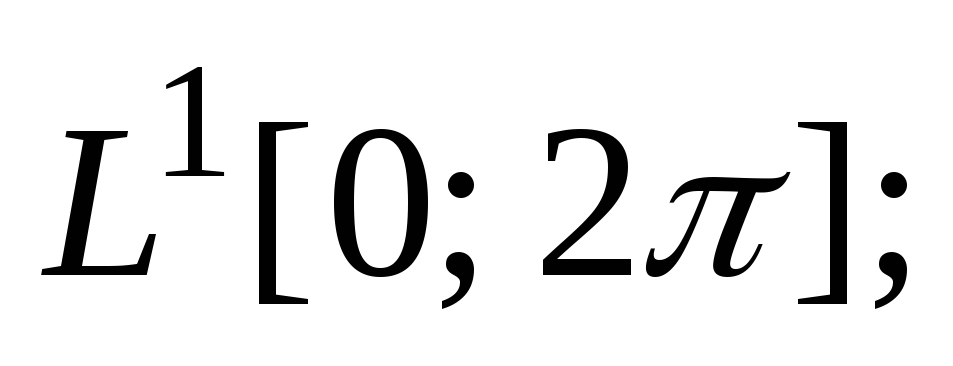 в) в пространстве
в) в пространстве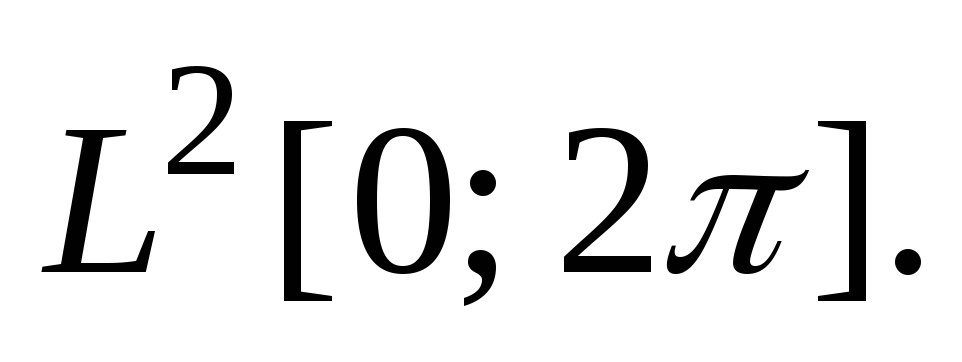
Доказать, что если в нормированном пространстве Х норма определяется скалярным произведением, то имеет место равенство
![]() (равенство
параллелограмма).
Вывести отсюда, что в пространстве
(равенство
параллелограмма).
Вывести отсюда, что в пространстве
![]() норма не определяется скалярным
произведением.
норма не определяется скалярным
произведением.
Ответы:
2. а) нет; б)
да; в) нет. 3. а)
![]() б)
б)![]() в)
в)![]() 4. а)
4. а)![]() б)
б)![]()
![]()
2. Предел последовательности в метрическом пространстве.
Полные пространства
Пусть
![]() метрическое пространство и
метрическое пространство и![]() произвольное
подмножество множестваХ.
Тогда
произвольное
подмножество множестваХ.
Тогда
![]() будет являться метрическим пространством,
если в качестве расстояния
будет являться метрическим пространством,
если в качестве расстояния![]() между точками
между точками![]() взять расстояние между этими точками
в пространствеХ.
В этом случае говорят, что
взять расстояние между этими точками
в пространствеХ.
В этом случае говорят, что
![]() являетсяподпространством
пространства Х.
Например, пространство Q
рациональных чисел является
подпространством числовой прямой R,
если положить
являетсяподпространством
пространства Х.
Например, пространство Q
рациональных чисел является
подпространством числовой прямой R,
если положить
![]() для
для![]() Q.
Q.
Предел
последовательности
![]() точек метрического пространстваХ
определяется аналогично пределу обычной
числовой последовательности. А именно,
точек метрического пространстваХ
определяется аналогично пределу обычной
числовой последовательности. А именно,
![]() (14)
(14)
Последовательность
называется сходящейся,
если она имеет предел; в противном случае
последовательность называется
расходящейся.
Если
![]() нормированное пространство, то неравенство
нормированное пространство, то неравенство![]() можно записывать в виде
можно записывать в виде![]() Для пределов последовательностей в
метрическом пространстве справедливы
утверждения:
Для пределов последовательностей в
метрическом пространстве справедливы
утверждения:
Теорема
1. Если
![]() существует, то он единственный.
существует, то он единственный.
Теорема
2. Всякая
сходящаяся последовательность
![]() являетсяограниченной
в том смысле,
что
являетсяограниченной
в том смысле,
что
![]()
Доказательства этих теорем проводятся совершенно аналогично соответствующим теоремам для обычных числовых последовательностей.
В нормированном пространстве Х справедлива теорема о пределе суммы:
Теорема
3. Если
![]() и
и![]() сходящиеся последовательности вХ
и
сходящиеся последовательности вХ
и
![]() R,
то последовательности
R,
то последовательности
![]() и
и![]() также сходятся и имеют место равенства
также сходятся и имеют место равенства![]()
![]()
Замечание.
В пространстве
![]() с метрикой (2) сходимость последовательности
с метрикой (2) сходимость последовательности![]() эторавномерная
сходимость.
Тот факт, что
эторавномерная
сходимость.
Тот факт, что
![]() в
в
![]() часто записывают в виде
часто записывают в виде![]()
Последовательность
![]() точек метрического пространстваХ
называется фундаментальной,
если
точек метрического пространстваХ
называется фундаментальной,
если
![]() (15)
(15)
Докажем,
что всякая
сходящаяся последовательность является
фундаментальной.
Действительно, пусть
![]() сходится
и
сходится
и
![]() Возьмём
любое
Возьмём
любое
![]() и подберём такое
и подберём такое![]() что
что![]() при
при
![]() Если теперь
Если теперь![]() то
то![]() т.е.
выполняется (15).
т.е.
выполняется (15).
Утверждение,
обратное к только что доказанному,
неверно, т.е. существуют метрические
пространства, в которых не все
фундаментальные последовательности
![]() сходятся. Примером может служить
последовательность
сходятся. Примером может служить
последовательность
1; 1,4; 1,41; 1,414; 1,4142 . . . (16)
(десятичные
приближения числа
![]() рассматриваемая как последовательность
точек метрического пространстваQ
рациональных
чисел. Действительно,
рассматриваемая как последовательность
точек метрического пространстваQ
рациональных
чисел. Действительно,
![]() при
при![]() поэтому
поэтому
![]() фундаментальна.
В то же время последовательность (16) не
имеет предела в Q,
так как
фундаментальна.
В то же время последовательность (16) не
имеет предела в Q,
так как
![]() не является рациональным числом.
не является рациональным числом.
Важный класс метрических пространств составляют так называемые полные пространства , имеющие большое значение для дифференциальных уравнений.
Определение. Метрическое пространство Х называется полным, если в нём всякая фундаментальная последовательность сходится.
Приведём примеры полных и неполных пространств.
Пространство R с обычной метрикой
 является полным. Действительно, в курсе
математического анализа был доказан
критерий Коши: последовательность
действительных чисел сходится в том и
только том случае, если она фундаментальна.
Это и означает полноту пространстваR.
является полным. Действительно, в курсе
математического анализа был доказан
критерий Коши: последовательность
действительных чисел сходится в том и
только том случае, если она фундаментальна.
Это и означает полноту пространстваR.Пространство Q с обычной метрикой – неполное пространство. Действительно, последовательность (16) точек из Q является фундаментальной, но не сходящейся.
Пространство R
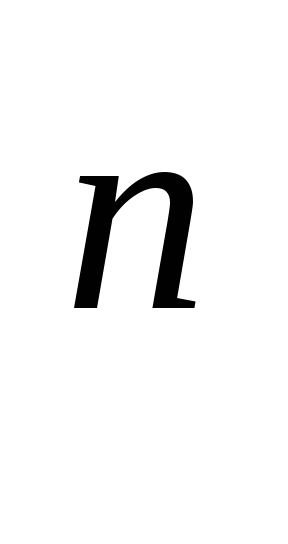 с любой
из метрик (5), (6), (7) полно. Приведём эскиз
доказательства этого утверждения для
метрики (5). Пусть
с любой
из метрик (5), (6), (7) полно. Приведём эскиз
доказательства этого утверждения для
метрики (5). Пусть
 и
и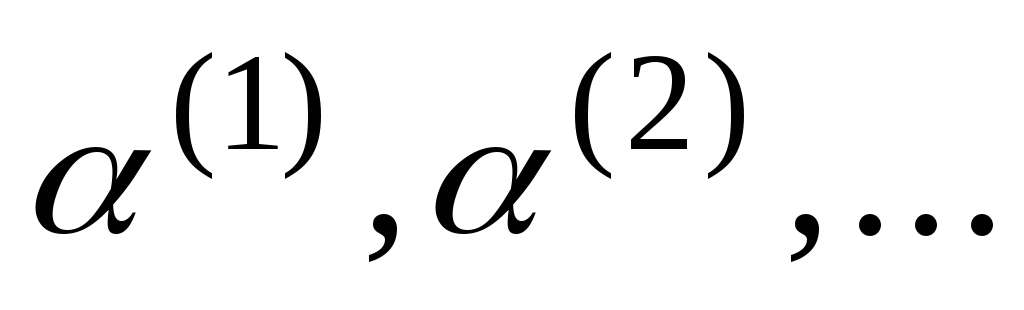 – фундаментальная последовательность
элементов изR
– фундаментальная последовательность
элементов изR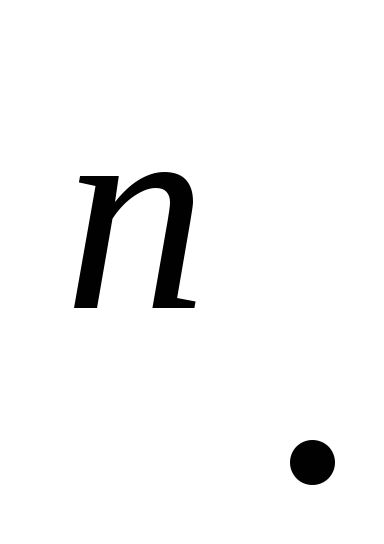 Тогда
Тогда
 где
где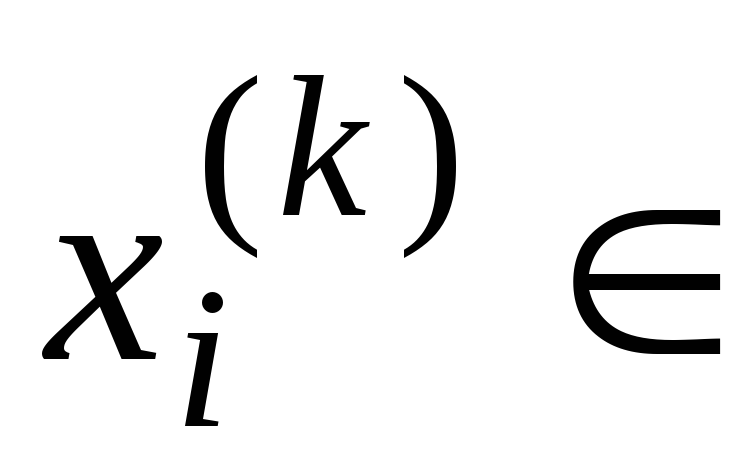 R.
Последовательность
R.
Последовательность
 составленную из
составленную из -х
координат векторов
-х
координат векторов очевидно, является фундаментальной
последовательностью действительных
чисел. Следовательно, она сходится.
Пусть
очевидно, является фундаментальной
последовательностью действительных
чисел. Следовательно, она сходится.
Пусть и
и Тогда
можно найти такие натуральные числа
Тогда
можно найти такие натуральные числа
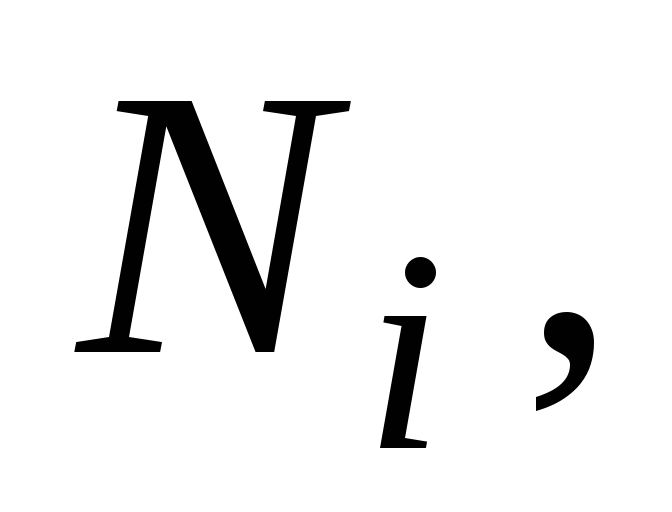 что
что при
при Взяв
Взяв получим, что
получим, что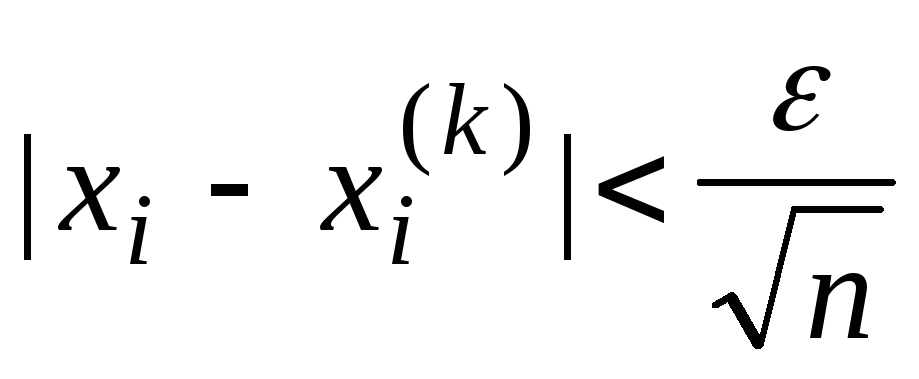 при
при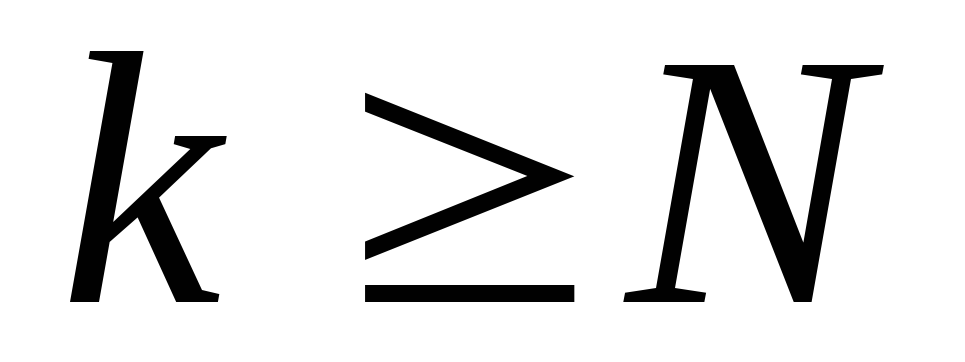 и
и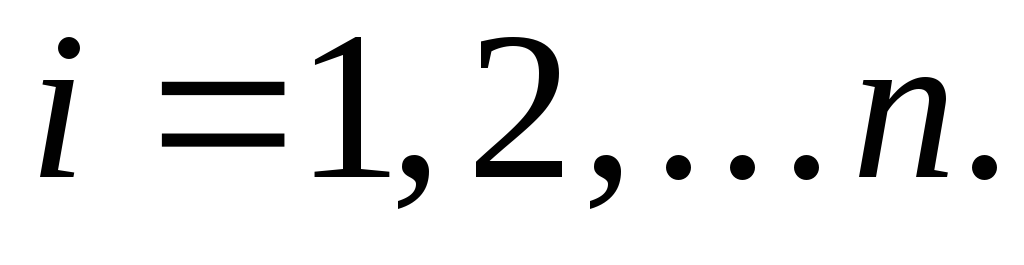 Отсюда
Отсюда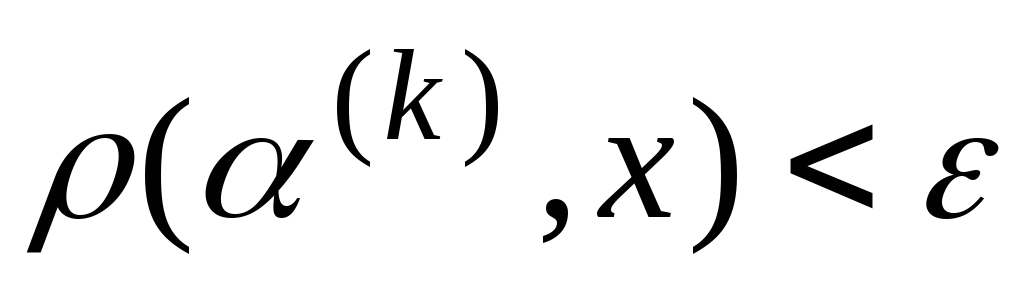 при
при
Пространство непрерывных функций
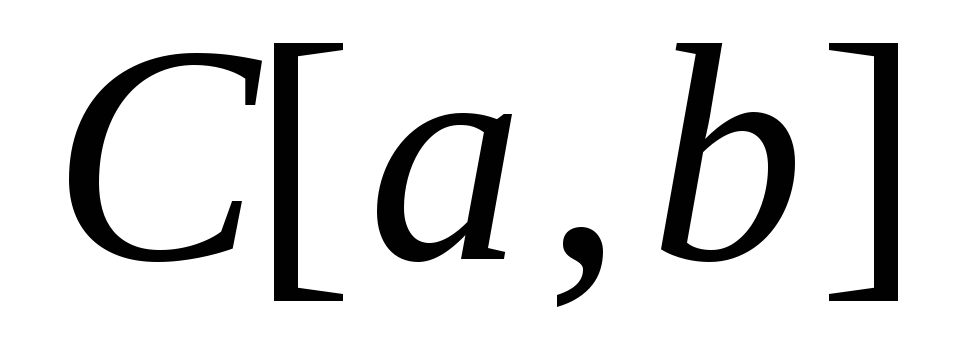 с метрикой (3) полное. Ввиду важности
этого результата для теории дифференциальных
уравнений отметим его в виде теоремы.
с метрикой (3) полное. Ввиду важности
этого результата для теории дифференциальных
уравнений отметим его в виде теоремы.
Теорема.
Пространство
![]() с метрикой
с метрикой
![]() является
полным.
является
полным.
Доказательство.
Пусть
![]() фундаментальная
последовательность в
фундаментальная
последовательность в![]() Разобьём доказательство на несколько
этапов.
Разобьём доказательство на несколько
этапов.
а)
Проверим, что для любой точки
![]()
![]() фундаментальная числовая последовательность.
Действительно, по условию
фундаментальная числовая последовательность.
Действительно, по условию![]() при
при![]() Поэтому
Поэтому![]() при
при![]()
б)
Найдём теперь функцию
![]() к которой последовательность
к которой последовательность![]() сходится равномерно. Выше было доказано,
что для каждого фиксированногох
последовательность
сходится равномерно. Выше было доказано,
что для каждого фиксированногох
последовательность
![]() сходится. Положим
сходится. Положим![]() Таким образом, последовательность
Таким образом, последовательность![]() сходится к
сходится к![]() поточечно
(в каждой
точке). Докажем теперь равномерную
сходимость. Для каждого
поточечно
(в каждой
точке). Докажем теперь равномерную
сходимость. Для каждого
![]() подберём натуральное число
подберём натуральное число![]() такое, что
такое, что
![]() при
при
![]() Из фундаментальности последовательности
Из фундаментальности последовательности![]() следует существование такого
следует существование такого![]() что
что![]() при
при![]() и всех
и всех![]() Следовательно, при
Следовательно, при![]() и любом
и любом
![]()
![]()
где
![]() Таким образом,
Таким образом,![]()
в)
Осталось показать, что предельная
функция
![]() принадлежит
принадлежит![]() т.е. является непрерывной. Пусть
т.е. является непрерывной. Пусть![]() произвольная
точка отрезка
произвольная
точка отрезка![]() По условию
По условию![]() при
при![]() и всех
и всех![]() Кроме того,
Кроме того,![]() при
при![]() Зафиксируем какое-нибудь
Зафиксируем какое-нибудь![]() и воспользуемся непрерывностью функции
и воспользуемся непрерывностью функции![]() в точке
в точке![]() Имеем:
Имеем:![]() Теперь
Теперь![]() при
при![]() что доказывает непрерывность функции
что доказывает непрерывность функции![]()
Назовём
вектор-функцией
![]() аргумента
аргумента![]() упорядоченный
набор
упорядоченный
набор
![]() обычных функций
обычных функций![]()
![]()
![]() фиксированное число. Пространство
фиксированное число. Пространство![]() всех непрерывных вектор-функций, т.е.
вектор-функций вида
всех непрерывных вектор-функций, т.е.
вектор-функций вида![]() ,
где
,
где![]() полное пространство относительно
метрики
полное пространство относительно
метрики
![]()
Полноту
этого пространства нетрудно доказать,
комбинируя доказательства полноты
пространств
![]() иR
иR![]()
Метрики
![]() и
и![]() на одном и том же множествеХназываютсяэквивалентными,
если существуют константы
на одном и том же множествеХназываютсяэквивалентными,
если существуют константы![]() такие, что
такие, что
![]()
Нетрудно
видеть, что сходимость в Хпоследовательности![]() не зависит от того, какая из эквивалентных
метрик
не зависит от того, какая из эквивалентных
метрик![]() выбрана. Следовательно, еслиХполно в метрике
выбрана. Следовательно, еслиХполно в метрике![]() то оно является полным и в метрике
то оно является полным и в метрике![]()
