Глава I. Общие сведения о дифференциальных уравнениях § 1. Дифференциальное уравнение и его решения. Основные понятия

Аппарат дифференциального исчисления, позволяет исследовать свойства данной функции – определять промежутки ее возрастания и убывания, скорость роста, точки максимума и минимума, направление и кривизну ее графика и пр. Часто приходится решать обратную задачу нахождения неизвестной функции по заданным ее свойствам. В простейших случаях эта задача сводится к нахождению первообразной. В других случаях для нахождения неизвестной функции по данным ее свойствам составляют уравнение, связывающее неизвестную функцию и величины, задающие ее свойства, и, поскольку эти последние выражаются через производные (или дифференциалы) того или иного порядка, приходят к соотношению, связывающему неизвестную функцию и ее производные или дифференциалы. Это соотношение называют дифференциальным уравнением. Решая его, находят искомую функцию, т. е. устанавливают закон, по которому происходит то или иное явление.

Порядкомдифференциального уравнения называется наивысший из порядков входящих в него производных. Все полученные выше дифференциальные уравнения были 1-го порядка. Если в уравнение входят неизвестная функция нескольких переменных и ее производные (частные производные), то уравнение называется уравнением в частных производных. Рассматривают также системы дифференциальных уравнений, содержащие несколько неизвестных функций. Мы будем изучать в первую очередь обыкновенные дифференциальные уравнения, содержащие одну неизвестную функцию одной независимой переменной; при этом начнем с уравнений 1-го порядка.

Обыкновенным дифференциальным уравнением 1-го порядка называется соотношение, связывающее независимое переменное, неизвестную функцию этого переменного и ее производную 1-го порядка.

Общий вид такого уравнения:

. (1)

Для краткости записи производные от пообозначаются штрихами.)

Решением дифференциального уравнения (1) мы будем называть всякую дифференцируемую функцию , удовлетворяющую этому уравнению, т. е. обращающую его в тождество (по крайней мере в некотором промежутке изменения); так что

.

Так, например, одним из решений, уравнения является функция();одним из решений уравненияслужит функция.

Общий вид дифференциального уравнения второго порядкаесть

, (2)

или, предполагая его разрешенным относительно второй производной (если это разрешение возможно),

. (2')

Здесь и– данные непрерывные функции своих аргументов,– независимое переменное,– искомая функция; некоторые из аргументов(или все они) могут не входить в уравнение, нанепременно входит. Решением опять называется функция , которая, будучи подставлена на местов уравнение (2) [или (2')], обратит его в тождество.

Дифференциальным уравнениемназывается уравнение, связывающее независимые переменные, их функцию и производные этой функции. Если независимых переменных две или более, то дифференциальное уравнение называетсяуравнением в частных производных, если независимая переменная одна, то уравнение называетсяобыкновенным.

Более точно, обыкновенным дифференциальным уравнением называется уравнение вида

(3)

где F ‑ известная функция;x‑ независимое переменное; ‑ неизвестная функция; ‑ее производная порядкаk .

Вообще порядком дифференциального уравненияназывается порядок наивысшей входящей в него производной от искомой функции. Так, уравнение-го порядка имеет вид:

,

причем непременно входит в уравнение.

Замечание.Вместо производных в дифференциальные уравнения могут входить дифференциалы.

Теорема о неявной функции. Пусть функциянепрерывна вместе со своей частной производнойв некоторой окрестности точки,причем, . Тогда найдутся такие окрестностиU_x  Rⁿ иU_y  R точек и, что для любой точки существует, и притом единственное, решение уравнения, причем это решение непрерывно наU_x и.

Если, кроме того, в некоторой окрестности точки существуют и непрерывны все частные производные, то в некоторой окрестности точкисуществуют и непрерывны частные производные.

Замечание.Теорема о неявной функции в теории обыкновенных дифференциальных уравнений, так же как и в математическом анализе, играет центральную роль, причем особенно интересен случай, получаемый следующим переобозначением независимых переменных:. Тогда,и теорема о неявной функции дает достаточные условия возможности сведения общего дифференциального уравнения (1) к дифференциальному уравнению, разрешенному относительно старшей производной.

Примеры обыкновенных дифференциальных уравнений:

1) ‑уравнение первого порядка, разрешенное относительно производной;

2) ‑уравнение первого порядка, не разрешенное относительно производной;

3) ‑уравнение второго порядка;

4) ‑ уравнение первого порядка, связывающее дифференциалы.

Примеры уравнений в частных производных:

;;;,

где – неизвестная функция.

Если уравнение, (1) разрешено относительно производной, то оно имеет вид:

.(4)

Частным случаем дифференциального уравнения (4) является уравнение вида:

. (5)

здесь непосредственно задается производная как данная функция от х.Решая эту задачу в интегральном исчислении, мы видели (предполагая, чтонепрерывна, а следовательно, интегрируема), что функции, являющиеся решениями уравнения (5), даются формулой:

или, что то же,

, (6)

где произвольная постоянная Спринимает любые значения отдо; причем при различных значенияхСмогут быть получены все функции, являющиеся решением уравнения (5). (обозначает произвольную первообразную функции,a ту из первообразных, которая приобращается в нуль).

Решение (6) является общим решениемдифференциального уравнения (5) и содержит одну произвольную постоянную (параметр):

, (7)

при этом при различных значениях Смогут быть получены все решения данного уравнения (быть может, лишь за некоторыми исключениями). Так, например, функциииявляются общими решениями дифференциального уравнения, а функция общим решением не является.

Решение, получаемое из общего решения при каком-либо фиксированном значении параметра, называется частным решением. Обычно для получения частного решения из общего требуют, чтобы искомая функция при некотором значениипринимала заданное значение. Из этих так называемыхначальных условийи определяется соответствующее значение параметра:

.

Вообще говоря, для точки , принадлежащей областиG, в которой задается дифференциальное уравнение,будет существовать решение, удовлетворяющее соответствующим начальным условиям: при, при этом такое решение будет единственным. Точка областиG, в которой единственность решения нарушается, т. е. либо нет решения, удовлетворяющего поставленным начальным условиям, либо этим начальным условиям удовлетворяет более чем одно решение (и, следовательно, заданием этих начальных условий частное решение однозначно не определяется), называетсяособой точкойдифференциального уравнения.

Так, например, дифференциальное уравнение имеет, как легко проверить, общее решение,причем начальному условию (при) удовлетворяют все частные решения, все они «проходят через точку» (0; 0). Точка (0; 0) является особой точкой этого дифференциального уравнения. (В этой точке, как это непосредственно видно, уравнение не устанавливает никакого соотношения междуи .)Та же точка (0; 0) является особой и для дифференциального уравнения:

имеющего общее решение , но по той же причине, что через нее не проходит графика ни одного решения; нет решения, удовлетворяющего начальным условиям: при.

Помимо общего решения и вытекающих из него частных решений, у дифференциального уравнения могут существовать решения, не получаемые из общего ни при каких значениях параметра. Так, у уравнения

кроме общего решения есть еще решенияи,не получаемые из общего ни при каком значении С.

Если каждая точка решения (не получаемого из общего) служит особой точкой дифференциального уравнения, то оно являетсяособымрешением .Если решение дифференциального уравнения получено в неявном виде:, или, то в этом случае его обычно называютинтегралом дифференциального уравнения, соответственно общим интегралом или частным интегралом. Для того чтобы не смешивать эти интегралы с интегралами функций (или), последние, по связи их с задачей вычисления площадей, называютквадратурами.

Операция нахождения общего решения или интеграла дифференциального уравнения называется интегрированием дифференциальных уравнений.

Всегда ли существует решение дифференциального уравнения (1)? Ответ на этот вопрос будет дан позже. Однако из того, что решение существует, еще не следует, что это решение мы можем выразить через элементарные функции и их интегралы, выразить в квадратурах. Такое решение в квадратурах возможно лишь в некоторых случаях.

Общее решение или общий интегралдифференциального уравнения с геометрической точки зрения представляют собой семейство кривых на плоскости (зависящее от одного параметраС); их называютинтегральными кривымидифференциального уравнения. Интегральная кривая дифференциального уравнения, таким образом, это график его решения (или интеграла); эта кривая непрерывна и имеет в каждой точке касательную. Само же дифференциальное уравнение,или (предполагая его разрешенным относительно производной)

,

о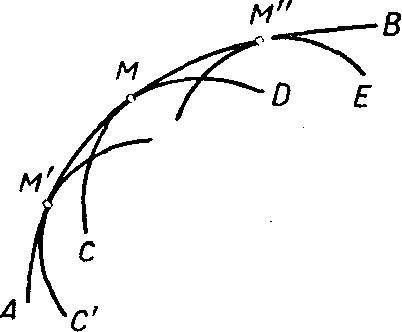тнося каждой паре значенийнекоторое значениеу',определяет в каждой точке плоскости или области , в которой задается дифференциальное уравнение, направление (точнее, угловой коэффициент касательной) кривой, проходящей через эту точку. Дифференциальное уравнение определяет, таким образом, поле направлений; •интегральные же кривые ‑ это кривые, имеющие в каждой своей точке направление, определяемое дифференциальным уравнением (направление поля). Решение дифференциального уравнения с этой точки зрения и состоит в нахождении кривой по заданному ее направлению (в каждой точке). Таких кривых не одна, а семейство. Чтобы выделить определенную кривую, нужно задать начальные условия, потребовать, чтобы кривая проходила через некоторую заданную точку ; и если эта точка не является особой точкой дифференциального уравнения, то через нее будет проходить единственная интегральная кривая.

Заметим, что если предположить, что семейство интегральных кривых имеет огибающую (Рис.1) (напомним, что огибающей называется кривая, в каждой своей точке касающаяся некоторой кривой семейства), то очевидно, что огибающая будет в каждой точке иметь направление, предписываемое дифференциальным уравнением, и, следовательно, будет также интегральной кривой. Поскольку в каждой точке огибающей нарушается условие единственности (кроме самой огибающей, через каждую ее точку проходит некоторая из огибаемыхею интегральных кривых'), то огибающая

Рис. 1 является графиком особого решения.

В уравнении общее решение изображается семейством кусков синусоид; решения жеи, не получаемые из общего, представляют огибающую этих кривых и, следовательно, являются особыми решениями (рис. 2).

Р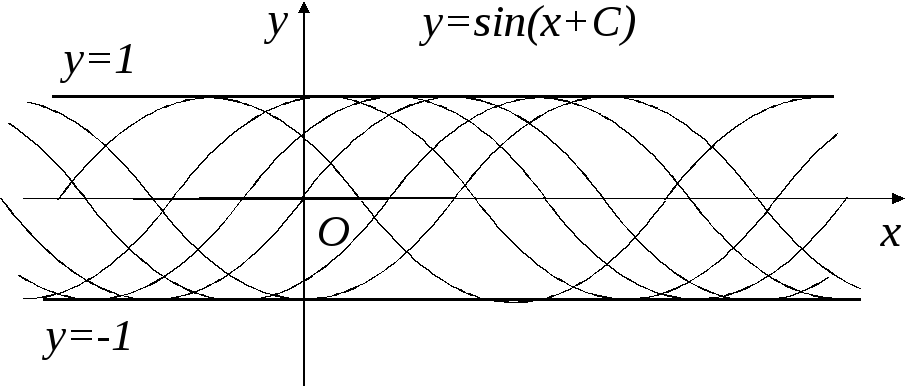ис. 2.