§ 5. Уравнения, не разрешенные относительно производной

Рассмотренные выше типы уравнений, интегрировавшихся в квадратурах, были уравнениями, разрешенными относительно производной. К уравнениям. не разрешенным относительно производной, в некоторых случаях оказывается применим метод введения параметра. Идея метода заключается в том, что в данном дифференциальном уравнении производнаярассматривается как параметр () и уравнение приобретает вид , и из данного уравнения выводится другое, с ним совместное (и содержащее произвольную постоянную): . Исключение параметрариз системы:

,(1)

приводит к общему интегралу данного уравнения .Если исключитьриз системы (1) фактически не удается, то может оказаться возможным, исключая из (1) поочередноуих,получить решение в параметрической форме:

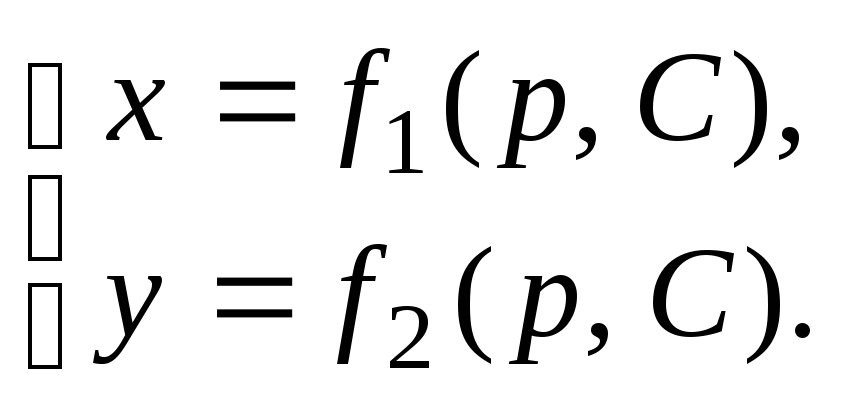(2)

Само получение из уравнения второго уравнения системы (1) производится путем его дифференцирования и последующего интегрирования. Однако в общем случае дифференцирование уравнения пох(или поу)приводит к соотношению между тремя переменнымих, у, ри(или), которое не интегрируется.

В том случае, когда данное дифференциальное уравнение может быть разрешено относительно х или относительноy, дифференцирование приведет к соотношению между переменнымих, ри(или переменнымиу, ри) т. е. к дифференциальному уравнению 1-го порядка, и притом разрешенному относительно производной. Так как переменные эти рассматриваются как равноправные, то достаточно ограничиться исследованием одного из этих случаев. В дальнейшем рассмотрим уравнения, разрешенные относительно функции:

. (3)

Согласно сказанному выше полагаем ,так что данное уравнение перепишется в виде:

. (4)

Дифференцируя данное уравнение по х[функция ,таким образом, предполагается дифференцируемой] и замечая, что,получаем:

. (5)

Отсюда

. (6)

Полученное уравнение является дифференциальным уравнением 1-го порядка с переменными х и р. Предполагая, что уравнение (6) интегрируется в квадратурах, находим его интеграл в виде:

. (7)

Исключение риз (4) и (7) приводит нас к общему интегралу данного уравнения (3). При этом, если уравнение (7) разрешимо относительнор:

,(8)

то, подставляя выражение для рв (4), получаем общее решение:

;(9)

если же уравнение (7) окажется разрешимым относительно х:

, (10)

то, подставляя значение хв (4), получаем: , что вместе с (10) дает общий интеграл данного уравнения в параметрической форме:

(11)

Замечание.В уравнении или нельзя рассматриватьркак производную с тем, чтобы далее находить общее решение данного уравнения интегрированием уравнения , ибо это значило бы искать решение не данного уравнения, а уравнение (второго порядка!), которое получено из данного путем его дифференцирования и которое ему не равносильно. Так, уравнениеимеет решение.Для уравнения жерешением служит.После того как (путем дифференцирования, а затем интегрирования) получено уравнение , отыскание решения производится без квадратур, а путем исключения параметра. Таким образом, в момент дифференцирования уравнения p еще не параметр, а производная и, следовательно, функция отх, и полученное дифференциальное уравнение является дифференциальным уравнением этой функциир. Но после того как это дифференциальное уравнение проинтегрировано, длярполучено конечное уравнение , и рассматривается система, в которойрподлежит исключению: с этого моментар считается параметром.