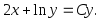Диф.уры Прокофьев / ГЛАВА2В
.DOC
Интегрирующий множитель. Если не
выполнено условие
![]()
![]()
![]() уравнение (1) уравнением в полных
дифференциалах не является. Возникает
мысль, нельзя ли такое уравнение
умножением на подходящий множитель
уравнение (1) уравнением в полных
дифференциалах не является. Возникает
мысль, нельзя ли такое уравнение
умножением на подходящий множитель
![]() ‑ такой множитель
называетcя интегрирующим
‑ превратить в уравнение
в полных дифференциалах?
‑ такой множитель
называетcя интегрирующим
‑ превратить в уравнение
в полных дифференциалах?
Для того чтобы функция
![]() была интегрирующим множителем, нужно,
чтобы произведение
была интегрирующим множителем, нужно,
чтобы произведение
![]()
было полным дифференциалом. Необходимым и достаточным условием этого является равенство:
![]() =
=![]() (15)
(15)
Выполняя дифференцирование, мы приходим к соотношению: .
![]() (16)
(16)
Соотношение (15) содержит неизвестную
нам функцию
![]() и ее частные производные, представляя,
таким образом, уравнение в частных
производных. Решение его, вообще говоря,
составляет задачу более сложную, чем
решение исходного уравнения.
и ее частные производные, представляя,
таким образом, уравнение в частных
производных. Решение его, вообще говоря,
составляет задачу более сложную, чем
решение исходного уравнения.
Замечание. В случае, если уравнение и имеет интегрирующий множитель (и даже бесконечное множество таких множителей), мы далеко не всегда умеем этот множитель найти и выразить с помощью квадратур.
Нахождение интегрирующего множителя проводится сравнительно просто, когда он является функцией одной переменной: либо х, либо у.
Положим, что нам известно, что данное
дифференциальное уравнение имеет
интегрирующий множитель, зависящий
только от х :
![]() .
В этом случае уравнение (16), определяющее
.
В этом случае уравнение (16), определяющее
![]() ,
значительно упростится:
,
значительно упростится:
![]()
или
![]() ,
,
откуда
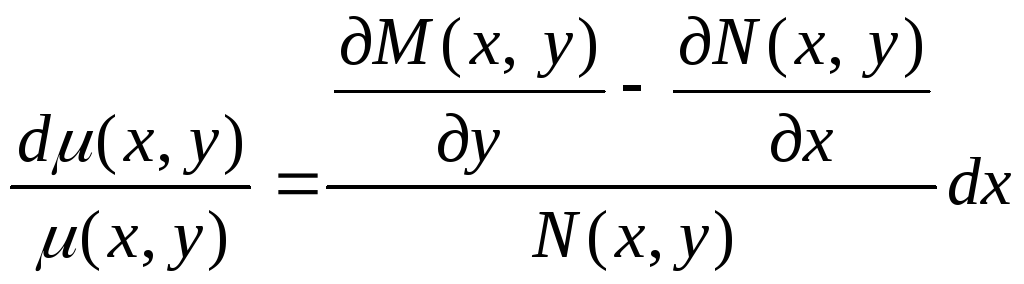 (17)
(17)
Так как по предположению
![]() зависит только от х, то только от х
зависит левая, а следовательно, и правая
часть равенства (17). Поэтому выражение
зависит только от х, то только от х
зависит левая, а следовательно, и правая
часть равенства (17). Поэтому выражение
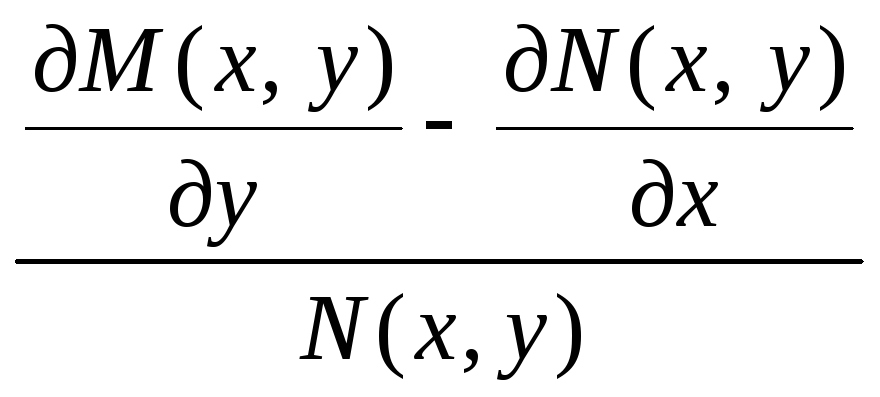 (18)
(18)
представляет функцию только х;
обозначая это выражение
![]() ,
мы из уравнения (17), интегрируя его,
находим
,
мы из уравнения (17), интегрируя его,
находим
![]() :
:
![]()
и, следовательно,.
![]() ,
где
,
где
 (19)
(19)
(мы берем одно из возможных значений
![]() ).
).
Наш вывод проведен в предположении, что заранее известно, что уравнение имеет интегрирующий множитель, зависящий только от х. Но как это узнать?
Докажем, что если выражение (18) зависит
только от х, то дифференциальное
уравнение имеет интегрирующий множитель
(19), зависящий от х. Чтобы показать
это, умножаем обе части уравнения
(1) на
![]() и проверяем выполнение условий (4):
и проверяем выполнение условий (4):
![]()
![]()
![]() .
.
Мы видим, что обе производные совпадают. Таким образом, доказано следующее предложение.
Теорема. Необходимым и достаточным
условием того, чтобы дифференциальное
уравнение M(x,y)dx+N(x,y)dy=0
имело интегрирующий множитель,
зависящий от х, является требование,
чтобы, выражение
![]() было функцией только х. В этом
случае интегрирующий множитель выражается
в квадратурах и может быть найден по
формуле:
было функцией только х. В этом
случае интегрирующий множитель выражается
в квадратурах и может быть найден по
формуле:
![]() .
.
Аналогичным образом
можно доказать, что если отношение
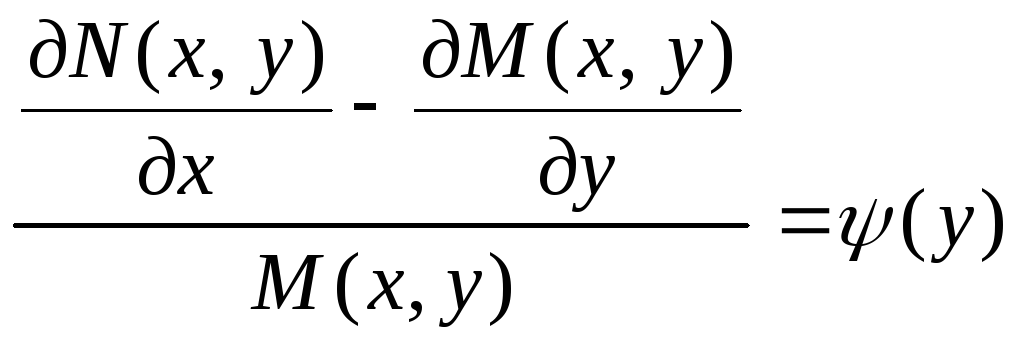 ‑ функция только от у, то
дифференциальное уравнение имеет
выражающийся в квадратурах интегрирующий
множитель:
‑ функция только от у, то
дифференциальное уравнение имеет
выражающийся в квадратурах интегрирующий
множитель:
![]()
зависящий только от у (см. ниже
упражнение 3); при этом условие
![]() является необходимым и достаточным,
чтобы уравнение M(x,y)dx+N(x,y)dy=0
имело такой интегрирующий множитель.
является необходимым и достаточным,
чтобы уравнение M(x,y)dx+N(x,y)dy=0
имело такой интегрирующий множитель.
Замечание. 1. Всякое однородное уравнение
M(x,y)dx+N(x,y)dy=0
умножением на
![]() превращается в уравнение в полных
дифференциалах.
превращается в уравнение в полных
дифференциалах.
2. Линейное уравнение имеет интегрирующий множитель, зависящий только от х.
5. Возникает естественный вопрос: не
нарушаем ли мы эквивалентности, умножая
дифференциальное уравнение на
интегрирующий множитель
![]() ?
?
Пользуясь интегрирующим множителем, мы превращаем левую часть данного уравнения в полный дифференциал некоторой функции:
![]() .
(23)
.
(23)
И затем, интегрируя уже уравнение dU = 0, получаем общий интеграл в виде: U(х,у)=С. Но из (23) следует, что
![]() (24)
(24)
Мы видим, что
![]() может обратиться в нуль не только
при dU=0, но и при
может обратиться в нуль не только
при dU=0, но и при
![]() .
Поэтому, если уравнение
.
Поэтому, если уравнение
![]() определяет у как некоторую функцию
от х (или х как
функцию от у), то эта функция является
решением дифференциального уравнения,
вообще говоря, не вытекающим из общего.
определяет у как некоторую функцию
от х (или х как
функцию от у), то эта функция является
решением дифференциального уравнения,
вообще говоря, не вытекающим из общего.
Так, для уравнения с разделяющимися
переменными
![]() решения, не вытекающие из общего, ищем
из равенства:
решения, не вытекающие из общего, ищем
из равенства:
![]() ,
,
что ранее было установлено из иных соображений.
С другой стороны, из (23) ясно, что если
уравнение
![]() определяет некоторую функцию у=f(x)
или х=g(y), то это
решение, входя в состав общего интеграла
уравнения dU=0, может оказаться
посторонним для данного дифференциального
уравнения.
определяет некоторую функцию у=f(x)
или х=g(y), то это
решение, входя в состав общего интеграла
уравнения dU=0, может оказаться
посторонним для данного дифференциального
уравнения.
Разбор типовых примеров
1.
![]()
Решение:
![]()
Попытаемся найти
интегрирующий множитель, зависящий
только от х,
исходя из соотношения
![]()
![]() ‑ зависит только
от х,
значит,
‑ зависит только
от х,
значит,
![]() (положим,
(положим,
![]() )
)
![]()
При х
= 0
(х) не
определено. Поэтому функцию х=0
проверяем отдельно. Подстановка
показывает, что х=0
является интегралом исходного
дифференциального уравнения. Умножая
на
![]() обе части данного уравнения, получим
уравнение в полных дифференциалах:
обе части данного уравнения, получим
уравнение в полных дифференциалах:
![]()
![]()
Ответ:
![]()
2.
![]()
![]()
Решение:
![]()
 (не зависит
только от х
).
(не зависит
только от х
).
![]() (
зависит только от у
).
(
зависит только от у
).
Тогда
![]() ,
у= 0 ‑
отдельное решение.
,
у= 0 ‑
отдельное решение.
![]() (при
у
0).
(при
у
0).
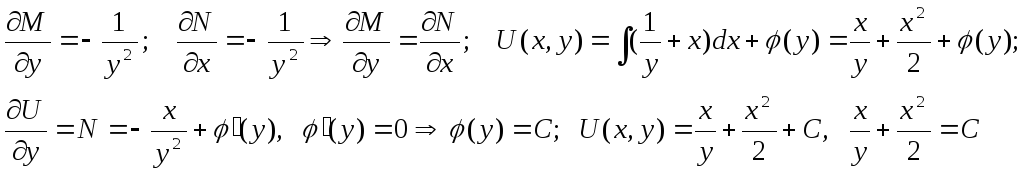
Ответ:
![]()
3.
![]()
Решение:
![]()
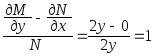 (можно
рассматривать как зависимость от х).
(можно
рассматривать как зависимость от х).

![]()


![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
Задачи для самостоятельного решения
1.
![]() Ответ:
Ответ:
![]()
2.
![]() Ответ:
Ответ:
![]()
3.
![]() Ответ:
Ответ:
![]()
4.
![]() Ответ:
Ответ:
![]()
5.
![]()
Ответ:
![]()
6.
![]() Ответ:
Ответ:
![]()
-
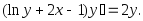 Ответ:
Ответ: