§3. Геометрическое истолкование дифференциального уравнения. Метод изоклин.

С геометрической точки зрения дифференциальное уравнение , которому удовлетворяют все кривые, выражает некоторое общее свойство этих интегральных кривых, и притом свойство, их характеризующее (ибо по дифференциальному уравнению эти кривые могут быть найдены).

С этой точки зрения приобретает интерес обратная задача: по уравнению семейства кривых (или вообще функций) (конечному уравнению) найти дифференциальное уравнение, которому эти кривые (функции) удовлетворяют; это дифференциальное уравнение (не содержа параметра) будет выражать некоторое общее, характерное свойство кривых (функций).

Поставим задачу, в некотором смысле обратную задаче интегрирования дифференциального .уравнения. Пусть дано соотношение:

, (1)

где есть параметр; дифференцируя по(мы предполагаем, что все входящие в рассуждения производные существуют), получим:

. (2)

Если правая часть выражения (2) не содержит , то мы уже произвели исключение параметраи получили дифференциальное уравнение:

; (2')

очевидно, что в этом случае соотношение (1) имеет вид:

и является решением уравнения (2').

Пусть теперь правая часть равенства (2) содержит ; тогда правая часть равенства (1) содержит, т. е., и в окрестности значенийдля которых, мы можем определитькак функцию оти:

. (3)

Очевидно, что имеет место тождество (по переменным и):

. (4)

Подставляя значение , определённое формулой (3), в выражение (2), мы получим дифференциальное уравнение первого порядка:

. (5)

Легко убедиться в том, что (1) представляет его решение при любом значении ; в самом деле, если мы подставим это выражение дляв уравнение (5), то в левой части получим , а в правой , а это, в силу тождества (4), тоже дает .

Если соотношение между дано в неявном виде:

, (6')

то, дифференцируя его по ,находим:

(6'')

Исключая из соотношений (6') и (6"), приходим, при выполнении соответствующих условий из теории неявных функций, к уравнению

. (7)

Предыдущие рассуждения показывают, что (6') определяет его решение.

Пусть теперь дано соотношение

, (8)

связывающее функцию и независимое переменноеи заключающеепараметров. Нельзя ли построить дифференциальное уравнение, которому удовлетворяет функция, определенная соотношением (8), при любых постоянных значениях параметров? Мы предположим, чтонепрерывна по всем аргументам и дифференцируема ноидостаточное число раз. Дифференцируем в указанных предположениях равенство (8)раз [оно является тождеством, если вместоподставить функцию, определяемую соотношением (8)]. Имеем:

(9)

Соотношения (8) и (9) образуют систему уравнений; они содержатпараметров .Вообще говоря из этой системы можно исключить все параметры, т. е. найти их выражения черезизуравнений и вставить эти выражения в ()-е уравнение. Приходим к соотношению вида:

, (10)

т. е. к дифференциальному уравнению -го порядка. Мы уже отметили, что при подстановке в уравнение (8) на местоуего выражения получается тождество, и то же справедливо; относительно уравнений (19); поэтому и уравнение (10), являются следствием уравнений (8) и (9), обратится в тождество, если в подставить вместоуфункцию , а это значит, чтоу, определяемый из уравнения (8), есть решение уравнения Таким образом, эта функция, содержащаяпроизвольных постоянных, является решением некоторого дифференциального уравнения-го порядка. Можно было бы провести и более точное рассуждение как это было сделано для уравнения первого порядка. Теперь можно ожидать, что исходное решение является общим и что, обратно, общее решение дифференциального уравнения-го порядка содержитпроизвольных постоянных.

Метод изоклин.Дифференциальному уравнению первого порядка можно дать геометрическое толкование, которое выяснит нам вопрос о характере множественности решений такого уравнения. Пусть дано уравнение в виде:

. (9)

Примем за декартовы прямоугольные координаты плоскости. Каждой точкетой области, где определена функция, уравнение (9) ставит в соответствие определенное значение. Пусть есть решение уравнения (9); тогда кривая, определяемая уравнением , называетсяинтегральной кривойдифференциального уравнения. Значениеесть тангенс угла, образуемого касательной к этой кривой с осью. Таким образом, каждой точкерассматриваемой области уравнение (9) ставит в соответствие некоторое направление; мы получаемполе направлений. Это поле можно изобразить, поместив в соответствующих точках областистрелки, образующие с осьюуглы(положительное направление стрелки можно взять произвольным, так как арктангенс определяет угол лишь с точностью до кратного). Задача интегрирования дифференциального уравнения может быть теперь истолкована так: найти такую кривую, чтобы ее касательная в каждой точке имела направление, совпадающее с направлением поля в этой точке, т.е. нужно провести кривую так, чтобы расставленные на поле стрелки показывали в каждой точке направление касательной к искомой кривой.

Рассмотрим подробнее следующий пример.

Пример.Построить графически интегральные кривые уравнения:

. (11)

Решение. Построим поле направлений, найдя предварительно те линии, где наклон интегральных кривых одинаков (изоклины), из условия. Получим уравнение семейства изоклин

.

Т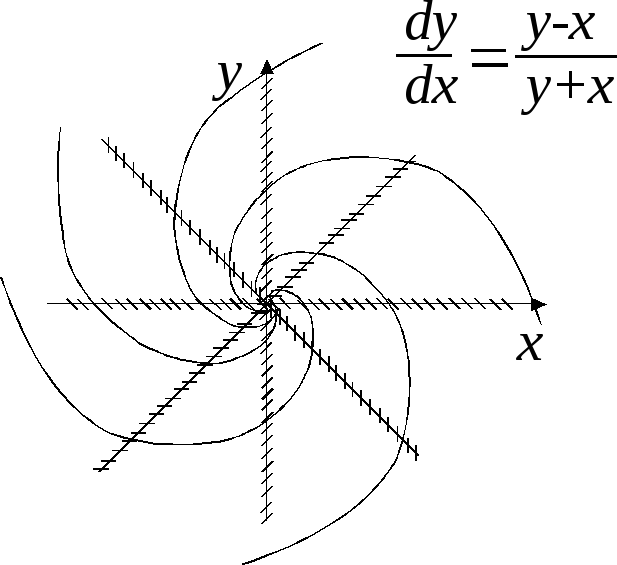аким образом, изоклинами являются прямые, проходящие через начало координат.

Рис. 1.

При получим изоклину, при‑ изоклину, при‑ изоклину. Рассматривая «перевернутое» уравнение, найдем ‑ изоклину, во всех точках которой интегральные кривые имеют вертикальные касательные.

В точке (0, 0) пересекаются все изоклины данного уравнения (особая точка уравнения). С помощью полученных изоклин строим интегральные кривые (рис. 1).

Мы видим, что получается не одна кривая, а целое семейство. Аналогично для любого поля, т. е. любого дифференциального уравнения: интегральные кривые дифференциального уравнения первого порядка образуют семейство, зависящее от одного параметра:

.

Замечая, что функция при любоместь решение дифференциального уравнения, мы можем также ожидать следующего результата:общее решение дифференциального уравнения первого порядка дается формулой ,заключающей одно произвольное постоянное.

Наконец, вспомнив, что мы получаем каждую отдельную интегральную кривую, задавая точку , через которую она проходит, мы приходим к следующему заключению:

Чтобы однозначно определить частное решение дифференциального уравнения первого порядка, надо задать то значение , которое искомая функция принимает при заданномзначении , независимого переменного(начальные значения).

В самом деле, если иданы, то подставляя их в уравнение (12), мы получим:– одно уравнение для определения одного неизвестного; наши геометрические соображения позволяют ожидать, что это уравнение имеет решение.

Примечание.Рассуждения настоящего раздела не являются строгими доказательствами существования решения дифференциального уравнения и однозначного определения частного решения начальными данными, так как они ссылаются на геометрическую картину; все приведенные результаты справедливы лишь при определенных ограничениях, наложенных на функцию. Проведенные рассуждения только дают практический прием для приближенного вычерчивания интегральных кривых.

Рассмотрим задачу о нахождении ортогональных траекторий. Изогональной траекториейсемейства кривых называется кривая, пересекающая все кривые данного семейства под одним и тем же углом.

Если,то траектория ортогональна (рис. 2). Изогональные траектории также составляют некоторое семейство кривых. Данное семейство кривых и его ортогональные траектории взаимно ортогональны.

Если – дифференциальное уравнение данных кривых, то нетрудно понять, что дифференциальное уравнение ортогональных траекторий получается из него заменой в немна:.

Рис. 2.

Интегрируя это дифференциальное уравнение, получаем конечное уравнение ортогональных траекторий. Если данные кривые заданы конечным уравнением, то предварительно следует получить их дифференциальное уравнение так, как показано выше.

Пример.Найти ортогональные траектории семейства парабол.

Дифференциальное уравнение семейства парабол имеет вид:

.

Дифференциальное уравнение ортогональных траекторий находим, заменяя на:

Интегрируя его, получаем:

, или .

Ортогональные траектории представляют собой семейство эллипсов с отношением осей (рис. 3).

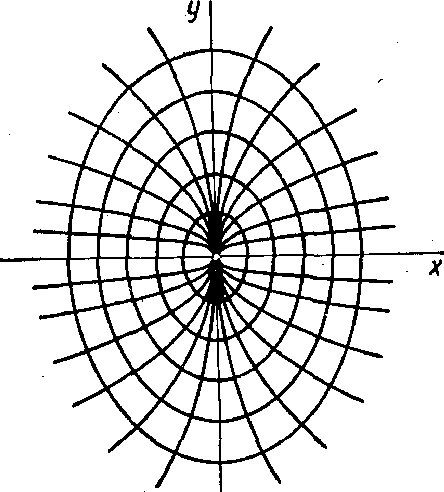
Рис. 3.

Дифференциальному уравнению 1-го порядка можно дать и механическое истолкование. Обозначив независимое переменное через ,а функцию через,мы скажем, что дифференциальное уравнение

выражает соотношение, существующее в некотором прямолинейном движении в каждый момент времени между пройденным путеми скоростью движения . Решение выражает закон движения, задает путь как функцию от времени ,при этом начальные условиядают положение движущейся точки в начальный момент.