5.3.2. Частотные характеристики сау

Наряду с методом временных характеристик в теории автоматического управления широко используются методы частотных характеристик, которые определяют поведение системы при подаче на ее вход гармонических колебаний.

Если на вход системы (или отдельного звена) подавать гармонические (синусоидальные) колебания с постоянной амплитудой f_о и частотой ₁

, где ,

то после затухания переходных процессов на выходе также возникнут синусоидальные колебания

с той же частотой ₁, но с другой амплитудой , сдвинутые по фазе на величину₁ относительно входных колебаний (рис.), где .

Начертим в декартовой системе координат Р() , Q() вектор, начало которого совпадает с началом координат, модуль (длина вектора) равен , а аргумент (угол между положительным направлением оси абсцисс и данным вектором, причем положительное направление угла откладывается против часовой стрелки) равен углу₁ (обычно ₁ отрицательно). У конца вектора сделаем отметку ₁ (рисунок).

Изменим теперь частоту  колебаний, подводимых на вход системы, не меняя их амплитуды. Пусть =₂. Тогда и на выходе установятся колебания частоты ₂:

Построим на графике вектор с модулем , аргументом –₂ и отметкой ₂.

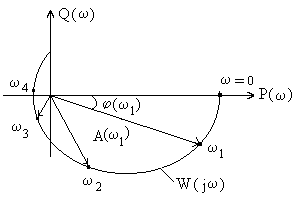
Аналогично повторив эксперимент при новом значении  = ₃, построим на этом же рисунке вектор с отметкой ₃ и т.д. для разных значений  от  = 0 до  =  (практически до достаточно больших ) и соединим плавной линией концы этих векторов. Построенная таким образом кривая называется амплитудно–фазовой характеристикой (АФХ) или комплексной частотной характеристикой (КЧХ) линейной системы W(j).

Кривая зависимости от называется амплитудно–частотной характеристикой системы А() , а кривая зависимости  от  – ее фазочастотной характеристикой ().

Обозначим через Р() и Q() проекции вектора АФХ на оси абсцисс и ординат. Кривые зависимости Р и Q от  называются соот­ветственно вещественной (действительной) и мнимой частотными характеристиками системы.

Частотные характеристики могут быть получены и расчетным путем – по передаточной функции системы W(p). Приведем соответствующую методику без доказательств.

Пусть передаточная функция системы W(p) представлена в виде:

.

Придадим оператору р чисто мнимое значение р = j, и получаем

Представим числитель и знаменатель W(j) в виде комплексных выражений:

где B() = b_о – b₂ ² + b₄ ⁴ – …, C() = b₁  – b₃ ³ + b₅ ⁵ –…,

M() = a₀ – a₂ ² + a₄ ⁴ – …, N() = a₁ – a₃ ³ + a₅ ⁵ – …

Освобождаясь от мнимости в знаменателе, получим:

где – вещественная частотная характеристика системы;

–мнимая частотная характеристика системы.

Р() и Q() соответствуют аналогичным функциям, рассматривавшимся при экспериментальном определении W(j), т.е. это проекции вектора АФХ на оси абсцисс и ординат.

Для вполне определенной частоты ₁ в декартовой системе координат функции W(j₁ ) соответствует точка с координатами Р(₁) и Q (₁), являющаяся концом вектора, проведенного из начала координат (рис.).

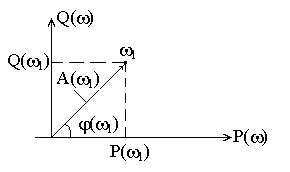
Но с другой стороны, любой вектор можно задать его полярными координатами (модулем и аргумен–том), т.е. где– амплитудно–частотная характеристика при = ₁;– фазочастотная характеристика при = ₁. Таким образом, амплитудно–фазовая характеристика W(j) может быть задана функциями Р() и Q() либо характеристиками А(), ():

.

Дадим определения всем указанным характеристикам.

Амплитудно–фазовой характеристикой (АФХ) называется зависимость отношения выходной величины системы к входной величине, выраженного в комплексной форме, от частоты в установившемся режиме.

Амплитудно–частотной характеристикой (АЧХ) называется зависимость от частоты отношения амплитуды синусоидальной величины на выходе звена к амплитуде синусоидальной величины на входе.

Фазочастотной характеристикой (ФЧХ) называется зависимость разности фаз синусоидальных колебаний на выходе и входе системы.

Вещественной частотной характеристикой (ВЧХ) называется зависимость величины проекции АФХ на вещественной оси Р() от частоты входного синусоидального воздействия.

Мнимой частотной характеристикой (МЧХ) называется зависимость величины проекции АФХ на мнимой оси Q() от частоты входного синусоидального воздействия.

Литература

1. Львовский Е. Н. Статистические методы построения эмпирических формул. М.: Высшая школа, 1988.

2. Щиголев В. М. Математическая обработка наблюдений. М.: Изд. «Наука», 1969.

3. Гмурман В. Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 2005.

4. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1975.

5. Ерофеев А. А. Теория автоматического управления. Санкт–Пет.: «Политехника, 2001.

Оглавление

Тема 1. Случайные события и случайные величины, их числовые характеристики 1.1. Математические модели эксперимента, учитывающие случайный разброс его результатов 1.2. Случайные события 1.3. Случайные величины 1.4. Примеры законов распределения случайной величины Тема 2. Точечное оценивание параметров. Регрессионный и корреляционный анализ 2.1. Выборочный метод 2.2. Связь между случайными величинами. Корреляция 2.3. Регрессия Тема 3. Проверка статистических гипотез и построение доверительных областей для параметров 3.1. Доверительные интервалы и доверительные вероятности 3.2. Оценка генерального среднего 3.3. Оценка генеральной дисперсии 3.4. Проверка статистических гипотез 3.5. Проверка адекватности уравнения регрессии (математической модели) Тема 4. Математическое описание случайных сигналов в системах управления 4.1. Случайные процессы 4.2. Стационарные случайные процессы 4.3. Корреляционная функция 4.4. Спектральная плотность Тема 5. Понятие передаточной функции и частотных характеристик системы 5.1. Элементы операционного исчисления. Преобразование Лапласа 5.2. Понятие передаточной функции 5.3. Временные и частотные характеристики САУ Литература

3  5 10 21 26 26 29 35 48  49 53 54 59 61  64 66 69 71  77 79 87

91