3.5. Проверка адекватности уравнения регрессии

(математической модели)

После завершения вычислений, связанных с получением оценок коэффициентов регрессии, проверяется адекватность полученного уравнения.

Для проверки значимости (адекватности) уравнения регрессии в целом с использованием F–критерия Фишера общую дисперсию сравнивают с остаточной дисперсией.

Общая дисперсия У:

,

где n – объем выборки; у_i (i = 1, 2,…, n) – выборочные значения у.

Остаточная дисперсия (дисперсия неадекватности)

,

т.е. показатель ошибки предсказания уравнением регрессии результатов опытов, где у_рi – расчетное значение величины у, вычисленное по полученному уравнению регрессии (двойка в знаменателе) – количество переменных в уравнении регрессии.

Качество предсказания определяют, сравнивая с. Находят(делят всегда большую величину на меньшую).

Для заданной величины уровня значимости по таблице критерия Фишера (и для соответствующих значений степеней свободыf₁ и f₂) определяют табличное значение критерия F_таб.

Для того, чтобы уравнение регрессии адекватно описывало результаты экспериментов с определенной доверительной вероятностью «р» требуется выполнение следующего условия: F < F_таб.

Пример. Данные эксперимента

№ п/п	х	у
1	1,5	5,0
2	4,0	4,5
3	5,0	7,0
4	7,0	6,5
5	8,5	9,5
6	10,0	9,0
7	11,0	11,0
8	12,5	9,0
	59,5	61,5

Расчеты по известной методике позволяют получить для уравнения регрессии  = 3,73;  = 0,53, т.е. линейное уравнение регрессии имеет вид:

.

Оценим значимость этого уравнения с использованием критерия Фишера. Для этого определяем общую дисперсию у:

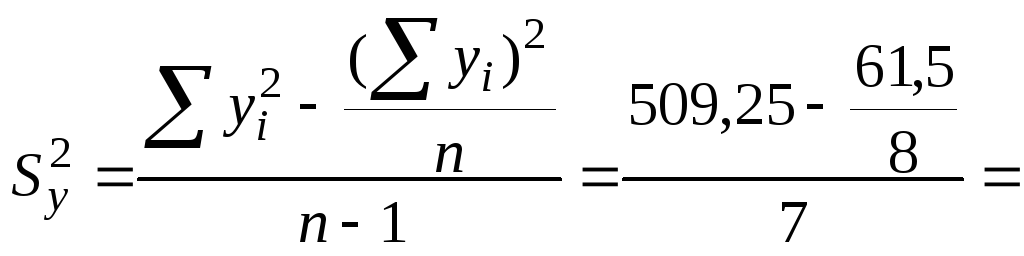
(при этом ивзяты из таблицы, по которой определяют коэффициенты регрессии).

Остаточная дисперсия и находится с помощью таблицы

№ п/п	yi	xi	ypi = 3,73 + 0,53xi	yi – ypi	(yi – ypi)2
1	5,0	1,5		+0,47	0,2209
2	4,5	4,0		–1,35	1,82225
3	7,0	5,0		+0,62	0,3844
4	6,5	7,0		–0,94	0,8836
5	9,5	8,5		+1,26	1,5876
6	9,0	10,0		–0,03	0,0009
7	11,0	11,0		+1,44	2,0736
8	9,0	12,5		–1,35	1,8225
	61,5	59,5		0,12	8,8

Откуда

.

Определяем

.

Для 5 % уровня значимости ( = 0,05) и для f₁ = 7, a f₂ = 6, F_таб = 4,21

F < F_таб, т.е. уравнение регрессии адекватно.

Тема 4. Математическое описание случайных сигналов в системах управления

4.1. Случайные процессы

Функция, значение которой при каждом данном значении независимой переменной является случайной величиной, называется случайной функцией. То есть, это бесконечная совокупность случайных величин, зависящая от непрерывно изменяющейся независимой переменной. Случайная функция, зарегистрированная по результатам опыта, называется реализацией случайной функции. Случайная функция, для которой независимой переменной является время t называется случайным (стохастическим) процессом.

Для характеристики случайной функции служат моменты случайной функции. Для их определения необходимо знать многомерные функции распределения случайной величины.

Предположим, что мы располагаем большим числом однотипных систем, работающих одновременно при одинаковых условиях. Будем наблюдать изменения величин на выходе этих устройств. Они будут характеризоваться некоторыми случайными функциями причем все эти функции будут отличаться друг от друга.

Рассмотрим какой–либо момент времени t и найдем, какая доля из общего числа функций x(t) имеет в этот момент времени значение, заключенное между х и x + dx.

Эта доля зависит от момента времени t и пропорциональна dx при малых dx. Обозначим ее через w₁(х, t)dx – (при количестве реализаций, стремящихся к бесконечности, эта величина соответствует вероятности того, что в момент времени t величина х будет заключена в пределах х и х + dх) и назовем w₁(х, t) – первой или одномерной функцией распределения вероятности.

Рассмотрим теперь все возможные пары значений х, наблюденные в два различных момента времени t₁ и t₂. Долю пар значений х, для которой величина х заключена между (х₁, х₁+ dх₁) при t = t₁ и между (х₂, х₂ + dх₂) при t = t₂, отнесенную к общему числу наблюденных пар значений, обозначим через w₂(х₁, t₁, х₂, t₂)dx₁dx₂ и назовем второй или двумерной функцией распределения вероятности.

Этот процесс можно продолжить и определить третью, четвертую и все последующие функции распределения вероятности.

Итак, случайный процесс можно характеризовать некоторыми функциями распределения вероятности, полностью определяющими его в статистическом смысле.

Действительно, зная w₁(х, t) можно определить математическое ожидание m_ox(t) случайной величины х(t):

и его дисперсию _2х(t):

.

Зная вторую функцию распределения w₂(х₁,t₁, х₂,t₂), можно определить как m_ox(t), _2х(t), так и центральный момент 2–го порядка:

,

характеризующий связь между значениями случайной функции в различные моменты времени. Функция _2х(t₁,t₂) называется корреляционной функцией.

Зная n–мерную функцию распределения вероятности, можно определить все последующие моменты случайной функции, включая момент n–го порядка.

Если приходится иметь дело не с одной, а с несколькими взаимосвязанными функциями, то кроме их собственных моментов, приходится вводить еще и их взаимные моменты.

Так, например, если имеются две случайные функции х(t) и y(t), то простейшим взаимным моментом является момент 2–го порядка:

=

называемый взаимной корреляционной функцией случайных процессов х(t) и y(t).