5. Базис в пространстве. Теорема о разложении любого вектора по трем базисным векторам.

Любой вектор ЛП разлагается, причем единственным образом в ЛК базисных векторов этого пространства.

Док-во:Рассмотрим ЛП размерностью n с базисом l₁, l₂, ... ,l_n, вектор а Є ЛП. Система векторов l₁, l₂, ... ,l_n, а, отсюда следует, что система ЛЗ, т.е. линейная комбинация α₁ l₁+ α₂ l₂+ ... +α_nl_n+α_n+1a = 0, есть ≠ 0 коэффициент.

Покажем, что коэффициент α_n+1 ≠ 0 от противного. Допустим, что α_n+1 = 0, тогда α₁ l₁+ α₂ l₂+ ... +α_nl_n+0 a = 0, отсюда следует, что α₁ l₁+ α₂ l₂+ ... +α_nl_n= 0 и есть ≠ 0 коэффициент.

Получили противоречие тому, что базис l₁, l₂, ... ,l_n- ЛНЗ, отсюда следует α_n+1 ≠ 0.

Следовательно, мы доказали, что коэффициент α_n+1 ≠ 0.

Разделим на коэффициент α_n+1.

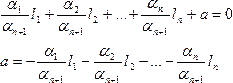
отсюда следует, что вектор а - ЛК базисов.

Докажем единственность разложения базиса от противного.

Пусть есть два разложения вектора а по базису.

a = α₁ l₁+ α₂ l₂+ ... +α_n l_n

a = β ₁ l₁+ β ₂ l₂+ ... + β _nl_n

0 = (α₁- β₁) l₁+ (α₂- β₂) l₂+ … + (α_n- β_n) l_n, т.к. базис - ЛНЗ, то коэффициенты α₁- β₁=0, α₂- β₂=0, α_n- β_n=0, отсюда следует α₁=β₁, α₂=β₂ , α_n=β_nкоэффициенты совпали. Единственность разложения доказана.

6. Линейная зависимость векторов.

Определение 10.14   Система векторов называется линейно зависимой, если существует такой набор коэффициентов, из которых хотя бы один отличен от нуля, что.

Система векторов, которая не является линейно зависимой, называется линейно независимой. Но последнее определение лучше сформулировать по другому.

Определение 10.15   Система векторов называется линейно независимой, если равенствовозможнотолько при .

Кто плохо понял два последних определения, может получить дополнительные объяснения здесь.

Предложение 10.6   Система векторов линейно зависима тогда и только тогда, когда один из векторов системы является линейной комбинацией остальных векторов этой системы.

        Доказательство.     Пусть система векторов линейно зависима. Тогда существует такой набор коэффициентов , что, причем хотя бы один коэффициент отличен от нуля. Предположим, что. Тогда

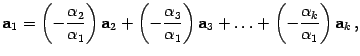
то есть является линейной комбинацией остальных векторов системы.

Пусть один из векторов системы является линейной комбинацией остальных векторов. Предположим, что это вектор , то есть. Очевидно, что. Получили, что линейная комбинация векторов системы равна нулю, причем один из коэффициентов отличен от нуля (равен).

Предложение 10.7   Если система векторов содержит линейно зависимую подсистему, то вся система линейно зависима.

        Доказательство.    

Пусть в системе векторов подсистема,, является линейно зависимой, то есть, и хотя бы один коэффициент отличен от нуля. Тогда составим линейную комбинацию . Очевидно, что эта линейная комбинация равна нулю, и что среди коэффициентов есть ненулевой.

Упражнение10.4.1. Докажите, что если система векторов линейно независимая, то любая ее подсистема линейно независимая.     

Предложение 10.8   Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.

        Доказательство.     Пусть система состоит из вектора . Линейная комбинация имеет вид. Если, то, то есть система линейно зависима. Еслии, то.

        Предложение 10.9   Система, состоящая из двух векторов, линейно зависима тогда и только тогда, когда эти векторы коллинеарны.

        

Доказательство этого предложения предоставляется читателю. Оно аналогично доказательству следующего предложения.

Предложение 10.10   Система из трех векторов линейно зависима тогда и только тогда, когда эти векторы компланарны.

        Доказательство.     Пусть векторы -- компланарные. Если-- коллинеарные, то в силу предыдущего предложения они образуют линейно зависимую подсистему системы. Попредложению 10.7 система -- линейно зависима. Если векторы-- неколлинеарные, то попредложению 10.2 является линейной комбинацией векторови попредложению 10.6 система векторов -- линейно зависимая.

Пусть система векторов линейно зависима. По  предложению 10.6 один вектор, скажем , является линейной комбинацией других векторов,и,. Правая часть последнего равенства лежит в плоскости, в которой лежат векторы. Поэтому векторлежит в одной плоскости с векторами, то есть векторы-- компланарные.

Предложение 10.11   Четыре вектора всегда образуют линейно зависимую систему.

        Доказательство.     Если первые три вектора являются компланарными, то они образуют линейно зависимую подсистему ( предложение 10.10). Следовательно, вся система линейно зависима ( предложение 10.7). Если первые три вектора -- некомпланарные, то четвертый является их линейной комбинацией ( предложение 10.3). По  предложению 10.6 система является линейно зависимой.     

На основании сказанного дадим другое определение базиса, которое является более распространенным, чем  определение 10.12.

Определение 10.16   Базисом векторного пространства называется такая упорядоченная линейно независимая система векторов, что любой вектор пространствараскладывается по векторам этой системы.

Из  предложений 10.8 – 10.11 следует, что это определение эквивалентно определению 10.12.