2.2. Кинематика твердого тела

Различают несколько видов механического движения твердого тела: поступательное, вращательное вокруг неподвижной оси, вращательное вокруг неподвижной точки и другие. Первые два движения (поступательное и вращательное вокруг неподвижной оси) являются основными движениями твердого тела. Все остальные виды движения, оказывается, можно свести к одному из основных (простейших) движений или к их совокупности. Поэтому рассмотрим именно эти виды движений.

2.2.1. Поступательное движение твердого тела и его кинематические характеристики

Рис. 2.9

Поступательным движением твердого тела называется такое его движение, при котором любая прямая, жестко связанная с телом (например, прямая AB на рис. 2.9), перемещается, оставаясь параллельной самой себе (прямой A₀B₀ в первоначальном положении).

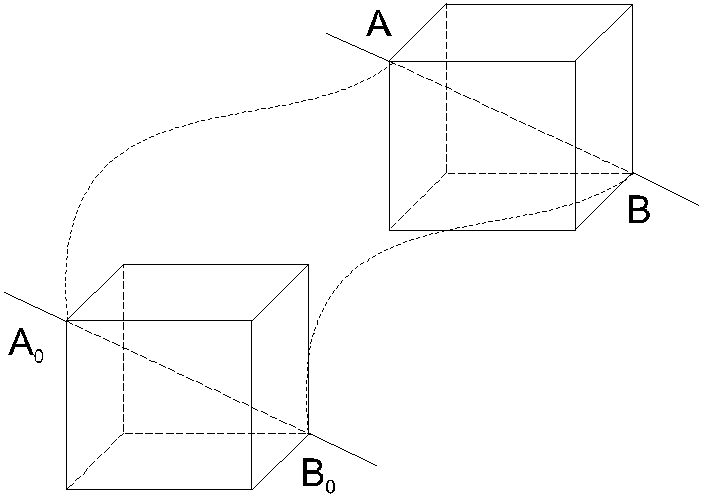
При поступательном движении твердого тела все его точки перемещаются совершенно одинаково: за малое время dt радиус-векторы этих точек изменяются на одну и ту же величину . Соответственно в каждый момент времени скорости всех точек тела одинаковы и равны , а следовательно, одинаковы и их ускорения. Поэтому кинематическое рассмотрение поступательного движения твердого тела сводится к изучению движения любой из его точек. Обычно в качестве такой точки выбирают так называемый центр масс (или центр инерции) тела. Определение этого понятия будет введено ниже, в динамике.

Таким образом, кинематическими характеристиками поступательного движения твердого тела являются уже рассмотренные выше соответствующие характеристики материальной точки.

2.2.2. Вращение твердого тела вокруг неподвижной оси и его кинематические характеристики

Рис. 2.10

Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором все точки тела (например, точка М на рис. 2.10) описывают окружности, центры которых лежат на оси вращения AB, а плоскости окружностей перпендикулярны к ней. Вращение вокруг неподвижной оси совершают, например, роторы турбин, электрических двигателей и т.д.

При вращении, в отличие от поступательного движения, скорости и ускоренияв общем случае у разных точек тела неодинаковы. Поэтому эти характеристики (иногда их называют линейной скоростью и линейным ускорением) не могут служить в качестве кинематических характеристик вращения всего тела в целом.

К основным кинематическим характеристикам вращения твердого тела относятся угол поворота, угловая скорость и угловое ускорение.

Пусть твердое тело вращается вокруг оси , неподвижной в данной системе отсчета. Рассмотрим бесконечно малый поворот тела вокруг этой оси (рис. 2.11).

Положение произвольной точки M этого тела зададим радиус-вектором , проведенным из точкиO неподвижной оси вращения, принимаемой за начало системы координат. Из рисунка следует, что

, (2.39)

где- радиус-вектор, проведенный из центраО окружности, по которой движется точка M; - вектор, проведенный из начала координат в центр окружности О'.

Рис. 2.11

За малое время dt радиус-вектор поворачивается на малый уголd. На такой же угол поворачивается за время dt радиус-вектор любой другой точки тела. Таким образом, угол поворота d характеризует вращение всего твердого тела за малый промежуток времени.

Для того чтобы одновременно задать и угол поворота тела и направление этого поворота, вводят в рассмотрение вектор элементарного (малого) поворота тела, численно равныйd и направленный вдоль оси вращения 00' так, чтобы из его конца поворот тела был виден происходящим против часовой стрелки (рис. 2.11). Начало вектора может находиться в любой точке оси вращения, например в точкеО. Как видно на рис.2.11, направление вектора может быть также определено по правилу правого винта: оно совпадает с направлением поступательного движения правого винта, вращающегося вместе с телом.

Единица угла поворота - радиан (рад).

Для характеристики вращения тела вокруг неподвижной оси вводится угловая скорость.

Угловой скоростью называется векторная величина, характеризующая изменение угла поворота в единицу времени и направление вращения тела вокруг неподвижной оси и равная первой производной от угла поворота по времени, то есть

(2.40)

Из (2.40) следует, что модуль угловой скорости равен

(2.41)

Как следует из (2.40), что направление вектора совпадает с направлением вектора.

Единица угловой скорости - радиан в секунду (рад/с).

Начало вектора также может находиться в любой точке оси вращения, например в точкеО'.

Вращение тела называется равномерным, если модуль угловой скорости не изменяется с течением времени: . В этом случае зависимость угола поворота от времени найдем интегрированием выражения (2.41):

^. (2.42)

Для описания равномерного вращения тела вводятся еще две кинематические характеристики: период вращения и число оборотов в единицу времени.

Периодом вращения называется промежуток времени Т, в течение которого тело, равномерно вращаясь, совершает один полный оборот вокруг оси вращения.

Период вращения выражается в единицах времени, то есть в секундах (с).

Величина n обратная периоду Т, называется числом оборотов в единицу времени, то есть

(2.43)

Очевидно, n измеряется в секундах в минус первой степени (с^-1).

За один полный оборот тело поворачивается на угол 2, поэтому из (2.42) и (2.43) следует, что

^. (2.44)

Для характеристики изменения угловой скорости при неравномерном вращении вводится угловое ускорение.

Угловым ускорением называется векторная величина , характеризующая изменение угловой скорости тела в единицу времени при неравномерном вращении и равная первой производной по времени от его угловой скорости или второй производной по времени от вектора поворота, то есть

(2.45)

Единица углового ускорения - радиан, деленный на секунду в квадрате (рад/с²).

Рис. 2.12

При ускоренном вращении , поэтому векторнаправлен вдоль оси вращения, в ту же сторону, что и. При замедленном вращении, поэтому направление векторапротивоположно направлению вектора(рис 2.12). На этом рисунке- угловая скорость в начальный момент времени, а- в произвольный момент времени.

При равнопеременном вращении . Интегрируя выражение (2.45) для модуля угловой скорости, получим:

^, (2.46)

где - модуль угловой скорости в момент времени принятый за начальный (t=0).

Подставим (2.46) в формулу (2.41) и проинтегрируем, тогда для модуля угла поворота получим выражение

(2.47)