13.2. Намагничивание вещества. Вектор намагниченности

Количественной характеристикой намагничивания магнетиков служит вектор намагниченности, определяемый, как магнитный момент единицы объема магнетика:

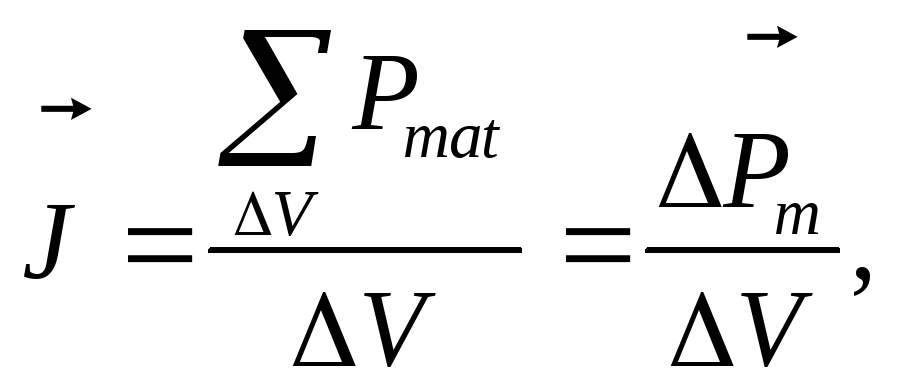(13.3)

где  векторная сумма магнитных моментов отдельных атомов (молекул) в малом объеме V магнетика.

В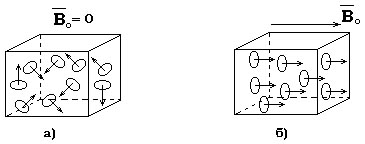отсутствие внешнего магнитного поля () магнетик обычно не намагничен, то есть для него= 0. В диамагнитных веществах это обусловлено равенством нулю результирующего магнитного момента у каждого атома. В парамагнитных телах вследствие хаотичности теплового движения, магнитные моменты отдельных атомов (молекул) ориентированы беспорядочно, поэтому, в отсутствие поляи вектор намагниченности оказывается равным нулю в среднем для не слишком малых объемовV (рис. 13.1, а).

Рис. 13.1

Поместим магнетик в однородное внешнее магнитное поле с индукцией . Под действием этого поля элементарные токи магнетика сориентируются. Магнетик намагнитится и приобретет в расчете на единицу объема магнитный момент(рис. 13.1, б). Ориентированные моменты атомов создают собственное магнитное поле магнетика с индукцией .

Найдем связь между и . Для этого рассмотрим в намагниченном веществе малый элемент объема V=(Sl) в форме тонкого цилиндра, ось которого параллельна направлению вектора намагниченности .

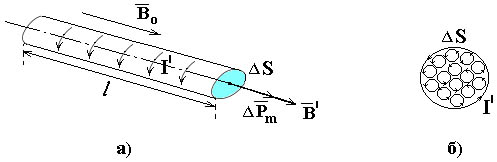
Рис. 13.2

Магнитные моменты микротоков будут ориентированы вдоль оси стержня, а их плоскости – перпендикулярны оси (см. рис. 13.2, а). В любом перпендикулярном оси сечении S cтержня соседние токи на внутренних участках компенсируют друг друга. Нескомпенсированными будут лишь отрезки токов, примыкающие к поверхности магнетика (рис. 13.2, б). Поэтому действие всех микротоков эквивалентно действию сплошного поверхностного микротока I , обтекающего намагниченный стержень.

Магнитный момент этого тока численно равен

Р_m = I   S.

Магнитный момент цилиндра (как совокупность магнитных моментов атомов) выразим из формулы (13.3)

Р_m =J  V =J  Sl.

Приравнивая эти выражения, получим условие эквивалентности магнитных действий микротока и атомов цилиндра:

I = Jl. (13.4)

Теперь собственное поле магнетика с индукцией  можно рассматривать как поле, созданное током I. Цилиндр, обтекаемый этим током, можно представить как тонкий соленоид с одним витком и применить к нему формулу (12.32) при N=1:

Подставляя I из (13.4) с учетом векторного характера величин, получим:

. (13.5)

Таким образом, индукция собственного поля внутри магнетика пропорциональна вектору намагниченности.

3. Поле в магнетиках. Напряженность магнитного поля

Согласно принципу суперпозиции результирующее поле , действующее в намагниченном магнетике, равно

= +, (13.6)

где - индукция (намагничивающего) поля,

- индукция собственного поля.

С учетом формулы (13.5) получим:

(13.7)

Чтобы рассчитать поле , надо знать (или ), которое, в свою очередь, зависит от. Можно избежать этого противоречия и облегчить расчет магнитных полей в веществе, если ввестивспомогательную векторную характеристику - напряженность магнитного поля :

(13.8)

В вакууме микротоки отсутствуют, и вектор намагниченности тождественно равен нулю:

поэтому, согласно (13.8), напряженность магнитного поля для вакуума равна

(13.9)

Подставив (13.7) в (13.8), получим:

Таким образом

(13.10)

Это означает, что напряженность магнитного поля в веществе совпадает с напряженностью внешнего магнитного поля (поля в вакууме)₀. Т.е., вектор зависит только от внешних (макроскопических) токов. В теории магнетизмаиграет такую же роль, как вектор смещенияв теории электричества. (Соответственно, вектор индукциипо своей роли для магнитных полей подобен вектору электрической напряженностив теории электрического поля).

Формула (13.8) показывает, что в системе СИ напряженность магнитного поля, как и вектор намагниченности, имеет размерность. (В системе СГС единицей измеренияявляетсяэрстед (э): 1э = 79,6).