12.5.1 Магнитное поле кругового тока

Определим индукцию магнитного поля в некоторой точке А, лежащей на оси кольцевого (кругового) тока радиуса R на некотором расстоянии L от его центра.

Р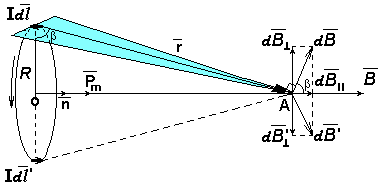азобьем круговой ток на элементы. Каждый элемент создает в точкеА магнитное поле, вектор индукции которого направлен перпендикулярно плоскости, содержащей векторыи(рис. 12.9).

В соответствии с формулой (12.10), поскольку перпендикулярно, аsin = 1 , можно записать:

Разложим вектор на две составляющие: параллельную оси кольца (dВ_II) и перпендикулярную ей (). Составляющая вдоль оси кольца равна

(12.16)

Перпендикулярные оси составляющие иdB^_, созданные диаметрально противоположными элементами и, равны по величине и противоположны по направлению, поэтому уничтожают друг друга. Следовательно, результирующее поле , направлено вдоль оси витка. Его можно найти, проинтегрировав (12.16) по всем элементам кольца с учетом, чтоr=const:

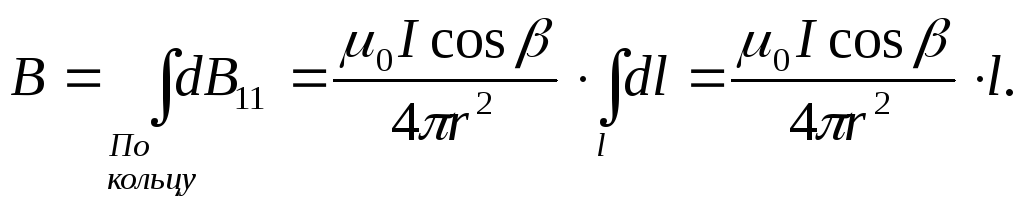
Подставив значение и длины кольца, получим

(12.17)

где

Магнитную индукцию в центре витка (L=0) можно найти, положив в формуле (12.17) r = R:

(12.18)

Умножим числитель и знаменатель формулы (12.17) на  и учтем, что R²=S (площадь витка). Теперь формула (12.17) примет вид

(12.19)

где - магнитный момент витка с током.

Можно показать, что в произвольной точке М поле плоского контура любой формы на большом расстоянии r от него определяется выражением, аналогичным формуле ( ) для электрического поля элементарного диполя:

(12.20)

где  - угол между и . При = 0 формула (12.20) переходит в (12.19).

На рисунке 12.10 изображено поле кругового тока в плоскости листа.

12.5.2. Магнитное поле прямого тока

Найдем индукцию магнитного поля, создаваемого прямым током в точке А, удаленной на расстояние r₀ от оси провода (рис. 12.11). Поля , создаваемые различными элементами тока в этой точке, направлены одинаково (перпендикулярно плоскости, содержащей элемент тока и радиус-вектор ). Таким образом, при расчете индукции поля можно заменить сложение векторов , сложением их модулей. Воспользуемся формулой (12.10), сделав следующие подстановки (рис. 12.11):

Рис. 12.11

В результате, получим следующее выражение:

Если провод имеет конечную длину l, то создаваемое им поле В получим, проинтегрировав последнее выражение в пределах от ₁ до ₂:

(12.21)

Если точка А расположена симметрично относительно концов отрезка, то есть (cos₁ = - cos₂) , то формула (12.21) примет вид

Если провод бесконечно длинный, т.е. длина провода во много раз больше расстояния r₀ до рассматриваемой точки поля (l  r₀), то cos ₁ = 1, поэтому

(12.22)

12.6. Теорема о циркуляции вектора магнитной индукции. Вихревой характер магнитного поля

Магнитное поле может быть охарактеризовано неким общим соотношением, имеющим большое прикладное значение при расчете магнитных полей.

Пусть магнитное поле создано бесконечно длинным прямолинейным проводником с током. Окружим проводник произвольным замкнутым контуром L, плоскость которого перпендикулярна к току (рис. 12.12). В каждой точке контура вектор направлен по касательной к силовой линии (пунктир), проходящей через эту точку. Вычислим циркуляцию вектора магнитной индукциивдоль этого контура, выбрав направление обхода, например, по часовой стрелке.

По определению циркуляция равна интегралу

(12.23)

Подинтегральное выражение  скалярное произведение векторов и можно представить в виде:

(12.24)

где dl_В - проекция отрезка контура dl на направление вектора (рис. 12.12).

Для малого угла d величина dl_В равна

dl_В = rd, (12.25)

где d - угол, на который поворачивается радиус вектор при перемещении вдоль контура наdl ;

r - расстояние от оси тока до начала отрезка dl.

Индукция поля прямого длинного тока на расстоянии r от него определяется формулой (12.22), поэтому

(12.26)

С учетом (12.25) и (12.26) выражения (12.24) и (12.23) примут вид, соответственно:

и (12.27)

При обходе по контуру L, охватывающему ток I, радиус-вектор все время поворачивается в одном направлении, поэтому. Если ток не охватывается контуром, то. Таким образом, выражение (12.27) для циркуляции можно записать:

(12.28)

Доказано, что формула (12.28) справедлива не только для бесконечного прямолинейного тока, но и для полей, источниками которых являются токи произвольной формы.

Рис. 12.13

Если контур L охватывает N токов (рис.12.13), то в любой точке контура индукция результирующего поля определяется по принципу суперпозиции (12.14):

В этом случае циркуляция равна

= (12.29)

где - индукция поля одного проводника.

Заменяя подинтегральное выражение в (12.29) с помощью (12.28), получим

(12.30)

При вычислении суммы (12.30) нужно учитывать знаки токов: положительными считаются те токи, направление которых связано с направлением обхода контура правилом правого винта, отрицательными–токи противоположного направления. Для контура рис. 12.13:

Соотношение (12.30) – это математическое выражение теоремы о циркуляции вектора :

Циркуляция вектора магнитной индукции по произвольному замкнутому контуру L равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром (или пронизывающих поверхность S, опирающуюся на контур).

Если контур L находится в проводящей среде с непрерывным распределением электрического тока, то в соответствии с формулой ( ) сила тока через площадь контура равна

где - вектор плотности тока.

Подставив в (12.28), получим

(12.31)

Воспользуемся теоремой Стокса:

(12.32)

Преобразовав правую часть выражения (12.31) с помощью (12.32) в интеграл по поверхности, получим равенство, которое должно выполняться при произвольном выборе поверхности S:

(12.33)

Это возможно лишь в том случае, если подинтегральные функции в (12.33) будут равны в каждой точке, то есть

(12.34)

Таким образом, мы пришли к дифференциальной форме формулы (12.31): ротор вектора магнитной индукции пропорционален вектору плотности тока в данной точке.

Поля, обладающие отличной от нуля циркуляцией (или ротором) называются вихревыми или соленоидальными.

Ротор вектора можно представить в дифференциальной форме в виде определителя:

= =.

Здесь ,,- орты координатных осей x, у, z,

-оператор «набла».

Модуль вектора rot характеризует степень «завихренности» магнитного поля. Направлен этот вектор по нормали к плоскости, в которой имеет место максимальная «завихренность» (при наблюдении с конца вектора «завихренность» направлена против часовой стрелки).

Формулы (12.30), (12.31) и (12.34) справедливы только для поля в вакууме в отсутствие переменных во времени электрических полей. Физический смысл теоремы о циркуляции вектора магнитной индукции состоит в том, что она выражает закон создания вихревого магнитного поля действием электрических токов. Теорема о циркуляции вектора позволяет находить магнитные поля токов без применения закона Био-Савара-Лапласа. Рассмотрим два примера (см. 12.7.1 и 12.7.2).