Таким образом, линии вектора плотности тока смещения между пластинами непрерывно переходят в линии плотности тока проводимости внутри проводящей пластины.

Согласно гипотезе Максвелла, ток смещения создает в окружающем его пространстве такое же магнитное поле, как и магнитное поле эквивалентного тока проводимости.

Эта гипотеза подтверждена многочисленными проверками вытекающих из нее следствий.

Необходимо отметить, что ток смещения эквивалентен току проводимости только в отношении способности создавать магнитное поле. В отличие от тока проводимости, например, ток смещения не сопровождается выделением ленц-джоулева тепла.

Наряду с током смещения Максвелл ввел понятие полного тока, плотность которого определяется векторной суммой

. (17.8)

Полный ток всегда замкнут. Он имеет одинаковую максимальную величину во всех участках цепи, содержащей как проводники, так и диэлектрики. Если в проводнике создан переменный ток, то внутри него существует переменное электрическое поле, приводящее свободные заряды в движение (ток проводимости) и вызывающее возникновение тока смещения. Значения токов проводимости и токов смещения в металлах и диэлектриках различны, но полный ток (17.8) в них одинаков. Оценим плотности токов проводимости и смещения в металле и диэлектрике. Пусть источник переменной Э.Д.С. создает внутри проводника электрическое поле

,

тогда плотность тока проводимости согласно закону Ома равна

.

Плотность тока смещения в проводнике

.

Отношение максимальных значений плотностей токов

Из этого соотношения нетрудно получить, что для металлического проводника с удельной электропроводностью ~ 10⁸ Сим/м и , плотность тока смещения вплоть до частот оптического диапазона (10¹⁵ Гц). Аналогичный расчет для диэлектрика с удельной электропроводностью ~ 10^-11 Сим/м (кварц) показывает, что плотность тока смещения значительно больше плотности тока проводимости практически для всех частот.

17.4. Второе уравнение Максвелла

Найдем с помощью выражения (17.8) полный ток: через поверхность S, опирающуюся на контур L.

. (17.9)

Во втором интеграле введен знак частотной производной так как вектор изменяется только во времени.

Подставим выражение для полного тока (17.9) в закон полного тока (17.3), тогда получим

. (17.10)

Таким образом закон полного тока формулируется следующим образом: циркуляция вектора напряженности магнитного поля по любому замкнутому контуру равна сумме токов проводимости и смещения, охватываемых этим контуром.

Максвелл и в это уравнение вложил другой смысл: всякое изменение электрического поля сквозь произвольно выбранный воображаемый контур (например, контура L₁, L₂ на рис. 17.2), или ток, текущий в проводнике, создает вихревое магнитное поле.

Уравнение (17.10) называют вторым уравнением Максвелла в интегральной форме.

В вакууме, где отсутствуют свободные заряды и токи , уравнение (17.10) упрощается

(17.11)

Согласно этому уравнению, изменяющееся со временем электрическое поле сквозь любую произвольную воображаемую поверхность, нормальную к полю, создает вихревое магнитное поле, силовые линии которого образуют с направлением вектора правовинтовую систему (рис. 17.4).

Совокупность первого и вто-рого уравнений Максвелла (17.2) и (17.11) характеризует взаимосвязь и взаимозависимость изменений элек-трического и магнитного полей.

В соответствии с (17.11) из-менение во времени электрического смещения в вакууме порождает вихревое магнитное поле, измене-ние которого в соответствии с (17.2) порождает вихревое электрическое поле (рис. 17.5).

В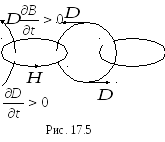следствие этого перемен-ныеэлектрические и магнитные поля могут существовать, вза-имно порождая друг друга и образуя при этом единый электромагнитный процесс, который для своего поддержания не нуждается в электрических токах и представляет собой электромаг-нитные поле в свободном пространстве. Необходимо отме-тить, что первопричиной изме-нения электрического и магнитного полей является все же источники электромагнитного поля – заряды и токи.