13.9.2. Природа парамагнетизма.

В отличие от диамагнетиков, атомы (молекулы) парамагнетиков обладают собственными магнитными моментами (например, любой атом с нечетным числом электронов). В отсутствие внешнего магнитного поля парамагнетик не намагничен (), поскольку из-за теплового движения (Т 0) магнитные моменты атомов ориентированы беспорядочно.

Процесс намагничивания парамагнетика во внешнем магнитном поле состоит в упорядочении расположения магнитных моментов его атомов (или молекул) по отношению к направлению поля : магнитные моменты его атомов начинают прецессировать вокруг направленияс некоторой угловой скоростью (прецессия Лармора). В то же время хаотическое тепловое движение будет их разориентировать. В результате совместного действия этих двух факторов установится некоторая преимущественная ориентация магнитных моментов атомов вдоль поля, причем тем большая, чем больше поле, и тем меньшая, чем выше температура Т.

Проекция магнитного момента некоторого атома на направление поля (рис. 13.9) в некоторый момент времени равна

.

Эта величина различна для разных атомов, и у каждого атома непрерывно меняется со временем. Ее среднее значение равно

= cos. (13.39)

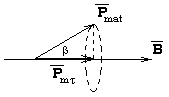
Рис. 13.9

Как показал П. Ланжевен (1905 г.), при наличии магнитного поля среднее значение cos зависит от отношения потенциальной энергии атома в магнитном поле к кинетической энергии его теплового движения. Если магнитное поле не очень сильное, а температура не очень низкая, то есть ВР_mat kT , то

cos =, (13.40)

где k - постоянная Больцмана.

Если парамагнетик однородный и изотропный, то его намагниченность пропорцианальна концентрации n его атомов, т.е.

,

поэтому, учитывая формулы (13.39) и (13.40), получим

cos=. (13.41)

Вектор направлен по направлению поля (парамагнетик намагничивается “по полю”). Это подтверждается экспериментально: при внесении парамагнитного стержня в неоднородное магнитное поле он устанавливается вдоль линий индукции этого поля и втягивается в область более сильного поля.

Разделив (13.41) на Н и положив (так как практическидля парамагнетика), получим восприимчивость:

(13.42)

Согласно (13.42) величина для парамагнетиков не зависит от величины поля (в слабых полях) и обратно пропорциональна термодинамической температуреТ парамагнетика:

(13.43)

где С = и зависит от рода вещества.

Соотношение (13.43) выражает экспериментально установленный закон Кюри, который в теории Ланжевена получил теоретическое объяснение.

В очень сильных полях и при низких температурах может наступить состояние магнитного насыщения, при котором магнитные моменты всех атомов устанавливаются точно по полю, и дальнейшее увеличение поля не приводит к росту намагниченности.

13.9.3. Ферромагнетизм

Ферромагнетиками называются твердые вещества, обладающие (при не слишком высоких температурах) спонтанной намагниченностью, которая сильно изменяется под влиянием внешних воздействий - магнитного поля, деформации, изменения температуры.

Свое название ферромагнетики получили от своего основного представителя - железа (лат. ferrum). Кроме железа, к числу ферромагнетиков относятся никель, кобальт, гадолиний (при t 16⁰С), их сплавы и химические соединения, а также некоторые сплавы и соединения хрома и марганца с другими элементами.

В отличие от слабомагнитных диа - и парамагнетиков ферромагнетики являются сильномагнитными веществами: их внутреннее магнитное поле () может в сотни и тысячи раз превосходить внешнее поле ().

Помимо способности сильно намагничиваться, ферромагнетики обладают еще целым рядом свойств.

1. Характерной особенностью ферромагнетиков является сложная нелинейная зависимость между индукциейВ и напряженностью Н поля. Эта зависимость была установлена в работах А.Г. Столетова на примере мягкого (отожженного) железа. Зависимости В от Н для некоторых ферромагнетиков приведены на рис. 13.10, а.

Индукция сначала быстро увеличивается, но по мере намагничивания магнетика ее нарастание замедляется. По значениям В и Н можно найти намагниченность

Зависимость J от Н (кривая намагничивания) изображена на рис. 13.10, б. Уже при напряженности поля Н 100 намагниченность достигает максимального значенияJ_S (насыщение) и практически перестает зависеть от Н.

Вследствие нелинейной зависимостиВ от Н (J от Н) магнитная проницаемость ферромагнетика и его магнитная восприимчивостьзависят от напряженности магнитного поля. График зависимостииотН дан на рис. 13.11. Максимальное значение _m достигается несколько раньше, чем насыщение.

Поскольку то при неограниченном возрастанииН магнитная проницаемость асимптотически приближается к единице, т.к. при J J_S=const, J_S /Н 0.

2. Если ферромагнетик представляет собой единый монокристалл, то вид кривой намагничивания зависит от направления намагничивающего поля относительно осей кристалла (рис. 13.12). Это свойство называется - анизотропия. Для каждого ферромагнетика существует направление легкого (кривая 1), среднего (кривая 2) и трудного намагничивания (кривая 3).

Рис. 13.12

Эти направления для элементарной кристаллической ячейки железа показаны на том же рисунке. Если ферромагнетик имеет мелкокристаллическую структуру (поликристалл), то анизотропия намагничивания не проявляется.

2. Для ферромагнетиков характерно наличиегистерезиса. Это явление состоит в том, что величина J в ферромагнетике определяется не только значением напряженности поля Н в данный момент, но зависит от предыдущих состояний намагничивания (от предистории), причем происходит своеобразное отставание изменения J (или В) от изменений Н. Так, если намагнитить ферромагнетик до насыщения (точка 1 на рис. 13.13), а затем начать уменьшать напряженность Н намагничивающего поля, то, как показывает опыт, уменьшение намагниченности J будет происходить согласно кривой (1-2), лежащей выше кривой намагничивания (0-1).

Рис. 13.13

В результате, когда внешнее поле уменьшится до нуля (точка 2), намагниченность не исчезает: J = J_r  остаточная намагниченность.

Намагниченность обращается в ноль лишь под действием поля Н =Н_с (точка 3 на рис. 13.13) противоположного направления (Н_с – коэрцитивная сила). С наличием остаточной намагниченности связано существование постоянных магнитов, которые тем лучше сохраняют свои свойства, чем больше коэрцитивная сила ферромагнитного материала.

П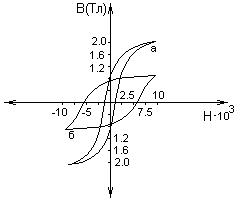ри действии на ферромагнетик переменного магнитного поля намагниченность изменяется циклически в соответствии с кривой 1-2-3-4-5-6-1 (рис. 13.13), которая называетсяпетлей гистерезиса (сплошная кривая - максимальная петля – намагничивание достигает насыщения; пунктирная кривая – один из частных циклов). Величины J_r (или В_r), Н_c и зависят от условий получения данного магнитного материала и его обработки и являются основными характеристиками ферромагнетика, определяющими его применимость для тех или иных целей. Так, еслиН_c велика (магнито - жесткий материал с широкой петлей гистерезиса – рис. 13.14, кривая 1), то ферромагнетик используют, например, для изготовления постоянных магнитов. Если Н_с мала (магнито-мягкий материал с узкой петлей - рис.13.14, кривая 2), то потери энергии при перемагничевании будут малы. Такие ферромагнетики применяют для изготовления сердечников электромагнитов, трансформаторов, генераторов, двигателей и т.д.

Рис. 13.14

В таблице 13.1. приведены характеристики некоторых ферромагнетиков.

Таблица 13.1

Магнито-мягкие			Магнито-жесткие
Материал и его состав	m	Нс, А/м	Материал и его состав	Нс, А/м	Вr, Тл
Железо (99,9% Fе)	5 103	80	Альнико 53%-Fe 18%-Co 10%-Al 19%-Ni	52 103	0,9
Кремниевое Железо (Fe-Si) (96,7% – Fe; 3,3% - Si)	5104	16	Магнико 50%-Fe 24%-Co 13,5%-Ni 9%-Al 3%-Cu	56 103	1,3
Отожженное в потоке водорода Супермаллой (Ni –Fe – Mo) 79% Ni; 16% Fe; 5% Мо	4104 8105	8	77%-Pt 23%-Со	21 104	0,45

Обнаружено, что некоторые сплавы из неферромагнитных элементов (при определенном процентном отношении между компонентами) обладают сильным ферромагнетизмом, например:

Mn – Bi ; Mn – Sb; Cr – Те и другие.

4. Магнитные и другие физические свойства ферромагнетиков обладают специфической зависимостью от температуры. Так, при увеличении температуры намагниченность насыщения монотонно уменьшается (рис. 13.15), обращаясь в ноль при температуреТ_к (точка Кюри).

Рис. 13.15

В таком состоянии магнитная восприимчивость ферромагнетика подчиняется закону Кюри – Вейса:

где С – постоянная, зависящая от рода вещества. При нагревании выше температуры Т_к ферромагнетик не только теряет свои ферромагнитные свойства, но у него изменяется теплоемкость, электропроводность и некоторые другие характеристики. Точка Кюри у железа – 1043 К, у кобальта – 1403 К, у никеля – 631 К.

5. Процесс намагничивания ферромагнетика сопровождается изменением его линейных размеров и объема. Это явление получило название магнитострикция (открыта Д. Джоулем в 1842г.). Величина и знак эффекта зависят от величины магнитного поля, природы ферромагнетика, направления намагничивания.

Существует и обратный магнитомеханический эффект, состоящий в изменении намагниченности ферромагнитного образца при его механической деформации (эффект Виллари, 1865г.). Эти явления применяются в магнитострикционных датчиках и реле. Механические колебания, возникающие в ферромагнетиках при их намагничивании в переменном магнитном поле, используют в магнитострикционных излучателях ультразвука.