
- •Глава III. Магнетизм
- •§12. Магнитное поле в вакууме
- •12.1. Опыт Эрстеда. Индукция магнитного поля
- •Магнитное поле
- •12.2. Поток вектора . Теорема Гаусса
- •12.3 Магнитное взаимодействие токов. Закон Ампера
- •Закон Био-Савара-Лапласа
- •12.5 Принцип суперпозиции. Применение закона
- •12.5.1 Магнитное поле кругового тока
- •12.5.2. Магнитное поле прямого тока
- •12.6. Теорема о циркуляции вектора магнитной индукции. Вихревой характер магнитного поля
- •12.7. Магнитное поле соленоида
- •12.7. 1. Магнитное поле тороида
- •§13. Магнитное поле в веществе
- •Электрона и атома
- •13.2. Намагничивание вещества. Вектор намагниченности
- •Поле в магнетиках. Напряженность магнитного поля
- •13.4. Магнитная восприимчивость и магнитная проницаемость
- •13.5. Теорема о циркуляции вектора
- •13.6. Расчет магнитного поля длинного стержневого проводника с током
- •Граничные условия для векторов и
- •13.8. Расчет магнитного поля в неоднородных средах
- •Типы магнетиков
- •13.9.1. Природа диамагнетизма
- •13.9.2. Природа парамагнетизма.
- •13.9.3. Ферромагнетизм
- •13.9.4. Природа ферромагнетизма
- •§ 14. Заряды и токи в магнитном поле
- •14.1. Сила Ампера и сила Лоренца
- •Силу (14.4) называют силой Лоренца. Ее величина
- •14.2. Закономерности движения заряженных частиц в магнитном поле
- •14.3. Ускорители заряженных частиц
- •Внутри дуанта электрическое поле отсутствует, поэтому
- •Контур с током в магнитном поле
- •В неоднородном магнитном поле помимо вращательного момента, стремящегося повернуть виток, будет действовать сила, вызывающая поступательное перемещение витка с током.
- •Если в процессе перемещения сила тока не меняется, то
- •14.5. Физические принципы работы электроизмерительных приборов
- •14.5.1. Магнитоэлектрическая система
- •Таким образом,
- •14.5.2. Электродинамическая система
- •§15. Электромагнитная индукция
- •Явление электромагнитной индукции. Закон Фарадея. Правило Ленца
- •Если потоки, пронизывающие витки, одинаковы, то
- •15.2. Генераторы и электродвигатели
- •15.2.1. Генератор переменного тока
- •15.2.2. Генератор постоянного тока и электродвигатель
- •Токи Фуко
- •15.4. Явление самоиндукции. Индуктивность
- •Потокосцепление самоиндукции такого соленоида
- •15.5. Токи при размыкании и замыкании цепи
- •15.6. Природа э.Д.С. Индукции
- •15.7. Явление взаимной индукци
- •15.8. Физические принципы работы трансформатора
- •§ 16.Энергия магнитного поля
- •16.1. Магнитная энергия контуров с током
- •16.2. Энергия магнитного поля. Плотность магнитной энергии
- •§ 17. Обобщение законов электромагнетизма. Уравнения Максвелла
- •17.1. Обобщение закона электромагнитной индукции. Первое уравнение Максвелла
- •17.2 Обобщение теоремы о циркуляции вектора напряженности магнитного поля. Ток смещения
- •17.3 Вектор плотности тока смещения
- •Таким образом, линии вектора плотности тока смещения между пластинами непрерывно переходят в линии плотности тока проводимости внутри проводящей пластины.
- •17.4. Второе уравнение Максвелла
- •17.5. Система уравнений Максвелла
13.9.1. Природа диамагнетизма
Диамагнетизм, как свойство вещества намагничиваться навстречу направлению действующего на него внешнего магнитного поля, свойственен всем веществам.
При
внесении тела в магнитное поле в
электронной оболочке каждого его атома
возникают индуцированные круговые токи
I,
т.е. добавочное круговое движение
электронов. Эти токи создают в каждом
атоме индуцированный
магнитный момент
![]() ,
направленный, согласно правилу Ленца
(§ 15.1) противоположно внешнему магнитному
полю (независимо от того, имелся ли у
атома собственный магнитный момент
,
направленный, согласно правилу Ленца
(§ 15.1) противоположно внешнему магнитному
полю (независимо от того, имелся ли у
атома собственный магнитный момент
![]() или нет (см. формулу (13.1)) и как он был
ориентирован.
или нет (см. формулу (13.1)) и как он был
ориентирован.
У ряда веществ слабый диамагнитный эффект “маскируется” другими более сильными эффектами.
В
изолированных атомах токи, создающие
диамагнетизм, имеют простой характер.
Рассмотрим его более подробно. При
внесении атома в магнитное поле, орбита
каждого из его электронов начинает
вращаться вокруг направления вектора
индукции
![]() поля (прецессировать), при этом вектор
поля (прецессировать), при этом вектор![]() орбитального магнитного момента
отдельного (i-ого)
электрона описывает конус (подобно
движению оси волчка в поле сил тяжести).
орбитального магнитного момента
отдельного (i-ого)
электрона описывает конус (подобно
движению оси волчка в поле сил тяжести).
Таким
образом, вся
совокупность электронов атома приобретает
под действием внешнего магнитного поля
![]() синхронное вращательное движение
вокруг оси, проходящей через центр атома
параллельно
синхронное вращательное движение
вокруг оси, проходящей через центр атома
параллельно![]() .
Это вращение
электронов атома называется прецессией
Лармора (или
ларморовой прецессией). Она происходит
с одинаковой для всех электронов угловой
скоростью
.
Это вращение
электронов атома называется прецессией
Лармора (или
ларморовой прецессией). Она происходит
с одинаковой для всех электронов угловой
скоростью
![]() - частотой ларморовой прецессии
- частотой ларморовой прецессии
![]() =
=![]() , (13.33)
, (13.33)
где е - заряд электрона,
me -его масса.
L 10-13с-1.
Дополнительное
вращение каждого электрона происходит
как бы по окружности радиуса
![]() .
Направлению этого вращения, противоположному
движению электрона по орбите, соответствует
наведенный индуцированный круговой
ток
.
Направлению этого вращения, противоположному
движению электрона по орбите, соответствует
наведенный индуцированный круговой
ток![]() с магнитным моментом, направленным
противоположно
с магнитным моментом, направленным
противоположно![]() (рис. 13.8):
(рис. 13.8):
![]() (13.34)
(13.34)
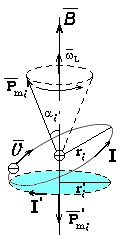
Поскольку
каждый электрон движется по прецессирующей
орбите, расстояние
![]() все время меняется, поэтому в формуле
(13.34) нужно брать усредненное по времени
расстояние(
все время меняется, поэтому в формуле
(13.34) нужно брать усредненное по времени
расстояние(![]() )2,
которое зависит от ориентации плоскости
орбиты относительно
)2,
которое зависит от ориентации плоскости
орбиты относительно
![]() ,
т.е. от угла
,
т.е. от угла![]() .
Если провести усреднение по всем
возможным значениям угла
.
Если провести усреднение по всем
возможным значениям угла![]() ,
считая их равновероятными, и учесть
вытянутость орбиты, то получим
,
считая их равновероятными, и учесть
вытянутость орбиты, то получим
Рис. 13.8
(![]() )2
=
)2
=![]()
![]()
, (13.35)
, (13.35)
где
![]()
- среднее значение квадрата расстояния
электрона от ядра атома.
- среднее значение квадрата расстояния
электрона от ядра атома.
Подставив (13.33) в (13.34), получим среднее значение индуцированного магнитного момента отдельного электрона:
![]()
![]() =
=![]()
![]()
![]() .
(13.36)
.
(13.36)
Поскольку
![]() и
и
![]() =
=![]() ,
(13.37)
,
(13.37)
то, подставив (13.33) и (13.37) в (13.36) и просуммировав по всем электронам атома, найдем индуцированный магнитный момент многоэлектронного атома:
![]()
![]() =
=
![]()
![]()
![]() ,
(13.38)
,
(13.38)
где Z - число электронов в атоме (атомный номер химического элемента).
Знак
“минус” в формуле (13.38) отражает тот
факт, что векторы ![]()
и
и
![]() направлены в противоположные стороны.
направлены в противоположные стороны.
Можно рассчитать диамагнитную восприимчивость совокупности изолированных атомов (например, одного моля вещества), если известно число электронов в атомах и их пространственное распределение. В случае однородного магнетика с концентрацией атомов n=N/V вектор намагниченности равен
 (т.к.
(т.к.
![]() ).
).
Отсюда, с учетом формулы (13.37), получим удельную магнитную восприимчивость диамагнетика:
![]()
![]() .
.
Последняя формула показывает, что магнитная восприимчивость диамагнетика не зависит от величины намагничивающего поля и температуры, что согласуется с опытными данными.
Если атомы не изолированы друг от друга и взаимодействуют между собой, например, в молекулах или кристаллах, то электронные оболочки в атомах деформируются, и наблюдаемый диамагнетизм оказывается меньше, чем у изолированных атомов.
Однако,
межатомная связь в отдельных случаях,
напротив, приводит к усилению диамагнитного
эффекта. Например, в металлах и
полупроводниках под воздействием
внешнего магнитного поля электроны
проводимости начинают двигаться по
спиральным квантовым орбитам, что также
вызывает появление диамагнитного
эффекта (диамагнетизм Ландау). Он особенно
велик, например, в висмуте (![]() )
и графите. Наибольшее по модулю значение
магнитной восприимчивости (
)
и графите. Наибольшее по модулю значение
магнитной восприимчивости (![]() )
имеют сверхпроводники, внутри которых
)
имеют сверхпроводники, внутри которых![]() ,
а диамагнетизм обусловлен макроскопическими
поверхностными токами.
,
а диамагнетизм обусловлен макроскопическими
поверхностными токами.
