1.4.2. Преобразование эц с различным соединением сопротивлений

1. Последовательным соединением сопротивлений называется такое, когда конец первого сопротивления соединяется с началом второго, конец второго сопротивления с началом третьего и т.д. Начало первого сопротивления и конец последнего подключаются к источнику питания или к каким-либо точкам ЭЦ (рис. 1. 9.). Во всех сопротивлениях протекает один и

Рис. 1.9.

тот же ток.

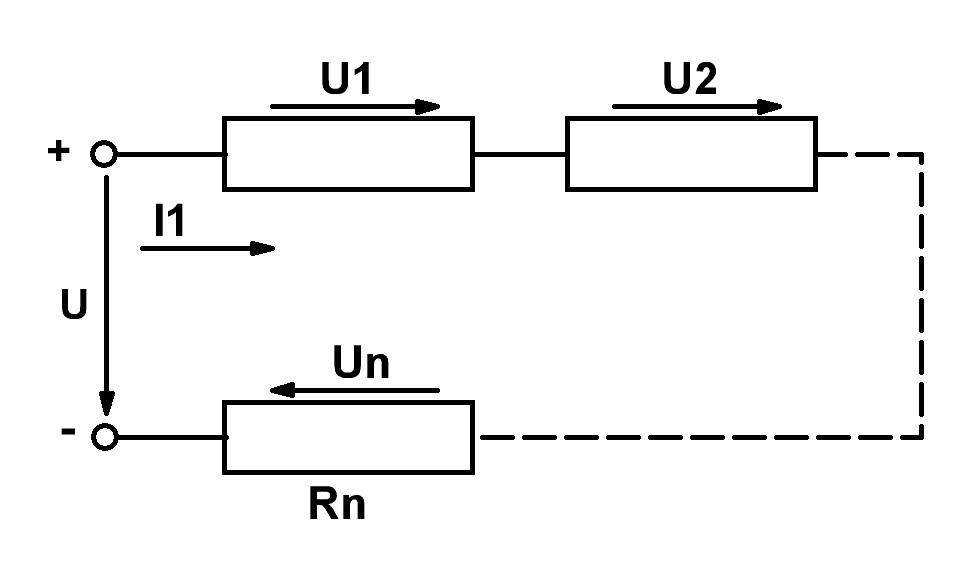
Рис. 1. 9.

Ток в цепи, напряжения на сопротивлениях и потребляемые ими мощности определяются следующими соотношениями.

1. Эквивалентное сопротивление электрической цепи .

2. Ток в сопротивлениях цепи .

3. Напряжение и мощность, подводимые к электрической цепи с последовательным соединением сопротивлений равны, соответственно, сумме напряжений и мощностей ,

.

4. Напряжение и мощности распределяются пропорционально сопротивлениям .

2. При параллельном соединении сопротивлений соединяются между собой как начало всех сопротивлений, так и их концы (рис. 1.10.).

Характерным для параллельного соединения является одно и то же напряжение на зажимах всех сопротивлений. Параллельно соединяются обычно различные приемники электрической энергии, рассчитанные на одно и то же напряжение. При параллельном соединении не требуется согласовывать номинальные данные приемников, возможно включение и отключение любых приемников независимо от остальных, а при выходе из строя любого из них остальные остаются включенными.

а)

б)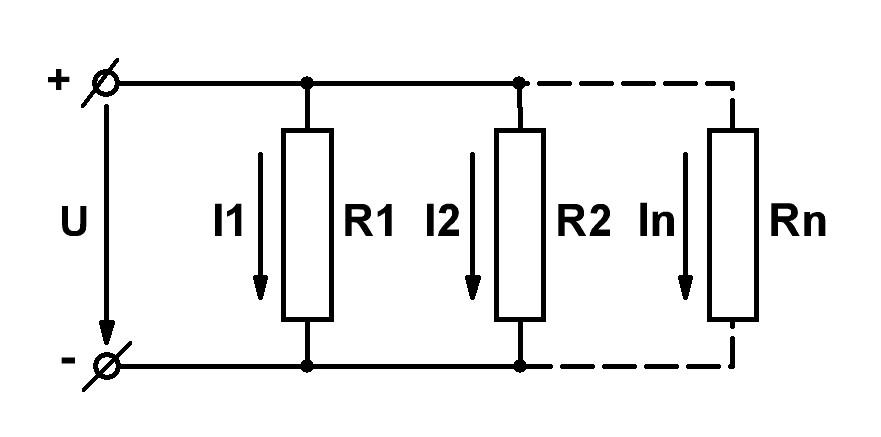

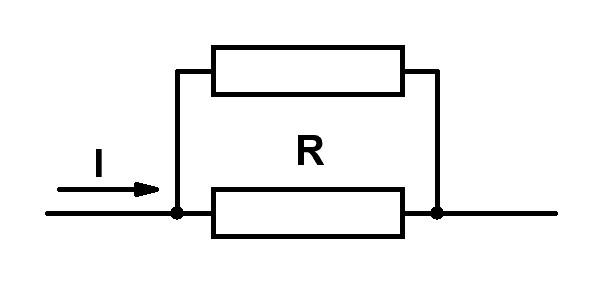
Рис. 1. 10.

Параллельное соединение можно применить, если требуется уменьшить сопротивления какого-либо участка электрической цепи, как показано на рис. 1.10.б).

Токи и мощности параллельно соединенных ветвей рис.1.10.а) при не зависят друг от друга.

1. Общий ток равен сумме токов параллельно соединенных ветвей

,

где: − эквивалентная проводимость, равная

−эквивалентное сопротивление, .

2. Токи и мощности в ветвях в ветвях вычисляются по формулам ;;;.

3. Отношение токов и мощностей равно отношению проводимостей и обратно пропорционально отношению сопротивлений

.

При увеличении параллельно соединенных сопротивлений эквивалентная проводимость ЭЦ увеличивается, а эквивалентное сопротивление уменьшается, что приводит к увеличению тока. Если напряжение остается const, то увеличивается также общая мощность.

, или .

3. Смешанным или последовательно-параллельным называется такое соединение сопротивлений, при котором на одних участках ЭЦ сопротивления соединены параллельно, а на других последовательно.

Анализ и расчет ЭЦ со смешанным соединением сопротивлений производится методом преобразований. Электрическая цепь (рис. 1.11.а) заменяется последовательно эквивалентными цепями до образования схемы, изображенной на рис. 1.11.б).

а)

б)

Рис. 1.11.

В соединении «треугольником» конец одного из сопротивлений соединяется с началом следующего и т.д., а узлы a,b,c подключаются к остальной части ЭЦ. В соединении «звездой» все концы соединяются вместе, а начала фаз подключаются к схеме. Если заменить сопротивление ,,, соединенные в треугольник, эквивалентными сопротивлениями, соединенными звездой, то получим цепи со смешанным соединением сопротивлений.

Преобразование «звезды» в «треугольник»

а)

б)

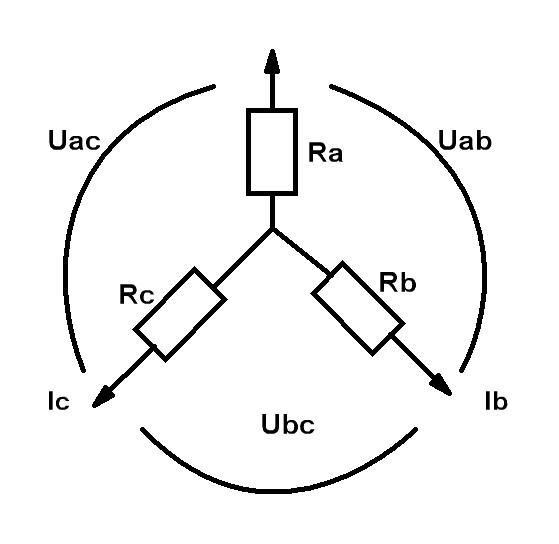
Рис. 1. 12.

После замены токи и направлениядолжны остаться без изменений.

Для «треугольника» ;

Для соединения звездой

По условию эквивалентности эквивалентные сопротивление обеих схем равны , следовательно, можно записать

1. ;

Структуры соединением «треугольник» и «звезда» по отношению к узлам симметричны, поэтому циклично запишем

2. ;

3. .

Сложим 1) и 3), вычтем 2), всё поделим на 2, получим

, ,.

Если в «треугольнике» равны, то и в «звезде» равны:.

Возможно обратное преобразование звезды из резистивных элементов в эквивалентный треугольник. Для этого надо попарно перемножить 1) и 3) и сложить, затем вынести общий множитель и полученное уравнение разделить на 3)уравнение, т.е. . Далее поочередно поделить то же уравнение наи.

Путем циклической подстановки индексов при преобразовании звезды в треугольник получим

, ,.

На рис. 1.13. поясняется упрощение схемы путем последовательной замены эквивалентными цепями при преобразовании «треугольника» в «звезду».

а

)б)

в

Рис. 1.13.

)г)