Data-Structures-And-Algorithms-Alfred-V-Aho

Data Structures and Algorithms: CHAPTER 8: Sorting

2.Use the procedure partition from Fig. 8.13 to divide A[i], . . . , A [j] into two groups: A[i], . . . , A[m - 1] with keys less than v, and A [m], . . . , A [j] with keys v or greater.

3.If k ≤ m - i, so the kth among A [i], . . . , A [j] is in the first group, then call select(i, m - 1, k) . If k > m - i, then call select(m, j, k - m + i).

Eventually we find that select(i, j, k) is called, where all of A[i], . . . , A [j] have the same key (usually because j=i). Then we know the desired key; it is the key of any of these records.

As with quicksort, the function select outlined above can take Ω(n2) time in the worst case. For example, suppose we are looking for the first element, but by bad luck, the pivot is always the highest available key. However, on the average, select is even faster than quicksort; it takes O(n) time. The principle is that while quicksort calls itself twice, select calls itself only once. We could analyze select as we did quicksort, but the mathematics is again complex, and a simple intuitive argument should be convincing. On the average, select calls itself on a subarray half as long as the subarray it was given. Suppose that to be conservative, we say that each call is on an array 9/10 as long as the previous call. Then if T(n) is the time spent by select on an array of length n, we know that for some constant c we have

Using techniques from the next chapter, we can show that the solution to (8.14) is T(n) = O(n).

A Worst-Case Linear Method for Finding Order Statistics

To guarantee that a function like select has worst case, rather than average case, complexity O(n), it suffices to show that in linear time we can find some pivot that is guaranteed to be some positive fraction of the way from either end. For example, the

solution to (8.14) shows that if the pivot of n elements is never less than the

element, nor greater than the element, so the recursive call to select is on at most nine-tenths of the array, then this variant of select will be O(n) in the worst

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1208.htm (36 of 44) [1.7.2001 19:22:21]

Data Structures and Algorithms: CHAPTER 8: Sorting

case.

The trick to finding a good pivot is contained in the following two steps.

1.Divide the n elements into groups of 5, leaving aside between 0 and 4

elements that cannot be placed in a group. Sort each group of 5 by any algorithm and take the middle element from each group, a total of ën/5û

elements.

2.Use select to find the median of these ën/5û elements, or if ën/5û is even, an element in a position as close to the middle as possible. Whether ën/5û is even or odd, the desired element is in position .

This pivot is far from the extremes, provided that not too many records have the pivot for key.† To simplify matters let us temporarily assume that all keys are

different. Then we claim the chosen pivot, the element of the middle

elements out of groups of 5 is greater than at least of the n elements. For it exceeds of the middle elements, and each of those exceeds two more, from the five of which it is the middle. If n ³ 75, then is at least n/4. Similarly,

we may check that the chosen pivot is less than or equal to at least

elements, so for n ³ 75, the pivot lies between the 1/4 and 3/4 point in the sorted order. Most importantly, when we use the pivot to partition the n elements, the kth element will be isolated to within a range of at most 3n/4 of the elements. A sketch of the complete algorithm is given in Fig. 8.25; as for the sorting algorithms it assumes an array A[1], . . . , A[n] of recordtype, and that recordtype has a field key of type keytype. The algorithm to find the kth element is just a call to select(1,n,k), of course.

function select ( i, j, k: integer ): keytype;

{returns the key of the kth element in sorted order among A[i], . . . ,A[j] }

var

m: integer; { used as index } begin

(1)if j-i < 74 then begin { too few to use select recursively }

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1208.htm (37 of 44) [1.7.2001 19:22:21]

Data Structures and Algorithms: CHAPTER 8: Sorting

Fig. 8.25. Worst-case linear algorithm for finding kth element.

To analyze the running time of select of Fig. 8.25, let n be j - i + 1. Lines (2) and

(3) are only executed if n is 74 or less. Thus, even though step (2) may take O(n2) steps in general, there is some constant c1, however large, such that for n £ 74, lines (1 - 3) take no more than c1 time.

Now consider lines (4 - 10). Line (7), the partition step, was shown in connection with quicksort to take O(n) time. The loop of lines (4 - 5) is iterated about n/5 times, and each execution of line (5), requiring the sorting of 5 elements, takes some constant time, so the loop takes O(n) time as a whole.

Let T(n) be the time taken by a call to select on n elements. Then line (6) takes at most T(n/5) time. Since n ³ 75 when line (10) is reached, and we have argued that if n ³ 75, at most 3n/4 elements are less than the pivot, and at most 3n/4 are equal to or greater than the pivot, we know that line (9) or (10) takes time at most T(3n/4).

Hence, for some constants c1 and c2 we have

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1208.htm (38 of 44) [1.7.2001 19:22:21]

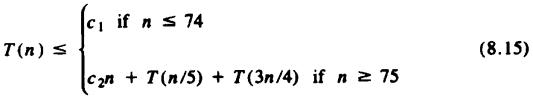
Data Structures and Algorithms: CHAPTER 8: Sorting

The term c2n in (8.15) represents lines (1), (4), (5), and (7); the term T(n/5) comes from line (6), and T(3n/4) represents lines (9) and (10).

We shall show that T(n) in (8.15) is O(n). Before we proceed, the reader should now appreciate that the "magic number" 5, the size of the groups in line (5), and our selection of n = 75 as the breakpoint below which we did not use select recursively, were designed so the arguments n/5 and 3n/4 of T in (8.15) would sum to something less than n. Other choices of these parameters could be made, but observe when we solve (8.15) how the fact that 1/5 + 3/4 < 1 is needed to prove linearity.

Equation (8.15) can be solved by guessing a solution and verifying by induction that it holds for all n. We shall chose a solution of the form cn, for some constant c. If we pick c ³ c1, we know T(n) £ cn for all n between 1 and 74, so consider the case n

³ 75. Assume by induction that T(m) £ cm for m<n. Then by (8.15),

If we pick c = max(c1, 20c2), then by (8.16), we have T(n) £ cn/20 + cn/5 + 3cn/4 = cn, which we needed to show. Thus, T(n) is O(n).

The Case Where Some Equalities Among

Keys Exist

Recall that we assumed no two keys were equal in Fig. 8.25. The reason this assumption was needed is that otherwise line (7) cannot be shown to partition A into blocks of size at most 3n/4. The modification we need to handle key equalities is to add, after step (7), another step like partition, that groups together all records with key equal to the pivot. Say there are p ³ 1 such keys. If m - i £ k £ m - i + p, then no recursion is necessary; simply return A[m].key. Otherwise, line (8) is unchanged, but line (10) calls select(m + p, j, k - (m - i) - p).

Exercises

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1208.htm (39 of 44) [1.7.2001 19:22:21]

Data Structures and Algorithms: CHAPTER 8: Sorting

a.What modifications to the quicksort algorithm of Fig. 8.14 do we have to make to avoid infinite loops when there is a sequence of equal elements?

b.Show that the modified quicksort has average-case running time O(n log n).

8.1

Here are eight integers: 1, 7, 3, 2, 0, 5, 0, 8. Sort them using (a) bubblesort, (b) insertion sort, and (c) selection sort.

Here are sixteen integers: 22, 36, 6, 79, 26, 45, 75, 13, 31, 62, 27, 76, 33,

8.216, 62, 47. Sort them using (a) quicksort, (b) insertion sort, (c) heapsort, and (d) bin sort, treating them as pairs of digits in the range 0-9.

The procedure Shellsort of Fig. 8.26, sometimes called diminishing-

increment sort, sorts an array A[1..n] of integers by sorting n/2 pairs (A[i],A[n/2 + i]) for 1 ≤ i ≤ n/2 in the first pass, n/4 four-tuples (A[i], A[n/4 + i], A[n/2 + i], A[3n/4 + i]) for 1 ≤ i ≤ n/4 in the second pass, n/8

eight-tuples in the third pass, and so on. In each pass the sorting is done using insertion sort in which we stop sorting once we encounter two elements in the proper order.

procedure Shellsort ( var A: array[l..n] of integer );

var

i, j, incr: integer; begin

incr := n div 2;

while incr > 0 do begin

end

end; { Shellsort }

Fig. 8.26. Shellsort.

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1208.htm (40 of 44) [1.7.2001 19:22:21]

Data Structures and Algorithms: CHAPTER 8: Sorting

a.Sort the sequences of integers in Exercises 8.1 and 8.2 using

Shellsort.

b.Show that if A[i] and A[n/2k + i] became sorted in pass k (i.e., they were swapped), then these two elements remain sorted in pass k + 1.

c.The distances between elements compared and swapped in a pass diminish as n/2, n/4, . . . , 2, 1 in Fig. 8.26. Show that Shellsort will work with any sequence of distances as long as the last distance is 1.

d.Show that Shellsort works in O (n1.5) time.

Suppose you are to sort a list L consisting of a sorted list followed by a *8.4 few "random" elements. Which of the sorting methods discussed in this

chapter would be especially suitable for such a task?

*8.5

A sorting algorithm is stable if it preserves the original order of records with equal keys. Which of the sorting methods in this chapter are stable?

*8.6

Suppose we use a variant of quicksort where we always choose as the pivot the first element in the subarray being sorted.

Show that any sorting algorithm that moves elements only one position at

8.7a time must have time complexity at least Ω(n2).

In heapsort the procedure pushdown of Fig. 8.17 establishes the partially ordered tree property in time O(n). Instead of starting at the leaves and

8.8pushing elements down to form a heap, we could start at the root and push elements up. What is the time complexity of this method?

Suppose we have a set of words, i.e., strings of the letters a - z, whose total length is n. Show how to sort these words in O(n) time. Note that if

*8.9 the maximum length of a word is constant, binsort will work. However, you must consider the case where some of the words are very long.

Show that the average-case running time of insertion sort is Ω(n2).

*8.10

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1208.htm (41 of 44) [1.7.2001 19:22:21]

Data Structures and Algorithms: CHAPTER 8: Sorting

Show that any algorithm to purge duplicates from a list requires at least

*8.18

Ω(n log n) time under the decision tree model of computation of Section 8.6.

Suppose we have k sets, S1, S2, . . . , Sk, each containing n real numbers. Write a program to list all sums of the form s1 + s2 + . . . + sk, where si is

*8.19

in Si, in sorted order. What is the time complexity of your program?

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1208.htm (42 of 44) [1.7.2001 19:22:21]

Data Structures and Algorithms: CHAPTER 8: Sorting

Suppose we have a sorted array of strings s1, s2, . . . , sn. Write a program to determine whether a given string x is a member of this sequence. What

*8.20 is the time complexity of your program as a function of n and the length of x?

Bibliographic Notes

Knuth [1973] is a comprehensive reference on sorting methods. Quicksort is due to Hoare [1962] and subsequent improvements to it were published by Singleton [1969] and Frazer and McKellar [1970]. Heapsort was discovered by Williams [1964] and improved by Floyd [1964]. The decision tree complexity of sorting was studied by Ford and Johnson [1959]. The linear selection algorithm in Section 8.7 is from Blum, Floyd, Pratt, Rivest, and Tarjan [1972].

Shellsort is due to Shell [1959] and its performance has been analyzed by Pratt [1979]. See Aho, Hopcroft, and Ullman [1974] for one solution to Exercise 8.9.

† Technically, quicksort is only O(n log n) in the average case; it is O(n2) in the worst case.

‡We could copy A[i], . . . ,A[j] and arrange them as we do so, finally copying the result back into A[i], . . . ,A[j]. We choose not to do so because that approach would waste space and take longer than the in-place arrangement method we use.

†If there is reason to believe nonrandom orders of elements might make quicksort run slower than expected, the quicksort program should permute the elements of the array at random before sorting.

†Since we only want the median, not the entire sorted list of k elements, it may be better to use one of the fast median-finding algorithms of Section 8.7.

†We could at the end, reverse array A, but if we wish A to end up sorted lowest first, then simply apply a DELETEMAX operator in place of DELETEMIN, and partially order A in such a way that a parent has a key no smaller (rather than no larger) than its children.

†In fact, this time is O(n), by a more careful argument. For j in the range n/2 to

n/4+1, (8.8) says only one iteration of pushdown's while-loop is needed. For j

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1208.htm (43 of 44) [1.7.2001 19:22:21]

Data Structures and Algorithms: CHAPTER 8: Sorting

between n/4 and n/8+1, only two iterations, and so on. The total number of iterations

as j ranges between n/2 and 1 is bounded by Note that the improved bound for lines (1 - 2) does not imply an improved bound for heapsort as a whole; all the time is taken in lines (3 - 5).

†Note that a sequence ranging from 1 to 0 (or more generally, from x to y, where y < x) is deemed to be an empty sequence.

†But in this case, if log n-bit integers can fit in one word, we are better off treating keys as consisting of one field only, of type l..n, and using ordinary binsort.

†We may as well assume all keys are different, since if we can sort a collection of distinct keys we shall surely produce a correct order when some keys are the same.

†In the extreme case, when all keys are equal, the pivot provides no separation at all. Obviously the pivot is the kth element for any k, and another approach is needed.

Table of Contents Go to Chapter 9

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1208.htm (44 of 44) [1.7.2001 19:22:21]

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/images/f7_1.gif

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/images/f7_1.gif [1.7.2001 19:22:26]