Data-Structures-And-Algorithms-Alfred-V-Aho

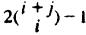
Data Structures and Algorithms: CHAPTER 10: Algorithm Design Techniques

a.Rewrite the odds calculation of Fig. 10.7 to take into account the fact that the first team has a probability p of winning any given game.

10.7b. If the Dodgers have won one game and the Yankees two, but the Dodgers have a .6 probability of winning any given game, who is more likely to win the World Series?

10.8

The odds calculation of Fig. 10.7 requires O(n2) space. Rewrite the algorithm to use only O (n) space.

10.10

Find a minimal triangulation for a regular octagon, assuming distances are Euclidean.

The paragraphing problem, in a very simple form, can be stated as follows: We are given a sequence of words w1, w2, . . . ,wk of lengths l1, l2, . . . ,lk, which we wish to break into lines of length L. Words are separated by blanks whose ideal width is b, but blanks can stretch or shrink if necessary (but without overlapping words), so that a line wi wi+1 ... wj has length exactly L. However, the penalty for stretching or shrinking is the magnitude of the total amount by which blanks are

10.11stretched or shrunk. That is, the cost of setting line wi wi+1 ... wj for j>i is (j-i) ½b'-b½, where b', the actual width of the blanks, is (L - li - li + 1-

...- lj)/(j-i). However, if j = k (we have the last line), the cost is zero unless b' < b, since we do not have to stretch the last line. Give a dynamic programming algorithm to find a least-cost separation of w1, w2, . . . ,wk into lines of length L. Hint. For i = k , k -1, . . ., 1, compute the least cost of setting wi , wi + 1, . . . ,wk.

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1210.htm (36 of 40) [1.7.2001 19:27:46]

Data Structures and Algorithms: CHAPTER 10: Algorithm Design Techniques

Suppose we are given n elements x1, x2,. . . ,xn related by a linear order x1 < x2 < · · · < xn, and that we wish to arrange these elements m in a binary search tree. Suppose that pi is the probability that a request to find an element will be for xi. Then for any given binary search tree,

10.12the average cost of a lookup is , where di is the depth of the node holding xi. Given the pi's, and assuming the xi's never change, we can find a binary search tree that minimizes the lookup cost. Find a dynamic programming algorithm to do so. What is the running time of your algorithm? Hint. Compute for all i and j the optimal lookup cost among all trees containing only xi, xi +1, . . . , xi +j-1, that is, the j elements beginning with xi.

Give an example where your algorithm does not produce an optimal answer, or show that no such example exists.

10.16Give a nonrecursive version of the tree search algorithm of Fig. 10.17.

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1210.htm (37 of 40) [1.7.2001 19:27:46]

Data Structures and Algorithms: CHAPTER 10: Algorithm Design Techniques

Consider a game tree in which there are six marbles, and players 1 and 2 take turns picking from one to three marbles. The player who takes the last marble loses the game.

c. Who wins the game if both play their best?

Develop a branch and bound algorithm for the TSP based on the idea that we shall begin a tour at vertex 1, and at each level, branch based on what node comes next in the tour (rather than on whether a

*10.18 particular edge is chosen as in Fig. 10.22). What is an appropriate lower bound estimator for configurations, which are lists of vertices 1, v1, v2, . . . that begin a tour? How does your algorithm behave on Fig.

10.21, assuming a is vertex 1?

A possible local search algorithm for the paragraphing problem is to allow local transformations that move the first word of one line to the

*10.19 previous line or the last word of a line to the line following. Is this algorithm locally optimal, in the sense that every locally optimal solution is a globally optimal solution?

10.20

If our local transformations consist of 2-opts only, are there any locally optimal tours in Fig. 10.21 that are not globally optimal?

Bibliographic Notes

There are many important examples of divide-and-conquer algorithms including the O(nlogn) Fast Fourier Transform of Cooley and Tukey [1965], the O(nlognloglogn) integer multiplication algorithm of Schonhage and Strassen [1971], and the O(n2.81) matrix multiplication algorithm of Strassen [1969]. The O(n1.59) integer multiplication algorithm is from Karatsuba and Ofman [1962]. Moenck and Borodin [1972] develop several efficient divide-and-conquer algorithms for modular

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1210.htm (38 of 40) [1.7.2001 19:27:46]

Data Structures and Algorithms: CHAPTER 10: Algorithm Design Techniques

arithmetic and polynomial interpolation and evaluation.

Dynamic programming was popularized by Bellman [1957]. The application of dynamic programming to triangulation is due to Fuchs, Kedem, and Uselton [1977]. Exercise 10.11 is from Knuth [1981]. Knuth [1971] contains a solution to the optimal binary search tree problem in Exercise 10.12.

Lin and Kernighan [1973] describe an effective heuristic for the traveling salesman problem.

See Aho, Hopcroft, and Ullman [1974] and Garey and Johnson [1979] for a discussion of NP-complete and other computationally difficult problems.

1. In the towers of Hanoi case, the divide-and-conquer algorithm is really the same as the one given initially.

†In what follows, we take all subscripts to be computed modulo n. Thus, in Fig. 10.8, vi and vi+1 could be v6 and v0, respectively, since n = 7.

†Remember that the table of Fig. 10.11 has rows of 0's below those shown.

‡By "to the right" we mean in the sense of a table that wraps around. Thus, if we are at the rightmost column, the column "to the right" is the leftmost column.

†In fact, we should be careful what we mean by "shortest path" when there are negative edges. If we allow negative cost cycles, then we could traverse such a cycle repeatedly to get arbitrarily large negative distances, so presumably we want to restrict ourselves to acyclic paths.

†Incidentally, some of the other things good chessplaying programs do are:

1.Use heuristics to eliminate from consideration certain moves that are unlikely to be good. This helps expand the tree to more levels in a fixed time.

2.Expand "capture chains", which are sequences of capturing moves beyond the last level to which the tree is normally expanded. This helps estimate the relative material strength of positions more accurately.

3.Prune the tree search by alpha-beta pruning, as discussed later in this section.

‡We should not imply that only "games" can be solved in this manner. As we shall see in subsequent examples, the "game" could really represent the solution to a

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1210.htm (39 of 40) [1.7.2001 19:27:46]

Data Structures and Algorithms: CHAPTER 10: Algorithm Design Techniques

practical problem.

†Note that we need not consider all n! permutations, since the starting point of a tour is immaterial. We may therefore consider only those permutations that begin with 1.

†The rules for constructing the search tree will be seen to eliminate any set of constraints that cannot yield any tour, e.g., because three edges adjacent to one node are required to be in the tour.

†An alternative is to use a heuristic to obtain a good solution using the constraints required for each child. For example, the reader should be able to modify the greedy TSP algorithm to respect constraints.

‡We could start with some heuristically found solution, say the greedy one, although that would not affect this example. The greedy solution for Fig. 10.21 has cost 21.

†Do not be fooled by the picture of Fig. 10.25. True, if lengths of edges are distances in the plane, then the dashed edges in Fig. 10.25 must be longer than those they replace. In general, however, there is no reason to assume the distances in Fig. 10.25 are distances in the plane, or if they are, it could have been (A B) and (C, D) that crossed, not (a C) and (B, D).

Table of Contents Go to Chapter 11

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1210.htm (40 of 40) [1.7.2001 19:27:46]

Data Structures and Algorithms: CHAPTER 11: Data Structures and Algorithms for External Storage

Data Structures and Algorithms for External Storage

We begin this chapter by considering the differences in access characteristics between main memory and external storage devices such as disks. We then present several algorithms for sorting files of externally stored data. We conclude the chapter with a discussion of data structures and algorithms, such as indexed files and B-trees, that are well suited for storing and retrieving information on secondary storage devices.

11.1 A Model of External Computation

In the algorithms discussed so far, we have assumed that the amount of input data is sufficiently small to fit in main memory at the same time. But what if we want to sort all the employees of the government by length of service or store all the information in the nation's tax returns? In such problems the amount of data to be processed exceeds the capacity of the main memory. Most large computer systems have on-line external storage devices, such as disks or mass storage devices, on which vast quantities of data can be stored. These on-line storage devices, however, have access characteristics that are quite different from those of main memory. A number of data structures and algorithms have been developed to utilize these devices more effectively. This chapter discusses data structures and algorithms for sorting and retrieving information stored in secondary memory.

Pascal, and some other languages, provide the file data type, which is intended to represent data stored in secondary memory. Even if the language being used does not have a file data type, the operating system undoubtedly supports the notion of files in secondary memory. Whether we are talking about Pascal files or files maintained by the operating system directly, we are faced with limitations on how files may be accessed. The operating system divides secondary memory into equalsized blocks. The size of blocks varies among operating systems, but 512 to 4096 bytes is typical.

We may regard a file as stored in a linked list of blocks, although more typically the operating system uses a tree-like arrangement, where the blocks holding the file are leaves of the tree, and interior nodes each hold pointers to many blocks of the file. If, for example, 4 bytes suffice to hold the address of a block, and blocks are 4096 bytes long, then a root block can hold pointers to up to 1024 blocks. Thus, files of up to 1024 blocks, i.e., about four million bytes, could be represented by a root

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1211.htm (1 of 34) [1.7.2001 19:28:20]

Data Structures and Algorithms: CHAPTER 11: Data Structures and Algorithms for External Storage

block and blocks holding the file. Files of up to 220 blocks, or 232 bytes could be represented by a root block pointing to 1024 blocks at an intermediate level, each of which points to 1024 leaf blocks holding a part of the file, and so on.

The basic operation on files is to bring a single block to a buffer in main memory; a buffer is simply a reserved area of main memory whose size is the same as the size of a block. A typical operating system facilitates reading the blocks in the order in which they appear in the list of blocks that holds the file. That is, we initially read the first block into the buffer for that file, then replace it by the second block, which is written into the same buffer, and so on.

We can now see the rationale behind the rules for reading Pascal files. Each file is stored in a sequence of blocks, with a whole number of records in each block. (Space may be wasted, as we avoid having one record split across block boundaries.) The read-cursor always points to one of the records in the block that is currently in the buffer. When that cursor must move to a record not in the buffer, it is time to read the next block of the file.

Similarly, we can view the Pascal file-writing process as one of creating a file in a buffer. As records are "written" into the file, they are placed in the buffer for that file, in the position immediately following any previously placed records. When the buffer cannot hold another complete record, the buffer is copied into an available block of secondary storage and that block is appended to the end of the list of blocks for that file. We can now regard the buffer as empty and write more records into it.

The Cost Measure for Secondary Storage Operations

It is the nature of secondary storage devices such as disks that the time to find a block and read it into main memory is large compared with the time to process the data in that block in simple ways. For example, suppose we have a block of 1000 integers on a disk rotating at 1000 rpm. The time to position the head over the track holding this block (seek time) plus the time spent waiting for the block to come around to the head (latency time) might average 100 milliseconds. The process of writing a block into a particular place on secondary storage takes a similar amount of time. However, the machine could typically do 100,000 instructions in those 100 milliseconds. This is more than enough time to do simple processing to the thousand integers once they are in main memory, such as summing them or finding their maximum. It might even be sufficient time to quicksort the integers.

When evaluating the running time of algorithms that operate on data stored as

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1211.htm (2 of 34) [1.7.2001 19:28:20]

Data Structures and Algorithms: CHAPTER 11: Data Structures and Algorithms for External Storage

files, we are therefore forced to consider as of primary importance the number of times we read a block into main memory or write a block onto secondary storage. We call such an operation a block access. We assume the size of blocks is fixed by the operating system, so we cannot appear to make an algorithm run faster by increasing the block size, thereby decreasing the number of block accesses. As a consequence, the figure of merit for algorithms dealing with external storage will be the number of block accesses. We begin our study of algorithms for external storage by looking at external sorting.

11.2 External Sorting

Sorting data organized as files, or more generally, sorting data stored in secondary memory, is called "external" sorting. Our study of external sorting begins with the assumption that the data are stored on a Pascal file. We show how a "merge sorting" algorithm can sort a file of n records with only O(log n) passes through the file; that figure is substantially better than the O(n) passes needed by the algorithms studied in Chapter 8. Then we consider how utilization of certain powers of the operating system to control the reading and writing of blocks at appropriate times can speed up sorting by reducing the time that the computer is idle, waiting for a block to be read into or written out of main memory.

Merge Sorting

The essential idea behind merge sort is that we organize a file into progressively larger runs, that is, sequences of records r1, . . . , rk, where the key of ri is no greater

than the key of ri+1 for 1 £ i < k. We say a file r1, . . . ,rm of records is organized into

runs of length k if for all i ³ 0 such that ki £ m, rk(i-l)+l, rk(i-1)+2, . . . ,rki is a run of length k, and furthermore if m is not divisible by k, and m = pk+q, where q<k, then the sequence of records rm-q+1, rm-q+2, . . . ,rm, called the tail, is a run of length q. For example, the sequence of integers shown in Fig. 11.1 is organized into runs of length 3 as shown. Note that the tail is of length less than 3, but consists of records in sorted order, namely 5, 12.

Fig. 11.1. File with runs of length three.

The basic step of a merge sort on files is to begin with two files, say f1 and f2, organized into runs of length k. Assume that

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1211.htm (3 of 34) [1.7.2001 19:28:20]

Data Structures and Algorithms: CHAPTER 11: Data Structures and Algorithms for External Storage

1.the numbers of runs, including tails, on f1 and f2 differ by at most one,

2.at most one of f1 and f2 has a tail, and

3.the one with a tail has at least as many runs as the other.

Then it is a simple process to read one run from each of f1 and f2, merge the runs and append the resulting run of length 2k onto one of two files g1 and g2, which are being organized into runs of length 2k. By alternating between g1 and g2, we can arrange that these files are not only organized into runs of length 2k, but satisfy (l), (2), and

(3) above. To see that (2) and (3) are satisfied it helps to observe that the tail among the runs of f1 and f2 gets merged into (or perhaps is) the last run created.

We begin by dividing all n of our records into two files f1 and f2, as evenly as possible. Any file can be regarded as organized into runs of length 1. Then we can merge the runs of length 1 and distribute them into files g1 and g2, organized into runs of length 2. We make f1 and f2 empty, and merge g1 and g2 into f1 and f2, which will then be organized into runs of length 4. Then we merge f1 and f2 to create g1 and g2 organized into runs of length 8, and so on.

After i passes of this nature, we have two files consisting of runs of length 2i. If 2i ³ n, then one of the two files will be empty and the other will contain a single run of length n, i.e., it will be sorted. As 2i ³ n when i ³ logn, we see that [logn] passes suffice. Each pass requires the reading of two files and the writing of two files, all of length about n/2. The total number of blocks read or written on a pass is thus about 2n/b, where b is the number of records that fit on one block. The number of block reads and writes for the entire sorting process is thus O((nlogn)/b), or put another way, the amount of reading and writing is about the same as that required by making O(logn) passes through the data stored on a single file. This figure is a large improvement over the O(n) passes required by many of the sorting algorithms discussed in Chapter 8.

Figure 11.2 shows the merge process in Pascal. We read two files organized into runs of length k and write two files organized into runs of length 2k. We leave to the reader the specification of an algorithm, following the ideas above, that uses the procedure merge of Fig. 11.2 logn times to sort a file of n records.

procedure merge ( k: integer; { the input run length } f1, f2, g1, g2: file of recordtype );

var

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1211.htm (4 of 34) [1.7.2001 19:28:20]

Data Structures and Algorithms: CHAPTER 11: Data Structures and Algorithms for External Storage

outswitch: boolean; { tells if writing g1 (true) or g2 (false) } winner: integer; { selects file with smaller key in current record } used: array [1..2] of integer; { used[j] tells how many

records have been read so far from the current run of file fj } fin: array [1..2] of boolean; { fin[j] is true if we have

finished the run from fj - either we have read k records, or reached the end of the file of fj }

current: array [1..2] of recordtype; { the current records from the two files }

procedure getrecord ( i: integer ); { advance file fi, but

not beyond the end of the file or the end of the run. Set fin[i] if end of file or run found }

begin

used[i] := used[i] + 1; if (used[i] = k) or

(i = 1) and eof(f 1) or

(i = 2) and eof(f 2) then fin[i]:= true else if i = 1 then read(f 1, current[1]) else read(f 2, current[2])

end; { getrecord }

begin { merge }

outswitch := true; { first merged run goes to g 1 } rewrite(g 1); rewrite(g 2);

reset(f 1); reset(f 2);

while not eof(f 1) or not eof(f 2) do begin

{ merge two file } { initialize }

used[1] := 0; used[2] := 0; fin[1] := false; fin[2] := false; getrecord(1); getrecord(2);

while not fin[1] or not fin[2] do begin { merge two runs

}

{ select winner }

if fin[1] then winner : = 2

{f 2 wins by "default" - run from f 1 exhausted } else if fin[2] then winner := 1

{f 1 wins by default }

else { neither run exhausted }

http://www.ourstillwaters.org/stillwaters/csteaching/DataStructuresAndAlgorithms/mf1211.htm (5 of 34) [1.7.2001 19:28:20]